 |
Покажи тринадцать палочек. Сколько это десятков и сколько еще отдельных палочек?
|
|
|
|
2) на принцип образования натурального ряда чисел:
Сделай рисунок к задаче и реши ее устно. «В городе было 10 кинотеатров. Построили еще 1. Сколько кинотеатров стало в городе?»
Уменьши на 1: 16, 11, 13, 20
Увеличь на 1: 19, 18, 14, 17
Найди значение выражения: 10 + 1; 14 + 1; 18 - 1; 20 - 1.
(Во всех случаях можно ссылаться на то, что добавление 1 ведет к получению числа последующего, а уменьшение на 1 — к получению числа предыдущего.)
3) на поместное значение цифры в записи числа:
Что обозначает каждая цифра в записи числа: 15, 13, 18, 11, 10, 20?
(В записи числа 15 цифра 1 обозначает количество десятков, а цифра 5 — количество единиц. В записи числа 20 цифра 2 обозначает, что в числе 2 десятка, а цифра 0 обозначает, что в первом разряде единиц нет.)
4) на место числа в ряду чисел:
Вставь пропущенные числа: 12.........16 17... 19 20
Вставь пропущенные числа: 20... 18 17.........13... 11
(При выполнении задания ссылаются на порядок чисел при счете.)
5) на разрядный (десятичный) состав:
10 + 3 =... 13-3 =... 13-10 =...
12= 10 +... 15 =...+ 5
При выполнении задания ссылаются на разрядную (десятичную) модель числа из десятка (пучка палочек) и единиц (отдельных палочек),
6) на сравнение чисел второго десятка:
Какое из чисел больше: 13 или 15? 14 или 17? 18 или 14? 20 или 12?
При выполнении задания можно сравнивать две модели чисел из палочек (количественная модель), или ссылаться на порядок следования чисел при счете (меньшее число называют при счете раньше), или опираться на процесс присчитывания и отсчитывания (присчитывая к 13 две единицы получим 15, значит 15 больше, чем 13).
Сравнивая числа второго десятка с однозначными числами, следует ссылаться на то, что все однозначные числа меньше, чем двузначные:
Назови самое большое и самое маленькое из этих чисел: 12 6 18 10 7 20.
|
|
|
При сравнении чисел второго десятка удобно пользоваться линейкой.

I I I I I I I I I I I I I I I I I I I I I I I I I I
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
Сравнивая длины соответствующих отрезков, ребенок наглядно определяет постановку знака сравнения: 17 < 19.
Числа первой сотни
Десять десятков — это сотня. Числа от 11 до 100 называют числами первой сотни. Все числа первой сотни — двузначные.
Двузначные числа записывают двумя цифрами: 37, 45, 64, 40. Первая цифра справа в записи двузначного числа называется цифрой первого разряда или разряда единиц, вторая цифра справа — цифрой второго разряда или разряда десятков.
Целые десятки (10 20 30 40 50 60 70 80 90) иногда именуются разрядными числами.
Читают двузначные числа слева направо. Для чисел 21 — 100 порядок называния составляющих их разрядных чисел и порядок записи совпадает: 21 (два-дцать один)
Понятие «разряд» является базовым для образования чисел первой сотни.
Разрядный состав — выделение разрядных чисел в двузначном числе:

На основе разрядного состава рассматриваются случаи разрядного сложения и вычитания: 30 + 4 34-4 34-30
При нахождении значений этих выражений ссылаются на разрядный состав двузначных чисел: число 34 состоит из 30 и 4. Вычитая 30 получаем 4.
Разрядные слагаемые — сумма разрядных чисел двузначного числа:
47 = 40 + 7 68 - 60 + 8
Десятичный состав — выделение десятков и единиц в двузначном числе:
26 — это 2 дес. и 6 ед.
Схема десятичного состава:

На основе схемы десятичного состава можно рассмотреть такие случаи сложения и вычитания:
26-6 26-20 26- 10 26- 16 20 + 6
При нахождении значения этих выражений ссылаются на десятичный состав (десятичную схему) двузначного числа: вычитая из числа 26 число 16 (1 десяток и 6 единиц) получаем 1 десяток. Для наглядности ребенок прикрывает вычитаемое рукой на схеме. В дальнейшем это действие ребенок выполняет мысленно и сразу называет и пишет ответ. Использование десятичной схемы двузначного числа значительно облегчает вычислительную деятельность детям, которым вычисления «в уме» даются трудно. Например, десятичная схема числа 57 дает возможность без применения каких-либо еще вспомогательных приемов вычислений решить следующие примеры:
|
|
|
| 57-10 | 57-20 | 57-30 | |
| 57-40 | 57-50 | 50 +7 | |
| 57-17 | 57-27 | 57-37 | |
| 57-47 | |||
а также легко справиться со случаями вида: 57 + 2; 57 + 3; 57 + 10 и т. п., используя прием «десятки к десяткам, а единицы к единицам».
При изучении нумерации двузначных чисел рассматривают также случаи сложения и вычитания, базирующиеся на принципе построения последовательности натуральных чисел: 43 + 1; 43 - 1; 40 + 1; 40 - 1.
При нахождении значения этих выражений/ссылаются на принцип построения натурального ряда чисел: прибавляя к числу 1, получаем число следующее (последующее). Вычитая из числа 1, получаем число предыдущее.
Приведем основные виды заданий, выполняемых детьми при изучении чисел первой сотни:
1) на способ образования чисел первой сотни:
Назови число, в котором 1 дес. 9 ед., 2 дес. 7 ед., 9 дес. 2 ед.
Запиши числа, в которых 3 дес. 7 ед., 7 дес. 3 ед., 7 дес. 0 ед.
2) на соотнесение количественной модели, названия и записи числа:
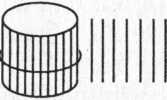
Сколько кубиков на каждом рисунке?

Прочитай и запиши число по модели:
| Десятки | Единицы |
| 
|
3) на принцип образования натурального ряда чисел:
Уменьши на 1: 20, 47, 32, 50, 70
Увеличь на 1: 19, 28, 44, 67, 40, 90
Найди значение выражения: 50 + 1; 44 + 1; 68 — 1; 90 — 1.
Во всех случаях можно ссылаться на то, что добавление 1 ведет к получению числа последующего, а уменьшение на 1 — к получению числа предыдущего.
4) на поместное значение цифры в записи числа:
Что обозначает каждая цифра в записи числа: 72, 20, 70, 27? (В записи числа 72 цифра 7 обозначает количество десятков, а цифра 2 — количество единиц. В записи числа 20 цифра 2 обозначает, что в числе 2 десятка, а цифра 0 обозначает, что в первом разряде единиц нет.)
5) на место числа в ряду чисел:
Вставь пропущенные числа:
40, 41... 43......... 47...... 50
Вставь пропущенные числа:
70, 69............ 64...... 61...
При выполнении задания ссылаются на порядок чисел при счете.
6) на разрядный состав:
|
|
|
20 + 3 = 23 23 - 3 =... 23-20 =...
37 = 30 + 7 37 - 30 =... 37 - 7 =...
При выполнении задания ссылаются на разрядную модель числа из десятков и единиц.
7) на сравнение чисел первой сотни:
Какое из чисел больше: 23 или 32? 44 или 47? 28 или 54? 20 или 4?
При выполнении задания можно сравнивать две модели чисел из палочек (количественная модель), или ссылаться на порядок следования чисел при счете (меньшее число называют при счете раньше), или опираться на процесс присчитывания и отсчитывания (присчитывая к 44 три единицы получим 47, значит 47 больше, чем 44).
Более соответствующим данному этапу изучения нумерации считается способ сравнения чисел с опорой на разрядный состав. При этом сравнивать числа начинают со старших разрядов: в числе 23 — два десятка, а в числе 32 — три десятка, значит 32 > 23. Если количество десятков одинаковое, то сравнивают цифры разряда единиц: в числе 44 и числе 47 по 4 десятка, сравним разряд единиц — 7 больше, чем 4, значит 47 > 44.
Сравнивая двузначные числа с однозначными числами, следует ссылаться на то, что все однозначные числа меньше, чем двузначные.
При сравнении чисел вида:
| < > = |
следует ссылаться на порядок следования чисел при счете: следующее число всегда больше, чем предыдущее.
Для наглядного сравнения чисел первой сотни можно использовать портновскую ленту.
8) на десятичный состав двузначных чисел:
Сколько десятков в числе 56, 78, 92?
Комплексное задание на нумерацию двузначных чисел включает полную характеристику заданного числа.
Что можно рассказать о числе 33? (57, 62)
(Это число двузначное, записано с помощью двух цифр. Вэтом числе 3 десятка и 3 единицы или 3 единицы II разряда и 3 единицы I разряда; при счете его называют после числа 32 и перед числом 34 (или — его соседи 32 и 34); оно больше, чем число 30 и меньше, чем число 40; его можно представить в виде суммы 30 и 3.)
Завершает изучение чисел первой сотни знакомство с числом 100.
Десять десятков — это сотня.
Число 100 завершает изучение чисел первой сотни.
Сотня (100) — первое трехзначное число в ряду натуральных чисел.
Сотня — наименьшее трехзначное число.
|
|
|
Сотня — новая счетная единица в десятичной системе счисления.
В записи числа 100 цифра 1 обозначает, что в ИТ разряде (разряде сотен) — одна единица, а разрядах десятков и единиц нули означают, что в этих разрядах нет значащих цифр.
Числа первой тысячи
Числа первой тысячи образуют первый класс — класс единиц.
Десять десятков — это сотня. Десять сотен — это тысяча. Числа от 101 до 1000 называют числами первой тысячи. Все числа первой тысячи — трехзначные.
Трехзначные числа записывают тремя цифрами: 537,455,164,340. Первая цифра справа в записи трехзначного числа называется цифрой первого разряда или разряда единиц, вторая цифра справа — цифрой второго разряда или разряда десятков, третья цифра справа — цифрой третьего разряда или разряда сотен.
Целые сотни (100 200 300 400 500 600 700 800 900) иногда именуются «разрядными числами».
1 сотня — сто 6 сотен — шестьсот
2 сотни — двести 7 сотен — семьсот
3 сотни — триста 8 сотен — восемьсот
4 сотни — четыреста 9 сотен — девятьсот
5 сотен — пятьсот 10 сотен — тысяча
Читают трехзначные числа слева направо. Для чисел 101—1000 порядок называния составляющих их разрядных чисел и порядок записи совпадает: 321— триста двадцать один.
Понятие «разряд» является базовым для образования чисел первой тысячи. Все числа первой тысячи содержат три разряда.
Разрядный состав — выделение разрядных чисел в трехзначном числе:

На основе разрядного состава рассматриваются случаи разрядного сложения и вычитания:
| 400+30 | 340-40 |
| 534-34 | 534-30 |
| 672-600 | 243-3 |
При нахождении значений этих выражений ссылаются на разрядный состав трехзначных чисел: число 534 состоит из 500, 30 и 4. Вычитая 30, получаем 504.
Разрядные слагаемые — сумма разрядных чисел трехзначного числа:
247 = 200 + 40 + 7 968 = 900 + 60 + 8
Десятичный состав — выделение десятков и единиц в трехзначном числе:
326 — это 32 дес. и 6 ед.; 480 — это 48 дес. и 0 ед.
При изучении нумерации трехзначных чисел рассматривают также случаи сложения и вычитания, базирующиеся на принципе построения последовательности натуральных чисел:
| 443+1 | 443-1 | 640+1 | 640-1 |
| 599+1 | 700-1 | 999+1 | 1000-1 |
При нахождении значения этих выражений, ссылаются на принцип построения натурального ряда чисел: прибавляя к числу 1, получаем число следующее (последующее). Вычитая из числа 1, получаем число предыдущее.
Приведем основные виды заданий, выполняемых детьми при изучении чисел первой тысячи:
1) на способ образования чисел первой тысячи:
Назови число, в котором 3 сот. 1 дес. 9 ед.; 1 сот. 2 дес. 7 ед.; 6 сот. 9 дес. 2 ед.
Запиши числа, в которых 3 сот. 0 дес. 7 ед.; 1 сот. 7 дес. 3 ед.; 5 сот. 7дес. 0 ед.
Сколько всего палочек, если есть: 2 пучка по 100 палочек, 4 пучка по 10 палочек и 5 палочек?
|
|
|
2) на соотнесение количественной модели, названия и записи числа:
Как с помощью палочек изобразить в таблице числа: двести тридцать шесть? триста пятьдесят?
Прочитай числа, записанные в таблице:
| Сотни | Десятки | Единицы |
3) на принцип образования натурального ряда чисел:
Какое число при счете следует за числом 199? 999? Какое число предшествует числу 840? 1000?
Увеличь на 1:
199; 287; 444; 670; 405; 901
Найди значение выражения:
500 — 1; 744 + 1; 689 + 1; 990 - 1
Во всех случаях можно ссылаться на то, что добавление 1 ведет к получению числа последующего, а уменьшение на 1 — к получению числа предыдущего.
4) на поместное значение цифры в записи числа:
Что обозначает каждая цифра в записи чисел: 894, 809, 408, 900? (Взаписи числа 894цифра 8 обозначает количество сотен, цифра 9 обозначает количество десятков, а цифра 4 — количество единиц. Взаписи числа 900 цифра 9 обозначает, что в числе 9 сотен, а цифра 0 в разрядах десятков и единиц обозначает, что в первом и втором разрядах единиц нет.)
Сколько всего цифр использовано для записи каждого числа: 578, 785. Используя эти же цифры запиши другие трехзначные числа.
5) на место числа в ряду чисел:
Во Дворце спорта в одном ряду были свободны места с 231 по 240. Назови, какие места свободны.
При выполнении задания ссылаются на порядок чисел при счете.
6) на разрядный состав:
Замени числа суммой по образцу:
195 = 100 + 90 + 5 657 =... 304 =.....
При выполнении задания ссылаются на разрядную модель числа из сотен, десятков и единиц.
Заполни пропуски, чтобы равенства были верными: 999 =... + 90 + 9 564 = 500 +... + 4
Вычисли:
400 + 80-1; 978 - 8 - 1; 500 + 99 + 1; 750 — 50+1
Эти задания представляют собой комбинированные примеры на разрядный состав и принцип построения натурального ряда чисел.
При вычислениях сначала применяется разрядное сложение или вычитание, а затем присчитывание или отсчитывание.
7) на сравнение чисел первой тысячи:
Какое из чисел больше: 709 или 789; 578 или 571; 499 или 500; 300 или 150?
При выполнении задания можно сравнивать две модели чисел из косточек на счетах (количественная модель), или ссылаться на порядок следования чисел при счете (меньшее число называют при счете раньше), или опираться на процесс присчитывания и отсчитывания (присчитывая к 571 семь единиц получим 578, значит, 578 больше, чем 571).
Более соответствующим данному этапу изучения нумерации считается способ сравнения чисел с опорой на разрядный состав. Сравнивать числа начинают со старших разрядов: в числе 300 — три сотни, а в числе 150 — одна сотня, значит 300 > 150. Если количество сотен одинаковое, то сравнивают цифры разряда десятков, а если и они равны, то сравниваются цифры разряда единиц: в числе 709 и числе 789 по 7 сотен, сравним разряд десятков — в первом числе в разряде десятков 0 единиц, во втором числе в разряде десятков 8 единиц, значит 789 > 709.
Сравни числа: 35 и 355; 7 и 107.
Сравнивая трехзначные числа с однозначными и двузначными числами, следует ссылаться на то, что все однозначные и двузначные числа меньше, чем трехзначные.
При сравнении чисел вида:
| < > = |
следует ссылаться на порядок следования чисел при счете: следующее число всегда больше, чем предыдущее.
8) на десятичный состав двузначных чисел:
Отсчитывай от двухсот по 10 до 80.
Присчитывай к двумстам по 100 до тысячи.
Сколько всего десятков в числах 150, 270, 400? (Десятков 15, 27, 40.)
Запиши 5 чисел, каждое из которых содержит 37 десятков. Сколько таких чисел можно записать? (370, 371, 372, 373, 374,... Всего чисел, содержащих 37десятков, десять. Число 380 уже содержит 38 десятков.)
9) на соотношения между разрядами:
Сколько единиц составляют 5 сот., 2 сот., 24 дес?
В прыжке с шестом спортсмен взял высоту 600 см. Вырази эту высоту в метрах.
1 сот. = 10 дес. =...ед.; 10 сот. = 100 дес. =... ед.
Комплексное задание на нумерацию двузначных чисел включает полную характеристику заданного числа:
Что можно рассказать о числе 335? (Это число трехзначное, записано с помощью трех цифр. В этом числе 3 сотни, 3 десятка и 5 единиц или 3 единицы Ill-го разряда, 3 единицы 11-го разряда и 5 единиц 1-го разряда; при счете его называют после числа 334 и перед числом 336 (или — его соседи 334 и 336); оно больше, чем число 330 и меньше, чем число 340; его можно представить в виде суммы 300, 30 и 5.)
Завершает изучение чисел первой сотни знакомство с числом 1000. Десять сотен — это тысяча.
Число 1000 завершает изучение трехзначных чисел. Тысяча (1000) — первое четырехзначное число в ряду натуральных чисел.
Тысяча — наименьшее четырехзначное число.
Тысяча — новая счетная единица в десятичной системе счисления.
В записи числа 1000 цифра 1 обозначает, что в IV разряде (разряде тысяч) — одна единица, а разрядах сотен, десятков и единиц нули означают, что в этих разрядах нет значащих цифр.
4. Многозначные числа
Многозначными считают числа больше тысячи. Многозначные числа — это числа класса тысяч и класса миллионов. Многозначные числа образуются, называются, записываются с опорой не только на понятие разряда, но и на понятие класса.
Класс объединяет три разряда.
Класс единиц — единицы, десятки сотни. Это — первый класс.
Класс тысяч — единицы тысяч, десятки тысяч, сотни тысяч. Это — второй класс. Единица этого класса — тысяча.
Класс миллионов — единицы миллионов, десятки миллионов, сотни миллионов. Это — третий класс. Единица этого класса — миллион.
Таблица разрядов I класса:
| Сотни | Десятки | Единицы |
| единицы III разряда | Единицы II разряда | Единицы 1 разряда |
| В таблице записано число 257. Таблица разрядов II класса: | ||
| Сотни тысяч | Десятки тысяч | Единицы тысяч |
| Единицы VI разряда | Единицы V разряда | Единицы IV разряда |
| 2 сот. тыс. | 5 дес. тыс. | 7 ед. тыс. |
| В таблице записано число 257 ООО. Таблица разрядов III класса: | ||
| Сотни миллионов | Десятки миллионов | Единицы миллионов |
| Единицы IX разряда | Единицы VIII разряда | Единицы VII разряда |
| 2 сот. млн | 7 дес. млн | 5 ед. млн |
В таблице записано число 275 000 000.
Многозначные числа образуют второй класс — класс тысяч и третий класс — класс миллионов.
Десять сотен — это тысяча. Числа от 1001 до 1 000 000 называют числами класса тысяч.
Числа класса тысяч — это четырех-, пяти- и шестизначные числа.
Четырехзначные числа записывают четырьмя цифрами: 1537, 7455, 3164, 3401. Первая цифра справа в записи четырехзначного числа называется цифрой первого разряда или разряда единиц, вторая цифра справа — цифрой второго разряда или разряда десятков, третья цифра справа — цифрой третьего разряда или разряда сотен, четвертая цифра справа — цифрой четвертого разряда или разряда тысяч.
Цифра пятого разряда — это цифра десятков тысяч, цифра шестого разряда — это цифра сотен тысяч.
Целые тысячи: 1 000, 2000,3000,4000,5000,6000,7000,8000,9000.
Читают многозначные числа слева направо. Для чисел 1001 и далее порядок называния составляющих их разрядных чисел и порядок записи совпадает: 4 321— четыре тысячи триста двадцать один; 346 456 — триста сорок шесть тысяч четыреста пятьдесят шесть.
Правило чтения многозначных чисел: многозначные числа читают слева направо. Сначала разбивают число на классы, отсчитывая справа по три цифры. Чтение начинают с единиц старших классов (слева). Единицы старших классов читают сразу как трехзначное число, добавляя затем название класса. Единицы I класса читают без добавления названия класса.
Например: 1 234 456 — один миллион двести тридцать четыре тысячи четыреста пятьдесят шесть.
Если какой-то класс в записи числа не содержит значащих цифр, его при чтении пропускают.
Например: 123 000 324 — сто двадцать три миллиона триста двадцать четыре.
Понятие «класс» является базовым для образования многозначных чисел. Все многозначные числа содержат два и более классов. Класс объединяет три разряда (единицы, десятки и сотни).
| II класс — класс тысяч | 1 класс — класс единиц | ||||
| Сотни тысяч | Десятки тысяч | Единицы тысяч | Сотни | Десятки | Единицы |
На письме при записи многозначного числа принято делать разрядку между классами: 345 674, 23 456, 101 405,12 345 567.
Правило записи многозначных чисел: многозначные числа записывают по классам, начиная с высших. Чтобы записать цифрами число, например, двенадцать миллионов четыреста пятьдесят тысяч семьсот сорок два, поступают так: записывают группами единицы каждого названного класса, отделяя один класс от другого небольшим промежутком (разрядкой): 12 450 742.
Классовый состав — выделение «классовых чисел» (классовых составляющих) в многозначном числе.
Например: 123 456 = 123 000 + 456
34 123 345 - 34 000 000 + 123 000 + 345
Разрядный состав — выделение разрядных чисел в многозначном числе: _
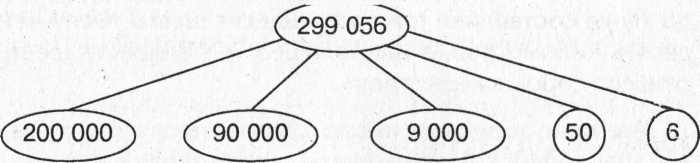
На основе разрядного состава рассматриваются случаи разрядного сложения и вычитания:
400 000 + 3 000 20 534 - 34 340 000 - 40 000
534 000 - 30 000 672 000 - 600 000 24 000 + 300
При нахождении значений этих выражений ссылаются на разрядный состав трехзначных чисел: число 340 000 состоит из 300 000 и 40 000. Вычитая 40 000 получаем 300 000.
Разрядные слагаемые—сумма разрядных чисел многозначного числа:
247 000 - 200 000 + 40 000 + 7 000
968 460 ч 900 000 + 60 000 + 8 000 + 400 + 60
Десятичный состав — выделение десятков и единиц в многозначном числе: 234 000 это 23 400 дес. или 2 340 сот.
При изучении нумерации многозначных чисел рассматривают также случаи сложения и вычитания, базирующиеся на принципе построения последовательности натуральных чисел:
443 999+ 1 20 443- 1 640 000+ 1 640 000-1
10 599 + 1 700 000 - 1 99 999 + 1 100 000 - 1
При нахождении значения этих выражений, ссылаются на принцип построения натурального ряда чисел: прибавляя к числу 1, получаем число следующее (последующее). Вычитая из числа 1, получаем число предыдущее.
Приведём основные виды заданий, выполняемых детьми при изучении многозначных чисел:
1) на чтение и запись многозначных чисел:
Разбей число на классы, скажи, сколько в нем единиц каждого класса, а потом прочитай число:
7300 29608 305220 400400 90060 7340 29680 305020 400004 60090
При выполнении задания следует воспользоваться правилом чтения многозначных чисел.
Запиши и прочитай числа, в которых: а) 30 ед. второго класса и 870 ед. первого класса; б) 8 ед. второго класса и 600 ед. первого класса; в) 4 ед. второго класса и 0 ед. первого класса.
При выполнении задания следует воспользоваться таблицей разрядов и классов.
Запиши числа цифрами: «Наименьшее расстояние от Земли до Луны составляет триста пятьдесят шесть тысяч четыреста десять километров, а наибольшее — четыреста шесть тысяч семьсот сорок километров».
Ученики записали число девять тысяч сорок так: 940, 900 040, 9 040. Объясни, какая запись правильная.
При выполнении заданий следует воспользоваться правилом записи многозначных чисел.
2) на разрядный и классовый состав многозначных чисел:
Замени данные числа суммой по образцу: 108 201 = 108 000 + 201
360 400 =... +... 50 070 =... +... 9 007 =... +...
Задание на классовый состав многозначного числа.
Замени каждое число суммой разрядных слагаемых:
205 000 =... +... 640 000 =... +...
Вычисли: 200 000 + 90 000 + 9 000 4 000 + 8 000
299 000 - 200 000 408 000 - 8 000
Сколько единиц каждого разряда в числе 395 028, в числе 602 023? Сколько единиц каждого класса в этих числах?
При выполнении заданий используют схему разрядного состава многозначных чисел.
3) на принцип образования натурального ряда чисел:
Найди значения выражений: 99 999 + 1 30 000 — 1
100 000- 1 699 999 + 1
Во всех случаях можно ссылаться на то, что добавление 1 ведет к получению числа последующего, а уменьшение на 1 — к получению числа предыдущего.
4) на порядок следования чисел в натуральном ряду:
У трех тракторов такие заводские номера: 250 000, 249 999, 250 001. Какой из них сошел с конвейера первым? Вторым? Третьим?
Запиши все шестизначные числа, которые больше числа 999 996.
5) на поместное значение цифры в записи числа:
Что обозначает цифра 2 в записи каждого числа: 2, 20, 200, 2 000, 20 000, 200 000? Объясни, как меняется значение цифры 2 в записи числа при изменении ее места.
Что обозначает каждая цифра в записи чисел: 140 401, 308 000, 70 050?
(В записи числа 140 401 цифра 4, стоящая на третьем месте справа, обозначает количество сотен, цифра 4, стоящая на пятом месте справа, обозначает количество десятков тысяч. Цифра 1, стоящая на первом месте справа, обозначает количество единиц в числе, а цифра 1, стоящая на шестом месте справа, — количество сотен тысяч. Цифра 0, стоящая на втором месте справа и четвертом месте справа, означает, что во втором и четвертом разрядах единиц нет.)
Запиши с помощью цифр 9 и 0 одно пятизначное число и одно шестизначное число. Используя эти же цифры запиши другие многозначные числа.
6) на сравнение многозначных чисел:
Проверь, верны ли равенства: 5 312 < 5 320 900 001 > 901 000
Сравни числа:
а) 999... 1 000 б) 9 999... 999 в) 415 760... 415 670 г) 200 030... 200 003 д) 94 875... 94 895
При сравнении первой пары чисел ссылаются на порядок следования чисел в натуральном ряду: число последующее больше, чем число предыдущее.
При сравнении второй пары чисел ссылаются на количество знаков в записи чисел: трехзначное число всегда меньше, чем четырехзначное.
При сравнении третьей, четвертой и пятой пары чисел используют правило сравнения многозначных чисел: Чтобы узнать, какое из двух многозначных чисел больше, а какое меньше, поступают так:
Сравнивают числа поразрядно, начиная с высших разрядов.
Например, из двух чисел 34 567 и 43 567 больше второе, поскольку в разряде десятков тысяч оно содержит 4 единицы, а первое в том же разряде содержит три единицы.
Из двух чисел 415 760 и 415 670 больше первое, поскольку класс тысяч в обоих числах содержит одинаковое количество единиц — 415 ед. тыс., но в разряде сотен тысяч первое число содержит 7 единиц, а второе — 6 единиц.
Из двух чисел 200 030 и 200 003 больше первое, поскольку класс тысяч в обоих числах содержит одинаковое количество единиц — 200 ед. тыс., в разряде сотен оба числа содержат нули, в разряде десятков первое число содержит 3 единицы, а второе число в разряде десятков не имеет значащих цифр (содержит нуль), поэтому первое число больше.
Для большей наглядности при выполнении задания можно сравнивать две модели чисел из косточек на счетах (количественная модель).
Сравнивая многозначные числа, можно ссылаться на то, что число, содержащее в записи большее количество знаков всегда будет больше, чем число, содержащее меньшее количество знаков.
При сравнении чисел вида:
99 999... 100 000 567 999... 568 000 989 000... 989 001 599 999... 600 000
следует ссылаться на порядок следования чисел при счете: следующее число всегда больше, чем предыдущее.
7) на десятичный состав многозначных чисел:
Запиши числа: 376, 6 517, 85 742, 375 264. Сколько в каждом из них всего десятков? Подчеркни их.
Для определения количества десятков в многозначном числе можно прикрыть рукой последнюю цифру (первую справа). Оставшиеся цифры покажут количество десятков.
Для определения количества сотен в числе можно прикрыть рукой две последние цифры в записи числа (первую и вторую справа). Оставшиеся цифры покажут количество сотен в числе.
Например, в числе 2 846 — десятков 284, сотен — 28. В числе 375 264 - десятков 37 526, сотен - 3 752.
Рассмотри числа: 3849. 56018. 370843. Какое из подчеркнутых чисел показывает, сколько всего десятков в числе? Сотен? Тысяч?
Сколько всего сотен в числе 6 800?
Запиши 5 чисел, каждое из которых содержит 370 десятков.
8) на соотношения между разрядами:
Спиши, заполняя пропуски:
1 тыс. =...сот. 1 сот. =... дес. 1 тыс. =... дес.
Как изменятся числа 3 000, 8 000, 17 000, если отбросить l* их записи справа один нуль? Два нуля? Три нуля?
Сравни числа в каждом столбике. Во сколько раз увеличивается число, когда в его записи справа приписывают один нуль? Два нуля? Три нуля?
1 8 17
10 80 170
100 800 1 700
1 000 8 000 17 000
Числа 57, 90, 300 увеличь в 10 раз, в 1 ООО раз.
Числа 3 ООО, 60 000, 152 000 уменьши в 10 раз, в 100 раз, в 1 000 раз.
При выполнении последних двух заданий ссылаются на то, что увеличение числа в 10 раз переводит его в соседний разряд слева (десятки в сотни, сотни в тысячи и т.п.), а уменьшение числа в 10 раз переводит его в соседний разряд справа (десятки в единицы, сотни в десятки).
При увеличении числа в 10 раз (100,1 000) таким образом можно просто приписать справа нуль (два нуля, три нуля). При уменьшении числа в 10 раз (100, 1 000) можно отбросить справа один нуль в записи числа (два нуля, три нуля).
Завершает изучение класса тысяч знакомство с числом 1 000 000 (миллион).
Десять сотен тысяч — это миллион. Тысяча тысяч — это миллион. Миллион записывают так: 1 000 000. Число 1 000 000 завершает изучение чисел класса тысяч. Миллион (1 000 000) — это единица нового класса — класса миллионов.
Миллион (1 000 000) — первое семизначное число в ряду натуральных чисел.
Миллион — наименьшее семизначное число.
Миллион — новая счетная единица в десятичной системе счисления.
В записи числа 1 000 000 цифра 1 обозначает, что в VII разряде (разряде миллионов) — одна единица, а в разрядах сотен тысяч, десятков тысяч, единиц тысяч и т. д. нули означают, что в этих разрядах нет значащих цифр.
Класс миллионов содержит три разряда единицы миллионов, десятки миллионов и сотни миллионов (VII, VIII и IX разряды).
Завершает класс миллионов число миллиард.
Миллиард — это 1000 миллионов.
1000 миллиардов — это триллион.
1000 триллионов — это квадриллион.
1000 квадриллионов — это квинтиллион.
Представить себе такое количество чего-то невозможно. И.Я. Депман в «Истории арифметики» приводит такой пример для иллюстрации больших чисел: «Большегрузный железнодорожный вагон может вместить 50 миллионов рублей десятирублевыми билетами (купюрами). Для перевозки триллиона рублей понадобилось бы 20 тысяч вагонов».
Читают число так: 412 миллионов 163 тысячи 539 Записывают так: 412 163 539
Для чисел класса миллионов действуют правило чтения, правило записи и правило сравнения многозначных чисел (см. выше).
В стабильном учебнике математики для начальных классов числа свыше миллиона не рассматриваются.
Системы счисления
Десятичная система счисления
Системой счисления называют язык для наименования чисел, их записи и выполнения действий над ними.
Различают позиционные и непозиционные системы счисления. В позиционных системах один и тот же знак (цифра) может обозначать различные числа в зависимости от места (позиции), занимаемого этим знаком (цифрой) в записи числа.
Различные народы употребляли различные счетные группы. Большинство народов употребляло и употребляет десятичные группы счета или десятичную систему счисления. Единственной причиной выбора десятичной системы счисления является наличие у человека на руках десяти пальцев, которые служат удобнейшей вещественной основой для счета.
Для составления названий чисел по этой системе нужно иметь десять слов для названий первых десяти чисел и затем названия для новых счетных групп (сто, тысяча и т. д.). Добавление названий групп к числительным при счете позволяет обходиться десятью наименованиями числительных и десятью символами для записи чисел, соответствующих любому количеству.
В десятичной системе счисления для записи чисел используются 10 цифр (знаков, символов): 123456789 0. Из них образуют краткие записи чисел: 234, 56, 8 765 и т. п.
Каждая позиция в этой записи имеет свое название и свое условное значение: цифра, стоящая на первой позиции справа, означает количество единиц в числе; цифра, стоящая на второй позиции справа, означает количество десятков в числе и т. д. Таким образом, одна и та же цифра имеет различные значения в зависимости от места (позиции), где она записана. Благодаря этому свойству современную десятичную систему счисления называют позиционной. Десятичная позиционная система счисления позволяет записывать сколь угодно большие натуральные числа.
Позиционный способ записи чисел является очень удобным и экономичным, поскольку, позволяет обходиться десятью значками (цифрами) при записи всего бесконечного множества чисел. Однако сама структура системы является чисто условной, особенно для ребенка, которому мы не можем объяснить ни роль «основания» системы (десятка), ни схему увеличения степени основания при «движении» по позициям справа налево, т. е. запись вида:
234 = 2 • 102 + 3 • 101 + 4 • 10°
не может быть рассмотрена в начальной школе, поскольку ребенок не знаком с понятием степени и способом нахождения степени числа.
При знакомстве с десятичной системой счисления ребенок просто заучивает, что числа 10,100,1 000 и т.д. называют разрядными единицами первого, второго, третьего и т. д. разряда, и что при этом 10 единиц одного разряда составляют одну единицу следующего высшего разряда, т. е. отношение соседних разрядов равно 10 (фактически, отношения между разрядами — это просто степени числа 10).
В разные исторические периоды у некоторых народов имелись системы счисления с другими основаниями — 5,12, 20, 60. Например, древневавилонская система счисления была шестидесятиричная. Следы этой системы сохранились и сейчас в единицах измерения времени и величины угла: 1 час = 60 мин, 1 мин = 60 с, 1° - 60'.
Современные электронно-вычислительные машины используют двоичную систему счисления, основанную на обозначении чисел двумя цифрами 0 и 1. Например, число 2 (1 + 1) в ней будет записано как 10, а число 3 (2 + 1) — как 11.
В России десятичная система стала использоваться с XVII в. До этого времени числа записывались буквами славянского алфавита.
Римская система счисления
Примером непозиционной системы счисления без нуля может служить римская система. В ней числа от 1 до 20 обозначаются так:
I, II, III, IV, V, VI, VII, VIII, IX, X, XI, XII, XIII, XIV, XV, XVI, XVII, XVIII, XIX, XX.
Для записи больших чисел используют специальные обозначения: 50 - L, 100 - С, 500 - D, 1 000 - М.
Число 1917 в римской системе можно записать по-разному: МСМ XVII или MDCCCC XVII.
При этом первая запись предпочтительнее, поскольку четыре одинаковые цифры в записи числа римскими цифрами писать не принято.
В римской системе счисления используется принцип суммирования (его иногда называют принципом вычитания) при записи чисел: если меньшая цифра стоит после большей (справа), то она прибавляется к большей: MD = 1500, XVII = 17. Если меньшая цифра стоит перед большей (слева), то она вычитается: СМ = 900, IV = 4.
Римские цифры продолжали использовать в школьных учебниках и после проникновения в Европу современных цифр, поэтому их называли школьными.
Римскую запись чисел используют и сейчас для обозначения веков, глав книги, часов на круглых стрелочных циферблатах и т. п.,(поэтому во всех учебниках математики для начальных классов дети знакомятся с этой символикой.
Глава 3
|
|
|


