 |
Лекция 8. Вычислительные приемы сложения и вычитания для чисел первой сотни
|
|
|
|
1. Используемые математические законы и правила.
2. Способы устных вычислений.
3. Способы письменных вычислений (в столбик).
Используемые математические законы и правила
Правило группировки слагаемых
Правило группировки слагаемых играет роль вычислительного приема, позволяющего рационализировать вычислительную деятельность. Это правило может быть использовано при выполнении действий в выражениях, содержащих двух слагаемых. При этом обязательно следует отметить, что это правило касается только выражений, содержащих действие сложения. Правило изучается во 2 классе.
Правило группировки слагаемых:
При сложении трех и более чисел соседние слагаемые можно заменять их суммой.
Вычисли удобным способом:
3 + 6 + 4 =... 7 + 30 + 60 =...
90-70 + 5 =... 30 + 8 + 30 =...
(Легче сначала сложить 6 и 4 — это 10, затем прибавить к 10 число 3, получится 13.
Легче сначала сложить 30 и 60 — это 90, затем прибавить к сумме 7 — это 97.
Для случая 90 — 70 + 5правило группировки слагаемых неприменимо, поскольку это выражение содержит сложение и вычитание. В этом выражении действия надо выполнять по порядку слева направо.
Для случая 30 + 8 + 30легче сначала сложить 30 и 30 — это 60, а затем прибавить к сумме 8 — это 68.)
Правило сложения и вычитания разрядных единиц
Следствием правила группировки слагаемых выступают два следующих правила, определяющих способ сложения и вычитания разрядных единиц:
Единицы складывают с единицами. Десятки складывают с десятками.
Например, для случая 56+ 3 = 50 + (6 + 3) = 59
/\
50 6
удобно единицы складывать с единицами; для случая 60 + 35 = (60 + 30) + 5 = 95
/\
30 5
удобно десятки складывать с десятками.
В обоих случаях одно из слагаемых представлено в виде суммы разрядных слагаемых и выполняется прибавление чист к сумме разрядных слагаемых. В более ранних вариантах учебников математики для начальных классов правило прибавления числа к сумме и правило прибавления суммы к числу изучалось в явном виде (правило сообщалось детям и заучивалось как основа вычислительного приема).
|
|
|
Первое правило звучало так:
Чтобы прибавить число к сумме, можно прибавить его к любому слагаемому, а затем к полученной сумме прибавить оставшееся слагаемое.
Второе правило формулировалось так:
Чтобы прибавить сумму к числу, можно прибавлять к этому числу любое слагаемое суммы, а затем к полученному результату прибавить оставшееся слагаемое.
Правила были сочтены громоздкими и их заменили формулировками, сориентированными на поразрядное сложение. Однако для случаев вида 26 + 7 или 45+16 приходится использовать именно эти правила, а не правила поразрядного сложения.
Аналогичное упрощенное правило вводится для вычитания:
Десятки вычитают из десятков.
Единицы вычитают из единиц.
Например, для случая
29 - 3 = 20 + (9 - 3) = 26
/\
20 9
удобно единицы вычитать из единиц; для случая
56 - 30 = (50 - 30) + 6 – 26
/\
50 6
удобно десятки вычитать из десятков.
Однако для случаев вида 30 - 6,45 - 7,50 -24 эти правила приходится неявно заменять на общие правила вычитания числа из суммы и вычитания суммы из числа. Сами правила уже не рассматриваются в последней редакции учебника математики, но использовать их при вычислениях приходится. В связи с этим большая часть вычислительных приемов первой сотни предлагается детям в виде разбора образцов действий, а затем закрепления каждого способа действия на аналогичных примерах. С психологической точки зрения такой путь обучения вычислениям не ведет к становлению обобщенных приемов вычислительной деятельности.
Правило вычитания числа из суммы: чтобы вычесть число из суммы, можно вычесть это число из любого слагаемого, а затем к результату прибавить оставшееся слагаемое.
|
|
|
Например:
30-6 = 20 +(10-6) = 24
/\
20 + 10
В данном случае уменьшаемое 30 рассматривается как сумма 20 и 10.
Правило вычитания суммы из числа: чтобы вычесть сумму из числа, можно вычесть из этого числа любое слагаемое, а затем из полученного результата вычесть другое слагаемое.
Например: 45 - 7 = (45 - 5) - 2 = 40 - 2 = 38
/\
5 + 2
В данном случае вычитаемое 7 рассматривается как сумма 5 и 2.
Способы устных вычислений
При обучении устным вычислительным действиям ребенок осваивает в течение первого и второго года обучения в четырехлетней начальной школе целый ряд вычислительных приемов, из которых 12 относятся к вычислениям в пределах 100.
Вопрос о значимости формирования устных вычислительных навыков на сегодняшний день является весьма дискуссионным в методическом плане. Повсеместное использование калькуляторов ставит под сомнение необходимость «жесткой» отработки этих умений. На сегодняшний день никто не связывает хорошее владение арифметическими вычислениями с математическими способностями и математической одаренностью. Однако внимание к устным арифметическим вычислениям является традиционным для русской методической школы. В связи с этим более чем значительная часть всех существующих на сегодня учебников математики для начальных классов отведена формированию устных вычислительных умений и навыков.
Приведем традиционный порядок изучения вычислительных приемов в учебнике по математике авторов М.И. Моро, М.А. Байтовой, Г.В. Бельтюковой и др., поскольку данная система на сегодня является наиболее целостной и мелодически разработанной.
Основные типы вычислительных приемов, которые ребенок должен освоить для успешного формирования вычислительной деятельности в пределах 100:
1) 60 + 20; 50 - 30 — сложение и вычитание целыми десятками;
2) 34 + 20; 34 + 2 — прибавление единиц или десятков к числу без перехода через десяток;
3)26 + 4 — прибавление единиц к числу с получением в результате целого десятка, что приводит к увеличению разрядных единиц на одну в разряде десятков;
4) 48 - 30; 48 - 3 — вычитание единиц или десятков из числа без перехода через десяток;
5) 30 - 6 — вычитание единиц из целых десятков с заемом одного десятка;
|
|
|
6) 46 + 5 — прибавление единиц к числу с переходом через десяток;
7) 42 - 5 — вычитание единиц из числа с переходом через десяток;
8) 40 +16; 45 + 23 — сложение двузначных чисел без перехода через десяток;
9) 40 - 16 — вычитание двузначного числа из целых десятков с заемом десятков;
10) 45 - 12 — вычитание двузначных чисел без перехода через десяток;
11) 37 + 48 — сложение двузначных чисел с переходом через десяток;
12) 37 + 53 — сложение двузначных чисел с получением в результате целых десятков.
Методически все вычисления в пределах 100 считаются устными, что оговорено в учебном пособии для учителей начальных классов Байтовой М.А., Бельтюковой Г.В. «Методика преподавания математики в начальных классах»: «В методике различают устные и письменные приемы вычисления. К устным относятся все приемы для случаев вычислений в пределах 100, а также сводящиеся к ним приемы вычислений для случаев за пределами 100. К письменным относятся приемы для всех других случаев вычислений над числами, большими 100». (С. 163.)
На самом деле, уже при знакомстве со случаями вида 45 + 23 (прием 8), учитель знакомит детей со способами записи вычислительных действий «в столбик» и приемом поразрядного сложения, применяемым при письменных вычислениях.
Сначала предлагается устный способ вычислений:
45 + 23 =...
/\
20 3
(45 + 20) + 3 = 68
Затем отмечается, что удобно записать этот пример столбиком:
| + | ||
Далее приводятся подробные объяснения приема вычислений:
1. Пишу десятки под десятками, а единицы под единицами.
2. Складываю единицы: 5 + 3 = 8.
Пишу 8 под единицами.
3. Складываю десятки: 4 + 2 = 6.
Пишу 6 под десятками.
4. Читаю ответ: сумма равна 68.
Главным отличием письменных вычислений от устных является порядок складывания (или вычитания) разрядных единиц. При устных вычислениях всегда начинают со старших разрядов (в данном случае — с разряда десятков) и выполняют действие, двигаясь слева направо. При письменных вычислениях всегда начинают с разряда единиц и выполняют действие, двигаясь справа налево.
|
|
|
Методическое обоснование знакомства детей со способами письменных вычислений при формировании вычислительной деятельности в пределах 100:
1. Многие дети с большим трудом осваивают устные вычислительные действия с двузначными числами. Письменный прием вычислений облегчает им вычислительную деятельность.
2. Полноценное освоение устной вычислительной деятельности требует от ребенка свободного владения результатами табличных вычислений в пределах 10 и 20, свободного владения разрядным составом чисел, десятичным составом чисел, умением гибко и свободно применять разнообразные вычислительные действия, выбирая способ вычислений в каждом случае. Далеко не все дети могут это делать. Письменный способ вычислений требует более простых вычислительных действии, выполняемых по единому жесткому правилу (называемому «алгоритмом письменных вычислений»),
3. Знакомство со способами оформления вычислений «в столбик» при изучении вычислений в пределах 100 рассматривается как подготовка к использованию этой вычислительной технологии в дальнейшем (при вычислениях с трехзначными и многозначными числами).
Приведем краткие пояснения к технологии обучения ребенка вычислительным приемам в пределах 100.
Прием 60 + 20; 50-30- сложение и вычитание целыми десятками
Для освоения этого приема ребенок должен хорошо представлять десятичный состав двузначного числа. Рассматривая 60 как 6 десятков и 20 как 2 десятка, 60 + 20 вычисляется как 6 десятков + + 2 десятка. Ответ 8 десятков затем рассматривается как 80 и записывается результат вычислений. Таким образом, действия целыми десятками рассматриваются как действия разрядными единицами, вычисления в этом случае сводятся к табличным вычислениям в пределах 10.
Основные виды заданий, помогающих ребенку освоить данный прием:
1. Вычисли:
40 + 20 = 50-30 =
4 дес. + 2 дес. = 5 дес. — 3 дес. =
2. Вычисли:
6 дес. + 1 дес. = 6 дес. — 2 дес. =
5 дес. + 3 дес. = 1 дес. + 6 дес. =
4 дес. — 1 дес. = 8 дес. — 7 дес. =
3. Вычисли:
7+2= 6-3= 5-2=
70 + 20 = 60 - 30 = 50 - 20 =
4. Вставь числа в окошки, чтобы получились верные равенства:
4 + 2=□ 6-4 = □ □-10 = 30
40 + 20 = □ 60-40 = □ 80 — □= 10
50 + □ =90 □ + 60 = 70
5. Какое значение может принимать значок в каждой записи?
* + 3 = 8 6-... = 1
* -?... —?
# + 30 = 80 60 — @ = 10
#-? @-?
6. Сравни выражения:
60 - 20... 60 - 10 70 + 10... 10 + 70
60 + 20... 60 + 10 90 - 60... 70 - 60
7. Вычисли:
40 + 50 - 70 =... 50 - 40 + 90 =... 80 - 70 + 20 =...
Прием 34 + 20; 34 + 2 — прибавление единиц или десятков к числу без перехода через десяток
Схема приема:
34 + 20 = 54 34 + 2 = 36
/\ /\
30 4 30 4
50 6
Для освоения этого приема ребенок должен хорошо представлять себе разрядный состав двузначных чисел, уметь выполнять сложение целых десятков, сложение в пределах и разрядное сложение (50 + 4).
|
|
|
Виды заданий, помогающих ребенку освоить данный прием:
1. Найди ответ к данным примерам среди чисел, записанных ниже и покажи его стрелкой:
6 + 3 =... 5 + 7 =.. 6 + 2 =...
4 + 2 =... 3 + 4 =... 3 + 2 =...
7 8 6 9 5 12
2. Сравни выражения:
10 + 2... 10 + 20
56 + 30... 56 + 3
63 + 30... 63 + 3
47 + 20... 47 + 2
3. Выполни действия по образцу:
40 = 30 + 10 50 =... +...
70 = 60+ 10 30 =... +...
4. Найди значение каждой суммы, используя результаты первого примера:
34 + 2= 46 + 2= 72 + 2 =
34 + 3= 46 + 3= 72 + 3 =
34 + 4= 46 + 4= 72 + 4 =
5. Найди значение суммы, используя разрядный состав чисел:
46 + 20= 72+ 10 =
/\ /\
40 6 70 2
46 + 30 =... 72 + 20 =...
46 + 40 =... 72 + 30 =...
6. Найди значение суммы любым удобным тебе способом:
34 + 20=... 81 + 10=...
56 + 30 =... 45 + 30 =...
27 + 50 =... 63 + 20 =...
7. Вычисли значение выражений:
48-8 =... 80- 1 =... 30 + 8 =...
52-50 =... 79+ 1 =... 60- 1 =...
8. Вычисли значение выражений:
37-30 + 50 90- 1 -80 40 + 6 + 1
9. Догадайся, какие цифры нужно вставить в окошки, чтобы получились верные равенства.
34 + □= 64 17 + □= 97 46 + □= 96
52 + □=72 28 +□= 78 64 + □= 84
10. Вычисли результаты:
34 + 20= 28 + 30= 47 + 2 =
34 + 4 = 45 + 10 = 47 + 20 =
32 + 6= 15 + 4= 47 + 50 =
Прием 26 + 4 — прибавление единиц к числу с получением в результате целого десятка, что приводит к увеличению разрядных единиц на одну в разряде десятков
Схема приема: 24 + 6 - 30
/\
20 4

Для освоения данного приема ребенок должен знать разрядный состав чисел, уметь складывать в пределах 10 и выполнять прибавление десяти к целым десяткам.
Виды заданий, помогающих ребенку освоить данный прием:
1. Выбери из чисел справа верный ответ к примеру и обведи его:
6 + 4= (11,10,20)
8 + 2= (9,10,11)
7 + 3= (8,10)
4 + 6 = (9, 10, 8)
3 + 7= (7,10)
2. Вставь числа в окошки:
20 + 10 40 + □ □ + 10
30 60 90
3. Вычисли результаты, используя значение первого выражения в каждом столбике:
48 + 1 = 48 + 2 = 48 + 20 = 48 + 40 =
57 + 2 = 57 + 3 = 57+10 = 57 + 30 =
87-1 = 87-7 = 87-10 = 87 -70 =
16 + 4 = 26 + 4 = 36 + 4 = 46 + 4 =
4. Вставь число в окошко, чтобы равенство стало верным:
17 + □= 20 27 + □= 30 37 + 3 =□ 47 + 3= □
5. Какое значение может принимать буква в каждой записи:
73+ d=80 76 + z=80 # + 6 = 70
d-? z-? # -?
6. Найди ответы каждого примера среди чисел в кружках и соедини их стрелкой:
53 + 7 30 48 + 2 40 21 + 9 70
32 + 8 50 64 + 6 90 85 + 5 60
Прием 48- 30; 48- 3 — вычитание единиц или десятков из числа без перехода через десяток
 Схема приема: 48-3 = 45 48-30=18
Схема приема: 48-3 = 45 48-30=18
/\
40 8

Для освоения данного приема ребенок должен знать разрядные состав чисел, уметь вычитать в пределах 10 и выполнять разрядное сложение (40 + 5).
Виды заданий, помогающих ребенку освоить данный прием:
1. Среди чисел слева найди ответ примера справа и соедини их стрелкой:
3 8-3
5 7-5
2 9-6
6 8-4
4 9-3
2. Вставь числа в окошки, так чтобы равенства были верными:
18 — 3 = □ 10 — □ = 5
□ -3 = 7 19 — □ = 13
17 — □ = 12 □-6 = 4
3. Найди значение разности:
40 - 30 =... 50 - 20 =... 70 - 40 =...
4. Найди значение разности, используя разрядный состав чисел:
56-20= 36- 10 =
/\ /\
50 6 □ □
43-30 = 97 -80 =
/\ /\
□ □ □ □
50- 30 = 67 - 1 = 48-3=
96 - 20 = 67 - 2 = 48-4=
66 - 40 = 67 - 3 = 48-5=
67 -4= 48-6=
5. Сравнивай подчеркнутые цифры — это поможет тебе выполнить задание.
56-30...59-30
42+ 7...42+ 8
78-5... 78-7
26+ 30...25+ 30
6. Подчеркни удобный для тебя способ вычислений в каждом случае и вычисли:
а) (20 + 10) - 6 б) (40 + 10) - 2 в) (80 + 10) – 7
20+ (10-6) 40+ (10-2) 80+ (10-7)
(20-6)+ 10 (40-2)+ 10 (80-7)+ 10
7. Найди значение выражения в каждом случае, используя удобный для тебя способ:
39 - 7 = 56 + 4 = 80 + 1 =
68- 10= 56-4= 80- 1 =
19-5= 37 + 20= 34 + 5 =
73-20= 37 -20= 34-5 =
Прием 30-6 — вычитание единиц из целых десятков с заемом одного десятка
Схема приема: 30 - 6 - 24

Для освоения данного приема ребенок должен знать десятичный состав целых чисел, уметь вычитать в пределах 10 и выполнять разрядное сложение (20 + 4).
Виды заданий, помогающих ребенку освоить данный прием:
1. Заполни пустые окошки в равенствах по образцу:
30 = 20+ 10 40 = □ + □ 90 = □ + □
70 = 60+ 10 80 = □ + □ 100 = □ + □
2. Найди значения выражений в каждом столбике, используя первый ответ:
70 - 1 = 30 - 1 = 90 - 1 =
70-2= 30-2= 90-2 =
70-3= 30-3= 90-3 =
70-5= 30-6= 90-5 =
3. Вычисли, используя разложение целого числа, заданное схемой:
30 - 6 = 20 - 4 = 80 - 5 =
^ ^ ^
20 10 10 10 70 10
4. Найди парные примеры в соответствии со стрелками! и обозначь их такими же стрелками: |
70-8 24 + 6 90-7 36 + 4
30-6 62 + 8 40-4 83 + 7
50-9 55 + 5 40-6 34 + 6
60- 5 41 + 9 70-3 63 + 7
Можно ли считать парными по тому же принципу выражения 70 — 3 и 63 + 7? Исправь выражения так, чтобы они стали парными по тому же принципу.
5. Найди значения выражений удобным тебе способом:
53-40= 19-5= 76-30 =
28-7= 68- 10= 45-4 =
6. Какие значения могут принимать буквы в равенствах?
F+40 = 90 r+u=80
F—? u = 20
r—?
7. Вычисли, соблюдая порядок действий:
46-30-4= 23- 10 + 7 =
58 - 40 + 2 = 97 - 80 - 8 =
8. Найди ответы и соедини их стрелкой с примером:

70-6 58 50-5 13 20-7 45
9. Какое значение может принимать буква в равенстве?
50 - & = 4 28- L = 20 # + & = 70
& -? 30-L =.. 60 - # = 52
L-? &-?#-?
10. По какому правилу записаны ряды чисел? Продолжи каждый ряд:
| 12, | 22, | 32, | 42, | ... |
| 22, | 24, | 26, | 28, | 30, |
| 57, | 58, | 59, | 60, | |
| 86, | 85, | 84, | 83, | ... |
| 78, | 76, | 74, | 72, | 70, |
11. Найди и исправь ошибку:
50-6 = 36 30-7= 13
^ ^
40 10 □ □
70-3 = 63 40 - 2 = 38
^ ^
□ □ □ □
Прием 46 + 5 — прибавление единиц к числу с переходом через десяток
Схемы приема: 46+5=51 46+5=51
/ /\ /\ \
2 LnhtbEyPy07DMBBF90j8gzVIbCpqJ4Q0hEwqVIkNLIDSD3ASk0T4EWI3df+eYQXLmTm6c261jUaz Rc1+dBYhWQtgyrauG22PcPh4uimA+SBtJ7WzCuGsPGzry4tKlp072Xe17EPPKMT6UiIMIUwl574d lJF+7SZl6fbpZiMDjXPPu1meKNxongqRcyNHSx8GOandoNqv/dEgPL++rc5pzFffm7tmF5dCxxev Ea+v4uMDsKBi+IPhV5/UoSanxh1t55lGyBKREIqQ5tSJgCy7p0WDcFsI4HXF/zeofwAAAP//AwBQ SwECLQAUAAYACAAAACEAtoM4kv4AAADhAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlw ZXNdLnhtbFBLAQItABQABgAIAAAAIQA4/SH/1gAAAJQBAAALAAAAAAAAAAAAAAAAAC8BAABfcmVs cy8ucmVsc1BLAQItABQABgAIAAAAIQDMGR7s8QEAAOoDAAAOAAAAAAAAAAAAAAAAAC4CAABkcnMv ZTJvRG9jLnhtbFBLAQItABQABgAIAAAAIQDpYHtz3wAAAAkBAAAPAAAAAAAAAAAAAAAAAEsEAABk cnMvZG93bnJldi54bWxQSwUGAAAAAAQABADzAAAAVwUAAAAA " strokecolor="black [3040]"/>50 - 4 1 40 6 - 11
51 51
Для освоения данного приема ребенок должен знать состав однозначных чисел, уметь дополнять любое двузначное число до ближайшего целого, и выполнять разрядное сложение (50 + 1).
Виды заданий, помогающих ребенку освоить данный прием:
1. Какие числа нужно вставить в пустые окошки, чтобы сохранить закономерность?
10 7 3 …. 5 5 10 … 2
2. Вставь числа в окошки, чтобы равенства были верными:
7 + 5 =□ 5 + □=14 □+7 = 16 □+ 7 = 15
3. Найди ответы к примерам и соедини их стрелкой:
10 + 5 22 17 + 5 19 10 + 9 15
10 + 3 16 10 + 6 22 16 + 6 13
4. Назови и запиши сумму:

Прием 42-5 — вычитание единиц из числа с переходом через десяток
Схемы приема:
 42-5 = 37
42-5 = 37
/\
2 3

Для освоения данного приема ребенок должен знать состав однозначных чисел, уметь выделять десяток из любого двузначного числа, уметь вычитать в пределах 10 и выполнять разрядное сложение или сложение без перехода через десяток.
Виды заданий, помогающих ребенку освоить данный прием:
1. Вставь числа в окошки, чтобы равенства были верными:
7 + 5 = □ 4 + □ = 13 14 — □ = 6
12 — 5 = □ □ + 6 = 14 17 — □ = 8
□ + 7 = 15 □ -5 = 8
2.
3. Найди значение выражения:
35 - 5 = 67 - 7 = 98 - 8 =
54-4= 76-6= 43-3 =
4. Найди значение каждого выражения, используя первый ответ каждого столбика:
42-2= 54- 4 = 76-6 =
42-3= 54-5= 76-7 =
42-4= 54-6= 76-8 =
42 - 5 = 54 - 7 = 76 - 9 =
5. Найди ответы, используя схемы:
57-8 =

7 1
63-6 =

3 3

6. Дополни схемы и найди ответы:
43-5= 53-7 =


7. Найди значение выражений удобным тебе способом:
58-7= 78-9 =
65 - 6 = 34 - 6 =
8. Сравни выражения:
37 + 20....37 + 2
61 — 40...61-4
58 + 7... 55 + 7
83-9... 86-9
Прием 40 + 16; 45 + 23 — сложение двузначных чисел без перехода через десяток
Схема приема: 40 + 16 = 56
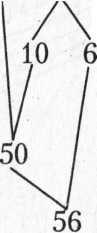
Для освоения данного приема ребенок должен знать разрядный состав двузначных чисел, уметь выполнять сложение разрядных единиц (десятки с десятками, единицы с единицами).
На основе этих же знаний и умений ребенок осваивает следующий прием.
Прием 45 - 12 — вычитание двузначных чисел без перехода через десяток
Схема приема: 45 - 12 = 33
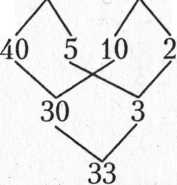
Виды заданий, помогающих ребенку освоить данный прием:
1. Найди ответ каждого примера в цепочке примеров и покажи стрелкой:
5 + 2
7-6
1+4
5 + 4
9-6
3 + 5
8-3
2. Вставь числа в окошки, чтобы равенства были верными:
40 + □ = 50 50 + □ = 90 □+40 = 60
70-□ = 60 □-30 = 60 90-□=40
3. Вычисли, используя схемы:
45 + 12 = 45 - 12 =
/\ /\
10 2 10 2
59-16 =
/\
10 6
21+24 =
/\
20 4
4. Найди значение выражений любым удобным тебе способом:
55+ 12= 55- 12= 53 + 35 =
31 + 24= 47-26= 54-33 =
45+ 14= 69- 16 =
Прием 40- 16 — вычитание двузначного числа из целых десятков с заемом десятков
Схема приема:

Прием является технически довольно сложным. Для его выполнения требуется выполнить ступенчатые «расщепления» числа 40, последовательно занимая десятки для вычитания сначала 10, затем 6.
Виды заданий, помогающих ребенку освоить данный прием:
1. Добавь нужные числа на крышах домиков.

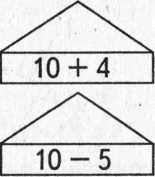

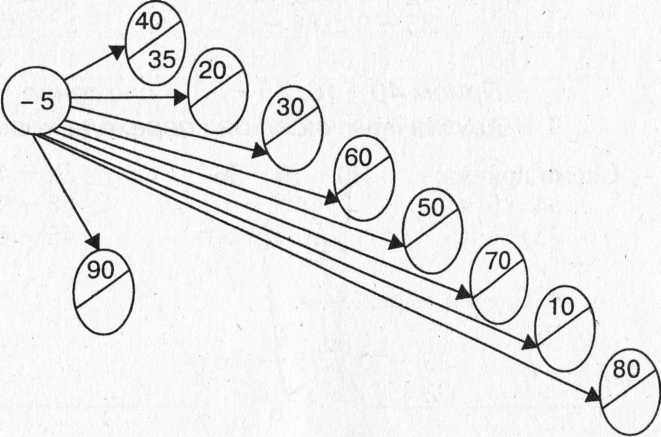
2. Найди ответы примеров и покажи стрелкой:

б) 40-6 42 70-5 36 50- 8 65
3. Напиши в кружках нужные числа:

4. Найди сумму, используя схему:
40+16 =
/\
10 6
60 + 38 =
/\
30 8
5. Выполни вычитание, используя схему:
40- 16= 70- 35 =
/\ /\
10 6 30 5
50-28= 90-47 =
/\ /\
20 8 40 7
6. Найди значение выражений любым удобным тебе способом:
50 + 26= 60+ 19= 90-37 =
/\
□ □
70 + 14 = 60 - 28 = 30 + 23 =
/\
□ □
7. Выбери знак, который можно поставить в окошко, и значение ответа из двух чисел в скобках:
70 □ 46 = (24, 34) 80 □ 17 = (53, 63)
20 □ 13 = (33, 48) 90 □ 19 = (81, 71)
Прием 37 + 48 — сложение двузначных чисел с переходом через десяток
При выполнении данного приема в уме (устно) каждое число раскладывается на разрядные составляющие, а затем разрядные единицы складываются: десятки с десятками, единицы с единицами. Получившиеся суммы снова складываются.
Для успешного выполнения этого приема ребенок должен хорошо знать разрядный состав двузначных чисел, уметь складывать целые десятки и складывать однозначные числа в пределах 20.
Прием 37 + 53 — сложение двузначных чисел с получением в результате целых десятков
Выполнение этого приема требует тех же знаний и умений, что и предыдущий прием. Способ выполнения тот же. При устном выполнении данный случай не вызывает затруднений, но при письменном выполнении ребенок может терять разрядную единицу, поскольку при письменном выполнении действия начинают выполнять с разряда единиц и вновь полученную разрядную единицу следует добавить дополнительно к сумме десятков.
Прием, облегчающий ребенку выполнение устных вычислений в пределах 100
Значительная часть детей испытывает большие трудности при устных вычислениях в пределах 100. Учить детей сразу приемам письменных вычислений — значит с первых же шагов обрекать их на полную беспомощность при выполнении устных вычислений уже в пределах 100. Научить приемам письменных вычислений иногда проще, чем пытаться развивать собственную вычислительную деятельность ребенка. Однако в практической жизни людям довольно часто приходится выполнять несложные (в пределах 100) вычисления в уме, а также довольно часто требуется умение оценить возможные границы результатов несложных вычислений. Психологами доказано, что формирование и развитие собственной вычислительной деятельности ребенка благотворно действует на развитие внутреннего плана действий, гибкости и рациональности мышления.
Особые трудности с устными вычислениями часто испытывают дети с замедленным типом мышления, дети с ведущим синтетическим способом мыслительной деятельности, а также ведущие кинестетики (дети, которые предпочитают опору на пальцевый счет).
Для детей с преобладанием синтетического типа мыслительной деятельности и для детей с замедленной мыслительной деятельностью были разработаны специальные схематические модели двузначных чисел, отражающие их десятичную структуру. На базе использования этих моделей (как основы для построения адекватной схематической модели приема) для этих детей была разработана иная последовательность знакомства с вычислительными приемами и иные способы их выполнения. Использование этих способов при устных вычислениях лишь в небольшой степени меняет порядок изучения вычислительных приемов приведенный выше.
Традиционно в начальной школе мы уделяем наибольшее внимание разрядной структуре двузначного и многозначных чисел, гораздо меньше внимания уделяется их десятичной структуре, хотя десяток является основанием десятичной системы счисления. Это можно объяснить тем, что познакомить ребенка с разрядным разложением числа мы можем уже в первом классе, используя понятие «разрядные слагаемые», т. е. 39 = 30 + 9, а чтобы познакомить
его с десятичным разложением того же числа пришлось бы использовать запись 39 = 10-3 + 9.
Поскольку знакомство с действием умножения по сегодняшним вариантам программ по математике для начальных классов предполагается лишь во втором классе, такая запись, естественно, в 1 классе не может быть использована.
Соответственно понятию «разрядный состав двузначного числа», мы рассматриваем два случая так называемого разрядного сложения и вычитания, которые в дальнейшем становятся одним из опорных приемов для обучения сложению и вычитанию с переходом через десяток и других вычислительных приемов в пределах 100. В соответствии с разрядным составом строится и схематическая разрядная модель числа, с которой связываются соответствующие случаи сложения и вычитания:
39 30 + 9 39-9
/\
30 9 9 + 30 39-30
Для детей с трудностями вычислительной деятельности предлагается другая схематическая модель двузначного числа, имеющая в основе его десятичный состав. Использование схематической десятичной модели, доступной восприятию первоклассника, позволило обойти невозможность использования аналитической записи, отражающей десятичную структуру числа.
С другой стороны, данная модель позволяет эффективно использовать мыслительные особенности ребенка с преобладанием синтетического типа мышления (а их среди первоклассников большинство), которые предрасположены к работе с наглядными моделями изучаемых понятий. Используемая модель понятия (двузначного числа) позволяет такому ребенку в конкретной деятельности моделировать сам прием вычисления, в то же время являясь основой для самопроверки (т. е. дает возможность убедиться в правильности ответа). Десятичная модель числа выглядит следующим образом (дети назвали ее «солнышко»):
10  9
9
10 10
С этой моделью связаны следующие случаи сложения и вычитания:
39-9 39- 10 39-20 30 + 9
39- 19 39-29 39-30 9 + 30
Как видим, их гораздо больше, чем в случае опоры на разрядную модель. В то же время, все эти случаи не выходят за рамки десятичного состава числа 39, воплощенного в его схематической модели.
Используя эту модель, ребенок не только осваивает вышеозначенные случаи вычисления, представляя себе суть приема на наглядном уровне, но и действуя руками (просто закрывая на модели пальцем или ладонью вычитаемое), сразу же проверяет правильность полученного ответа:
10  9
9
10 10
39 - 19 - 20
Таким образом, формируется прием собственной вычислительной деятельности ребенка.
Поскольку для чисел второго десятка десятичная модель совпадает с разрядной, использование этого приема моделирования при знакомстве с разрядным сложением и вычитанием в пределах 20, наряду с рассматриваемыми там предметными моделями (кубиками, палочками) будет носить ознакомительный характер:
/\
10 9
10 + 9 9+10
19-10 19-9
Активное использование этих моделей для осознания десятичной структуры двузначного числа при изучении нумерации двузначных чисел позволит создать прочную базу для усвоения вычислительных приемов в пределах 100.
Приведем варианты вычислений, которые позволяет организовать использование десятичной модели двузначного числа:
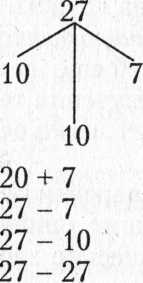

27-10-10 27-20 27-10-7 27-17
34-10 34-20 34 - 30 30 + 4
34-4 34-14 34-24 34 + 2

| 10 10 | ||||
| -5 | -30 | 65 + 1 | ||
| - 10 | -35 | 65-1 | ||
| -20 | -45 | 65 + 2 | ||
| -50 | -55 | 65-2 | ||
| -40 | -25 | 65 + 3 | ||
| -15 - | 65-3 |
65-5 65 + 5
Детям, которым трудно даются арифметические вычисления, такая модель значительно облегчает работу. Используя эту модель, для этих детей можно разработать индивидуальный путь освоения и других случаев вычислений, например:
42 + 3 = 45


10 10 10
На первый взгляд, такая схема приема производит гораздо более громоздкое впечатление, чем его аналитическая запись:
45 + 7 = 45 + (5 + 2) - (45 + 5) + 2 = 50 + 2 = 52
Однако в отношении тех детей, о которых идет речь (синтетики с замедленным типом мышления, необходимо требующие наглядной внешней опоры для формирования осознанного типа деятельности), такая модель оказывается более эффективной в связи со своей наглядностью, а чуть большая затрата труда и времени для построения этой модели (самостоятельного рисования десятичной схемы числа) этих детей не отвращает, наоборот, она служит как бы приемом подготовительно-организующим дальнейшую вычислительную деятельность. Использование таких моделей еще на этапе изучения нумерации в пределах 100 (до начала изучения темы «Сложение и вычитание в пределах 100»), позволяет легко освоить первые девять приемов вычислений.
Использовать ли десятичную схему и дальше или перейти к аналитической записи приема вычисления, учитель решит, ориентируясь на преобладающие индивидуально-типологические характеристики учеников своего класса.
|
|
|


