 |
Постановка задачи
|
|
|
|
Исследование квантовых свойств СИ оказалось весьма интересным с точки зрения развития
квантовой теории макроскопического движения и привело к открытию принципиальных, порою неожиданных эффектов, имеющих фундаментальное теоретическое и практическое значение.
Первоначальные соображения о возможности проявления квантовых эффектов в СИ были неочевидными: СИ в своих главных чертах хорошо описывались методами классической электродинамики Максвелла- Лоренца, и основные выводы этой теории с большой степенью надежности были подтверждены экспериментально. Так что необходимость исследования квантовых закономерностей СИ – дискретных свойств макроскопического явления – представлялась спорной.
Действительно, обычный критерий применимости классических методов описания излучения релятивистского заряда заключается в том, что энергия испускаемого фотона Eф должна быть мала по сравнению с энергией электрона
E. При этом, как указали В. В. Владимирский и Швингер, квантовые эффекты могут проявляться только в том случае, если эти величины станут соизмеримы:
Eф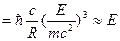 
Таким образом, условием возможности классического описания СИ был критерий:
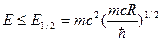
Этот критерий подтверждался также соображениями инвариантности, в силу чего мощность синхротронного излучения, будучи инвариантной, должна зависеть только от инвариантных параметров, одним из которых является:
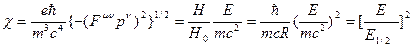
Где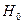 
= 
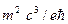= 4, 41* 
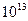Гс -- швингеровское значение магнитного поля; 
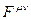-- тензор электромагнитного поля; 
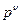-- четырехмерный вектор – импульс электрона. Оценка энергии, определяемой критерием 
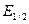, для реальных параметров ускорителей приводит к значению 
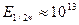эВ, чтоб далеко превосходит энергию частиц не только в действующих, но также и в планируемых на обозримое будущее ускорителях.
|
|
|
Вместе с тем оказалось, что критерий 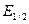не вскрывает всех особенностей, связанных с дискретными свойствами СИ, и прежде всего это касается проблемы влияния дискретности излучения на движение частицы. Действительно, поскольку энергия излучаемого фотона в максимуме спектра СИ достаточно велика Eф 
,
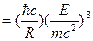число таких фотонов, излучаемых за время одного оборота электрона, конечно и равно:
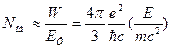
Для более наглядной оценки фактора дискретности излучения можно найти длину пути (в сантиметрах ), проходимого электроном без испускания высокоэнергетических фотонов,
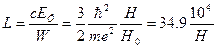
Как видно, это выражение зависит только от напряженности магнитного поля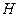 
, и при обычных значениях (для ускорителей и накопительных колец) порядка 
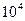Гс следует, что в среднем один высокоэнергетический фотон излучается на пути 30 см.
Дискретность излучения, выступающая здесь как важный фактор, может сказаться на траектории частицы, вызывая её квантовые флуктуации как следствие эффекта отдачи, испытываемой электроном при испускании им фотонов.
Для определения критерия возбуждения квантовых флуктуаций траектории электрона рассмотрим выражение для его энергетического спектра в постоянном однородном магнитном поле, направленном по оси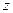 
, а также:
Здесь орбитальное квантовое число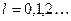 
соответствует квантованию вращательного движения частицы, а 
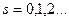-- радиальное число, имеющее связь с флуктуацией радиуса орбиты вращения:
.
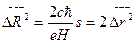Возбуждение квантовых флуктуаций траектории влечет за собой флуктуации энергии частицы
|
|
|
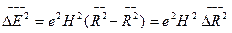
Поэтому критерий возникновения таких флуктуаций можно установить исходя из условия
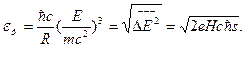
Для критического значения энергии, при котором становится возможным возбуждение радиальных степеней свободы (появление числа 
), следует (при 
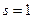), что
.
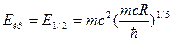Это соответствует энергии электрона 500-1000 МэВ, т. е. области энергий действующих ускорителей и накопительных колец. Критерий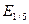 
как условие возбуждения радиальных степеней свободы электрона был впервые указан А. А. Соколовым в 1949 г., который положил начало развитию квантовой теории синхротронного излучения.
Таким образом, критическое значение энергии электрона (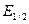 
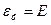) устанавливает пределы применимости классической теории излучения, а ( 
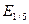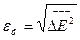) соответствует проявлению квантовых эффектов, связанных с влиянием дискретности СИ на траекторию движения частицы. Критерий 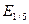выделяет по существу «квазиквантовую» область энергий: классическое описание излучения уже еще остается справедливым, однако дискретный характер излучения уже начинает проявляться в виде квантовых флуктуаций траектории электрона.
Последовательное развитие квантовой теории СИ подтвердило оба критерия ( 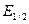и 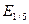) и дало возможность выявить физическое содержание квантовых закономерностей в условиях макроскопического движения.
С одной стороны, строгими методами квантовой теории было установлено, в частности, что квантовые поправки к классическому выражению для мощности синхротронного излучения имеют характер разложения по параметру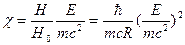 
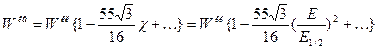
в предположении его малости, т. е. при условии 
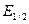« . При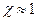 
классическая теория изучения становиться полностью неприменимой.
С другой стороны, более детальный анализ квантовых свойств синхротронного излучения показал, что начиная с энергий 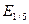возникает особое квантовое явление (не свойственное классической теории): флуктуации радиуса орбиты электрона – квантовое уширение траектории. При этом электрон движется подобно Броуновской частице, испытывая стохастические воздействия при испускании фотонов.
Большой интерес развитие квантовой теории СИ представляло в связи с задачей изучения поведения спина электрона в условиях высоких энергий частиц.
|
|
|
Развитие квантовой теории СИ с учетом спиновых свойств электрона привело к открытию эффекта радиационной поляризации электронов и позитронов в накопительных кольцах. Вследствие этого эффекта неполяризованный вначале пучок электронов по причине синхротронного излучения приобретает преимущественную ориентацию спина против направления магнитного поля. Ориентация спинов позитронов оказывается противоположной.
Развитие квантовой теории макроскопического движения открывает также возможность исследования состояний электрона в магнитном поле в экстремальных условия, когда напряженность поля 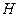достигает очень больших значений – порядка швингеровского поля 
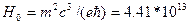Гс. Это представляет особый интерес в решении ряда задач астрофизики в связи с тем, что подобные магнитные поля существуют вблизи нейтронных звезд – пульсаров. Изучение поведения вещества в этих условиях возможно только методами квантовой теории.
Приведенные здесь соображения легли в основу построения квантовой теории движения и излучения электронов в магнитном поле.
Развитие квантовой теории СИ целесообразно проводить на основе квантовой релятивистской механики и квантовой электродинамики, применяя так называемый метод точных решений уравнения Дирака. В соответствии с этим методом волновая функция, описывающая квантовые состояния электрона, подчинена уравнению Дирака
,
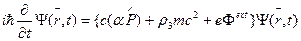где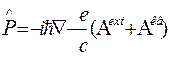 
-- кинетический импульс; 
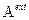и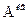 
относятся соответственно к внешнему электромагнитному полю( 
, 
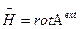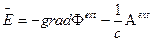) и квантовому поперечному полю излучения 
( 
).
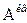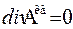Обычная теория возмущений, предполагающая путь решения уравнения Дирака в виде разложения волновой функции в ряд по внешнему полю ( ,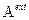 
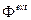), здесь не применима, так как эффекты, связанные с внешним полем (в особенности в случае сильного поля), могут быть существенно нелинейными. Вместе с тем процессы, происходящие с электроном в связанном состоянии при его взаимодействии с электромагнитным полем излучения (константа взаимодействия 
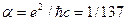), можно при этом рассматривать по теории возмущений, имея в виду точное определение волновой функции «нулевого» приближения в связанном состоянии. Таким образом, в уравнении Дирака внешнее электромагнитное поле 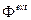, 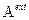учитывает точно, а квантованное поле излучения 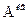-- по теории возмущений.
|
|
|
При таком подходе все разложения в теории возмущений производят по полной системе волновых функций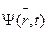 
, являющихся точными решениями уравнения Дирака для электрона в связанном состоянии. Впервые в задаче о синхротронном излучении этот метод был предложен А. А. Соколовым. Позже метод точных решений получил название картины Фарри, который показал, что формализм Фейнмана – Дайсона можно обобщить на случай, когда электрон не свободен, а находится в связанном состоянии.
Метод точных решений дает возможность учесть любые значения напряженности внешнего поля. В частности, в случае магнитного поля в силу устойчивости вакуума допустимо рассматривать даже значения напряженности поля большие критического значения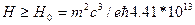 
Гс, существующие, по-видимому, в глубине пульсаров.
В магнитном поле сколь угодно большой напряженности рождение электрон-позитронных пар из вакуума не происходит и метод точных решений не имеет огрничений, связанных с напряженностью магнитного поля .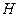
|
|
|
