 |
Взаимодействие электрона с полем излучения.
|
|
|
|
Квантовые закономерности в интенсивности СИ.
Согласно квантовой теории будем рассматривать излучение электромагнитных волн движущимся электроном как результат спонтанных переходов электрона в более низкое энергетическое состояние. Как известно, физической причиной таких переходов является взаимодействие электрона с полем излучения: это взаимодействие электрона с полем излучения: это взаимодействие не прекращается даже тогда, когда в начальный момент времени реальные фотоны отсутствуют (взаимодействие с электромагнитным вакуумом). Наиболее последовательной постановкой задачи об излучении является рассмотрение взаимодействия электронов с квантованным полем излучения в предположении, что сами электроны описываются волновыми функциями — решениями уравнения Дирака, учитывающими внешнее магнитное поле точно. Такой метод решения задачи (метод точных решений), в основе которого лежит описание частицы с помощью волновой функции, точно учитывающей внешнее электромагнитное поле, дал возможность не только теоретически предсказать ряд важных закономерностей в синхротронном излучении, но и получить их точное описание.
Как известно, волновая функция поперечного электромагнитного поля излучения в вакууме может быть представлена в виде фурье-разложения векторного потенциала по плоским волнам
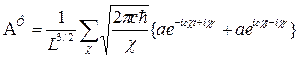
Поскольку электромагнитное поле поперечно, удобно взять калибровку потенциала в виде 
, т. е. 
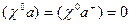, где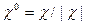 
. Для квантованного поля фотонов амплитуды 
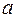и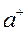 
являются операторами рождения и уничтожения частиц и подчиняются перестановочным соотношением для бозе-поля:
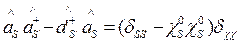
где индексы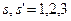 
соответствуют проекции амплитуд вектор-потенциала на оси координат. При исследовании спонтанного излучения, когда в начальный момент времени фотоны отсутствуют, отличными от нуля остаются лишь следующие билинейные комбинации
|
|
|
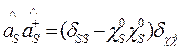
автоматически учитывающие рождение фотонов.
Поляризационные свойства излучения можно рассмотреть методом, аналогичным классической теории. В целях исследования линейной поляризации разобьем амплитуду поля фотонов а на две взаимно перпендикулярные составляющие
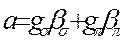
где единичные векторы 
соответствуют 
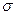- и 
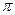-компонентам линейной поляризации:
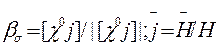
Вектор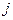 
направлен вдоль магнитного поля. Для рассмотрения круговой поляризации следует представить амплитуду 
в виде
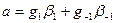
где
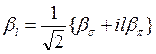
причем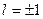 
соответствует двум состояниям круговой поляризации (правой 
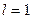и левой 
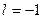). Перестановочные соотношения для амплитуд 
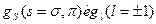имеют особо простой вид
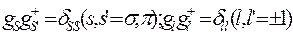
Введем далее взаимодействие электрона с полем фотонов в гамильтониан уравнения Дирака
При этом энергия взаимодействия, рассматриваемая далее по теории возмущений,
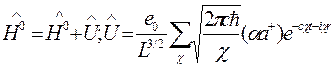
Дальнейшее рассмотрение проводится обычным методом теории возмущений в виде необходимых разложений матричных элементов по функциям нулевого приближения — точным решениям уравнения Дирака для электрона во внешнем поле (представление Фарри).
В результате достаточно стандартного расчета можно получить выражения для вероятности квантовых переходов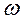 
и мощности синхротронного излучения W:
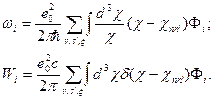(16)
Эти выражения соответствуют квантовому переходу электрона из состояния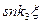 
, и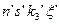 
индекс i соответствует компонентам поляризации излучения, 
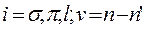. Функция 
, -, учитывающая поляризационные свойства излучения, связана с элементами матриц Дирака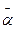 
:
;
;
,
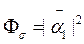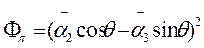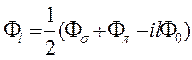где
( 
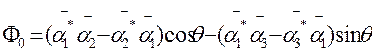
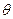— угол между направлениями поля Н(ось 
) 
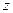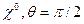соответствует плоскости орбиты вращения электрона). Матричные элементы матриц Дирака
|
|
|
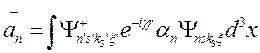
выражаются через функции Лагерра Inn’(x) и /SS'(x), где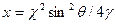 
. При этом
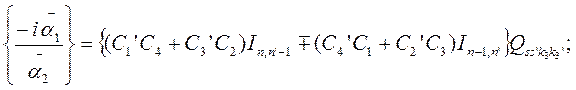
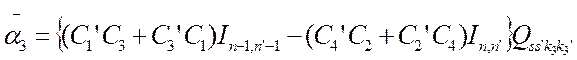
(17)
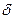-функция в правой части (17) выражает закон сохранения импульса вдоль поля — учитывает эффект отдачи при излучении электроном фотона, спиновые коэффициенты 
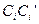зависят от ориентации спина в начальном 
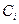, и конечном 
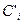состояниях, 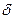-функция связана с законом сохранения энергии при излучении фотона.
Приведенные здесь общие формулы, входящие в выражение для мощности излучения (16), открывают возможность исследования всех характеристик синхротронного излучения для любых значений энергии частицы (включая и низшие уровни) и напряженности магнитного поля. Сейчас, однако, рассмотрим случай движения электрона по макроскопической орбите, когда значения квантовых чисел 
и 
очень велики. Это дает возможность, в частности, перейти к непрерывному спектру, заменив суммирование в (16) интегрированием по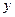 
:
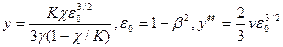
где
при этом
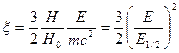
связана с инвариантом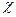 
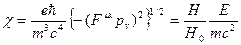(18)
Здесь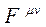 
— тензор электромагнитного поля. В случае квазиклассического движения, когда квантовые числа принимают очень большие значения, функции Лагерра 
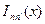могут быть аппроксимированы функциями Бесселя постоянного индекса 1/3 — функциями Макдональда
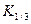
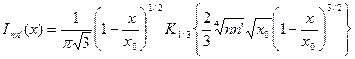
причем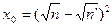 
. Эту аппроксимацию можно положить в основу выражения для мощности синхротронного излучения. Следуя правилам, получаем
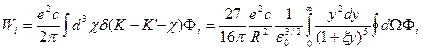(19)
где , характеризующие компоненты линейной поляризации СИ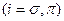 
, имеют вид
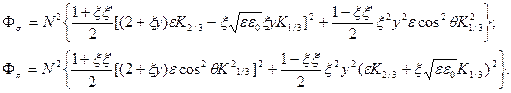(20)
При этом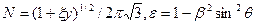 
— функции 
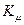— зависят от аргумента 
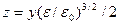. Эти формулы полностью характеризуют спектрально-угловое распределение мощности синхротронного излучения, включая квантовые переходы электрона с изменением ориентации спина (так называемые spin-flip-переходы). Мы не рассматриваем круговую поляризацию излучения и не приводим детальных расчетов.
Далее прежде всего остановимся на выражении для спектрального распределения мощности СИ и с этой целью проинтегрируем (19), (20) по телесному углу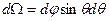 
. Эти интегралы можно взять точно, и тогда можно получить
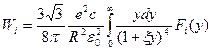(21)
где
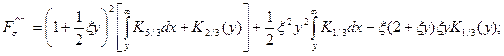
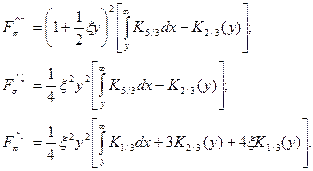(22)
Как видно из (22), мощность синхротронного излучения зависит только от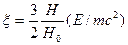 
. Действительно, поскольку мощность излучения является инвариантной, зависимость от параметра 
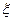, имеющего прямую связь с инвариантом (18), является вполне очевидной. Представляет интерес оценить значение 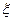для разной напряженности магнитного поля, включая экстремальные поля, встречающиеся в природе. Так, в частности, для магнитных полей, применяемых обычно для ускорителей и накопительных колец, поле 
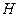имеет порядок 104 Гс, и тогда 
. Это очень маленькое значение, поэтому по параметру 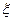возможно разложение всех выражений характеризующих мощность излучения. Это соответствует квантовым поправкам к классическому выражению для мощности СИ, поскольку параметр 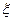содержит постоянную Планка 
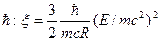. Для магнитного поля, наблюдавшегося вблизи белых карликов 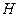~5-108 Гс, параметр 
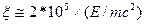остается малым вплоть до энергий электрона ~100ГэВ, а для магнитного поля, наблюдавшегося вблизи и поверхности пульсаров ~1012 Гс, параметр 
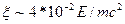, поэтому разложение по этому параметру имеет ограниченный предел по энергии электрона. В случае, если 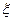порядка единицы и даже превышает это значение, разложение в виде ряда по параметру, содержащему постоянную Планка 
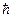, становится невозможным, и квантовые закономерности приобретают фундаментальное значение (ультраквантовый случай)
|
|
|
Формулы для мощности синхротронного излучения (21), (22) включают в себя также члены, соответствующие излучению, которое сопровождается переворотом спина (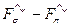 
компоненты). Как видно из этих выражений, мощность такого излучения пропорциональна квадрату 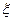, т. е. квадрату постоянной Планка 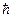. Поскольку 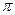- компонента излучения содержит явную зависимость от ориентации спина, синхротронное излучение, сопровождающееся переворотом спина, оказывает влияние на его ориентацию и стимулирует направленный процесс поляризации пучка электронов.
Обращает на себя внимание, что зависимость от ориентации спина входит также в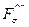 
- компоненту излучения, не сопровождающегося изменением поляризации.
Важно, что это имеет не только академический интерес. Действительно, в предположении малости параметра 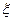(квазиквантовый случай 
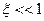) можно ограничиться в (22) линейными по 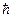членами, и тогда получим
|
|
|
`
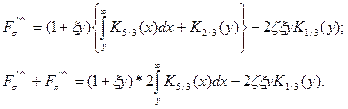Отсюда следует, что поляризованный пучок электронов со спином, ориентированным против магнитного поля ( 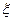< 0), будет излучать несколько больше, чем неполяризованный пучок. В коротковолновой области спектра ( 
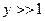) открывается наиболее благоприятная возможность для наблюдения спиновой зависимости СИ. При этом добавочная мощность СИ, связанная с ориентацией спина, имеет вид
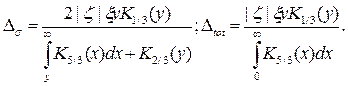
Тогда при 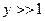, используя асимптотическое поведение функции Макдональда 
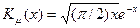, нетрудно получить, что
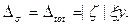
Поэтому при наблюдении мощности СИ на фиксированной частоте спектра можно определить поляризационные характеристики пучка частиц.
Найдем теперь выражение для мощности СИ, просуммированное по состояниям поляризации электрона и поляризации фотонов:
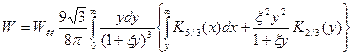
и сравним это с формулой мощности синхротронного излучения, испускаемого бесспиновой частицей (бозоном со спином 0 ),
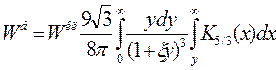
Разность этих выражений, обязанная излучению частицей со спином 1/2, равна
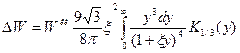
и при малых 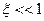это выражение дает
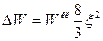
Мы вернемся к обсуждению физического содержания этой величины, пока лишь отметим, что разность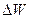 
в этих формулах соответствует мощности излучения неполяризованного электрона и ее значение пропорционально квадрату постоянной Планка 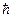. Для поляризованного электрона (имеющего ориентированный спин) различие в мощности излучения по сравнению с бесспинвой частицей проявляется уже в членах, линейных по .
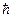Рассмотрим теперь интегральную мощность СИ и с этой целью проинтегрируем выражение для матричных элементов (22) по спектру, т. е. по dy. Как видно из (21) и (22), вычисления сводятся к линейной комбинации интегралов типа
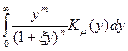
Впервые задача точного вычисления мощности СИ, равномерно пригодного для любых значений параметра 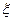, включая и ультраквантовую область, была решена В. Г. Багровым. При этом оказалось возможным выразить мощность излучения через специальные функции 
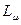,, связанные с функциями Бесселя 
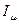от мнимого аргумента и функции Ангера:
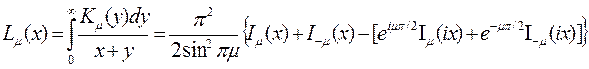
Таблицы значений этих функций дают возможность найти мощность СИ при любых заданных 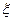. Мы, однако, рассмотрим асимптотические приближенные выражения, которые можно получить непосредственно из (21) и (22), минуя точное интегрирование. Прежде всего остановимся на случае, когда инвариантный параметр 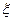меньше единицы. Физически это соответствует Критерию малости энергии излучаемых фотонов 
по сравнению с энергией электрона, т. е. случаю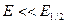 
(квазиквантовое приближение). Тогда, разлагая все величины, входящие в интегралы (21), по параметру 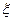и сохраняя члены не выше второго порядка малости 
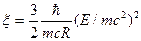, т. е. до второго порядка разложения по постоянной Планка 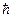, после интегрирования с помощью известного значения интеграла
|
|
|
(23)
[ 
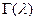—гамма-функция Эйлера] получаем
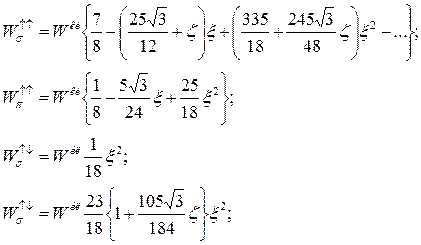(24)
Эти формулы наиболее полно описывают основные особенности квантовых поправок к классическому выражению для мощности синхротронного излучения WKJI. Из (23) видно, что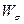 
- компонента излучения в случае поляризованного электрона зависит от начальной ориентации спина, причем эта зависимость входит в члены, пропорциональные первой степени постоянной Планка 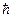. Переворот спина сказывается в членах, пропорциональных 
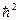, причем вероятность переворота в 
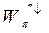- компоненте зависит от начальной ориентации спина, вследствие чего пучок электронов может получить преимущественную ориентацию спина. На этом мы остановимся более подробно позже при рассмотрении эффекта радиационной поляризации электронов и позитронов.
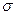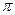Найдем теперь полное выражение для мощности синхротронного излучения, суммируя (24) по поляризациям: - и -компонентам, а также конечному спину, сохраняя начальную ориентацию спина 
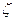. Тогда можно получить
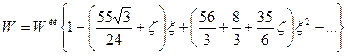
Несмотря на то что эти поправки были известны уже давно, интерес к их происхождению не исчезал, но до последнего времени физическая интерпретация встречала трудности. Эти трудности объясняются тем, что в релятивистской квантовой механике спиновые и орбитальные свойства частиц находятся в тесном единстве, и их раздельное истолкование, как это известно, возможно только в нерелятивистском приближении.
Введение ковариантных операторов поляризации, коммутирующих с гамильтонианом, и разделение с их помощью решений уравнения Дирака по спиновым состояниям можно рассматривать в этом отношении как известный шаг вперед, открывающий возможность исследования спиновых свойств релятивистских частиц наряду с орбитальным движением.
Существенный прогресс в квазиклассическом методе рассмотрения мощности СИ с учетом спиновых свойств электрона был достигнут В. А. Бородовицыным, которому удалось дать простое физическое объяснение всем квантовым поправкам к мощности синхротронного излучения, включая члены порядка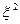 
, пропорциональные 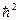. При этом движение электрона предполагается ультрарелятивистским, что исключает известный подход к интерпретации квантовых закономерностей путем разложения по параметрам, содержащим отношение 
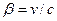. Приведем здесь краткие результаты этого анализа.
Поправка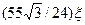 
, подтвержденная Швингером, характеризует вклад в излучение, обусловленный эффектом отдачи, испытываемой электроном при излучении фотона. Эффект отдачи одинаков для фермионов и бозонов, поэтому та же поправка входит и в мощность излучения бесспиновой частицы.
Более сложную природу имеет поправка пропорциональная 
, зависящая от ориентации спина электрона. Она свойственна только поляризационному электрону и при усреднении по спину (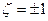 
) исчезает. Эта поправка, наиболее трудно поддающаяся объяснению, возникает из-за смешанного излучения электрона—заряда, движущегося по орбите и электрона — магнитного диполя. Таким образом, поправка отражает своеобразную связь спинового и орбитального движения частицы. Как было показано, при этом также проявляется эффективная масса частицы со спином во внешнем поле. Важно заметить, что поправка к мощности синхротронного излучения хотя и не связана с переворотом спина электрона, но тем не менее она оказывает влияние на его динамику. К этому вопросу мы вернемся несколько позже.
Рассмотрим члены в выражении для мощности СИ, пропорциональные 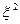(квадрату постоянной Планка), и постараемся им также дать физическое объяснение. Поправка 
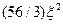, одинаковая для электронов и бесспиновой частицы, характеризует эффект отдачи при излучении во внешних членах по 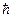, а поправка 
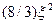является разностью 
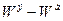и включает в себя наряду с эффектом отдачи также и переворот спина, т. е. излучение магнитного момента неполяризованного электрона. И, наконец, поправка 
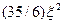содержит в совокупности вклад от интерференции излучения заряда и магнитного момента электрона, а также эффект отдачи, испытываемой поляризованным электроном.
Мы подробно остановились на вопросах интерпретации квантовых поправок к классическому выражению для мощности, поскольку это представляет интерес с точки зрения физического понимания квантовых закономерностей синхротронного излучения.
И в заключение изложения вопросов, связанных с квантовыми свойствами мощности СИ, рассмотрим ультраквантовый случай движения частицы, когда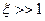 
. Такой случай может реализоваться в условиях экстремально сильных магнитных полей и высоких энергий частицы.
Возвращаясь к выражениям для мощности СИ, включающим любые значения параметров 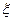, можно заметить, что множитель 
в знаменателе интеграла по спектру автоматически обрывает интеграл при 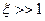, если переменная интегрирования 
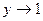, т. е. главный вклад дают значения 
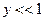- При этом для функций 
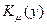можно воспользоваться асимптотическим выражением
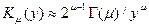
и тогда, имея в виду значение интеграла
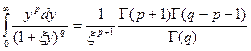
можно получить
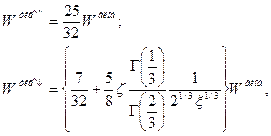(25)
где 
— глобальная (полная) мощность излучения, в отличие от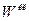 
она имеет вид
(26)
Из полученных формул следует, что при больших значениях энергии электрона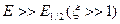 
переходы с изменением ориентации спина вносят вклад в основной член полной мощности. При этом уменьшается направленность в изменении ориентации спина, поскольку, как это видно из (25), мощность СИ слабо зависит от начальной ориентации спина.
Важно заметить, что в отличие от квазиклассического случая Движения частицы, когда 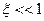и квантовые эффекты дают малые поправки к классическим формулам, в ультраквантовом случае основной член является квантовым и переход к классическому приближению невозможен.
В квазиклассическом случае движения электрона максимум излучения соответствует частоте
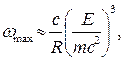
ав ультраквантовом случае спектр обрывается на частоте
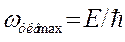(27)
намного меньшей, чем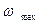 
Действительно, электрон не может излучать энергию больше, чем его энергия Е. Это наглядно следует из общего выражения для частоты излучения
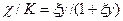или 
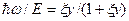(28)
При 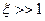отсюда следует сразу же (27). Заметим также, что из этой формулы в квазиклассическом случае, когда 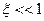, получается и обычное значение критической частоты (28), если иметь в виду, что переменная интегрирования порядка единицы: 
.
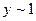Соответствующие вычисления глобальной мощности синхро-тронного излучения, проведенные для бесспиновой частицы, приводят к значению (26), но с численным коэффициентом почти в 2 раза меньше: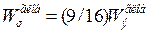 
. Таким образом, роль спина в случае 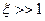возрастает.
Случай движения, соответствующий ультраквантовому приближению, может представить интерес для ряда задач астрофизики, в которых встречаются экстремально высокие энергии частиц, а также в условиях экстремально больших магнитных полей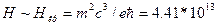 
Гс. Общее исследование возможности рассмотрения таких полей было проведено Гейзенбергом, причем им была доказана возможность решения задачи движения электрона в таком поле в виде одноэлектронной проблемы независимо от напряженности магнитного поля. В противоположность этому последовательная постановка одно-электронной задачи о движении частицы в электрическом поле возможна лишь при условии 
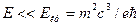. При поле Е, близком к критическому, становится возможным рождение пар и задача, таким образом, выходит за пределы одноэлектронного рассмотрения.
Задача о движении и излучении электрона в сверхсильном магнитном поле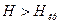 
впервые была рассмотрена В. Г. Багровым, О. Ф. Дорофеевым и И. М. Терновым. Особенностью этой задачи является характерная для этого случая дискретность энергетического спектра
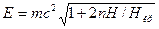(29)
(в предположении отсутствия движения вдоль поля: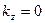 
).
Заметим, что спектр энергии электрона в магнитном поле не зависит от ориентации спина частицы: он вырожден по квантовому числу 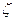. Вместе с тем при малых квантовых числах 
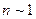спектр энергии электрона начинает иметь отличие от спектра бесспиновой частицы, поскольку энергия бозона (спин равен 0) имеет несколько иное по сравнению с (29) выражение
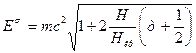
и в «основном» состоянии, когда я = 0 эти формулы отличаются друг от друга, в особенности при большой напряженности магнитного поля. Физически такое различие связано со спином частиц. Электрон (в отличие от бозона) обладает в магнитном поле таким квантовым состоянием (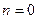 
), в котором орбитальный и спиновой моменты компенсируют друг друга. В этом состоянии спин электрона всегда направлен против магнитного поля.
Движение электрона в однородном магнитном поле имеет некоторую аналогию с проблемой водородного атома. Именно на это обстоятельство обратил внимание Шотт, пытавшийся объяснить дискретность излучения атомов на основе классической модели движения частицы.
Как следует из общих формул квантового радиуса движения частицы: 
, в «основном» ( 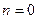) и первых возбужденных состояниях (п = 0, 1, 2... ) — низкие энергетические уровни — электрон движется по окружности, радиус которой определяется напряженностью магнитного поля. Для обычных полей 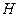~104 Гс окружность орбиты электрона имеет радиус ~10~5 см. Локализация частицы возрастает при полях порядка критического значения: 
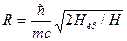, и окружность сжимается до радиуса порядка комптоновской длины волны 
.
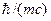Существенно, что в экстремально сильном магнитном поле электрон, находящийся даже на первом возбужденном уровне, является релятивистским, а его движение — квантовым.
В связи с изложенными, здесь замечаниями становится очевидным, что в отличие от рассмотренной нами теории СИ, справедливой для квазиклассического движения электрона (в предположении больших квантовых чисел), можно указать другую область значений энергии — область малых значений главного квантового числа. В сильном магнитном поле даже при условии малости числа п может реализоваться область релятивистского движения частицы. Для рассмотрения мощности СИ в этом случае избранная нами аппроксимация функций Лагерра с помощью функций Макдональда с индексом 1/3 становится непригодной, ибо она была основана на больших значениях главного квантового числа.
Пооведение вычислений в случае низких энергетических уровней, в особенности в предположении экстремально больших значений напряженности магнитного поля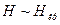 
, возможно лишь численными методами. При этом оказывается, что вероятность спонтанных переходов перестает зависеть от ориентации спина, причем переходы с изменением ориентации спина происходят с той же вероятностью, что и без изменения поляризации.
Мощность излучения 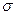- и 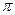- компонент линейной поляризаций принимает вид
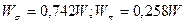
где
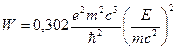(30)
Последняя формула может быть приведена к виду
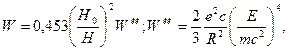(31)
откуда следует, что формула для мощности излучения W отличается от известной классической формулы умножением на инвариантную величину
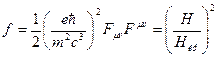
Полученное выражение для мощности не совпадает не только с результатами классической теории, но и с ультраквантовым случаем движения электрона в возбужденном состоянии в сверхсильном поле. Как видно из (30), (31), излучение электрона, находящегося на первых возбужденных уровнях, обладает существенными особенностями.
Список используемой литературы:
1. И. М. Тернов, В. В. Михайлин Синхротронное излучение. Теория и эксперимент.
Москва. Энегроатомиздат 1986 г.
2. А. А. Соколов, И. М. Тернов Релятивистский электрон.
Москва. Наука 1983 г.
3. А. А. Соколов, И. М. Тернов, В. Г. Багров, Р. А. Разаев Синхротронное излучение.
Москва. Наука 1966 г.
4. И. С. Данилкин, А. Н. Лебедев, Е. М. Морозова под ред. Б. Н. Яблокова
Москва. Госатомиздат. 1962 г.
|
|
|
