Квантовые состояния электрона в магнитном поле.

Квантовые состояния электрона в магнитном поле.

                           Волновая функция.

 

          Рассмотрим волновую функцию электрона, движущегося в постоянном и однородном магнитном поле, которое для определенности будем полагать направленным по оси 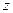цилиндрической системы координат. Тогда вектор-потенциал постоянного магнитного поля выберем в виде

 

       

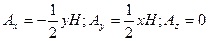
При этом

                

      ,

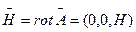И гамильтониан уравнения Дирака имеет выражение

              

     

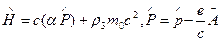
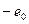Заряд электрона в дельнейшем полагаем , где .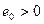

      Как известно, для определения состояний электрона необходимо задание четырех квантовых чисел -- трех, соответствующих движению в пространстве, и четвертого, определяющего внутреннюю степень свободы электрона, т. е. связанного со спином. Таким образом, для полного набора, характеризующего квантовое состояние частицы, нам необходимо выбрать четыре оператора, каждый из которых коммутирует с гамильтонианом и является интегралом движения. При этом все эти операторы будут иметь общую для них волновую функцию.

      В рассматриваемой задаче о движении электрона в магнитном поле можно потребовать, чтобы волновая функция была собственной для следующих операторов:

     1) энергии

                    

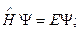
      2) проекции импульса на направление магнитного поля     

        

           

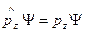
      3) проекции полного момента количества движения  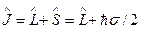на направление поля

 

     

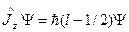
Для определения спинового состояния, т. е. разделения решений уравнения Дирака по спину, необходим четвертый оператор, коммутирующий с гамильтонианом, -- оператор поляризации. Но пока ограничимся рассмотрением решений уравнения Дирака без их разбиения по спину.

      В рассматриваемой стационарной задаче переменные в уравнении Дирака разделяются и волновую функцию 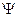 можно представить в виде

 

     

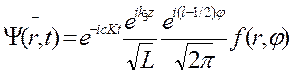
где 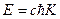 -- энергия электрона;  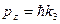-- импульс частицы, характеризующий движение вдоль магнитного поля;  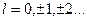-- азимутальное квантовое число;  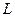-- длина периодичности. Детали вычисления матрицы 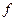опускаются, результат вычисления записывается в виде функции Лагерра

 

      )

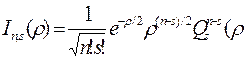где 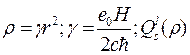 -- полином Лагерра,

 

 

      

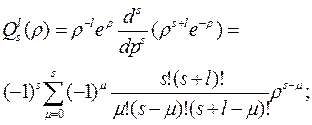
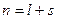 -- главное или энергетическое квантовое число, ;  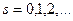-- радиальное число. Оба квантовых числа  и  принимают целые положительные значения. При этом матрица 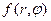 имеет вид

 

     

В этом выражении коэффициенты 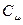 связаны уравнением Дирака:

 

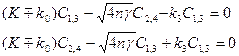            (1)

и условием нормировки 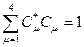; конкретный вид этих коэффициентов зависит от выбора оператора поляризации – четвертого оператора, определяющего квантовое состояние электрона. К этому вопросу будут даны пояснения ниже.

         Спектр энергии электрона

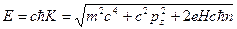         (2)

 определяется главным квантовым числом  и импульсом вдоль направления магнитного поля 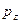, принимающего непрерывные значения. В случае макроскопического движения электрона главное квантовое число  принимает очень большие значения и спектр энергии является квазинепрерывным. В нерелятивистском приближении квантование периодического движения в плоскости, перпендикулярной к магнитному полю 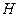, переходит в эквидистантный спектр (уровни Ландау)

 

       

         

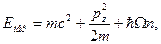
где 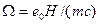-- циклотронная частота.

       Иное положение в случае сильных магнитных полей. Преобразуем выражение для энергии (1) к несколько другому виду и предположим, что движение вдоль поля отсутствует. Тогда получим выражение

 

        ,

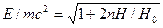Из которого видно, что при 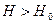 движение даже на низких уровнях ( 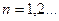) становится релятивистским, а спектр энергии существенно дискретным.

        Рассмотри подробнее физический смысл квантовых чисел, для этого найдем с помощью волновой функции квадратичную флуктуацию радиуса

 

         ;

  

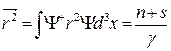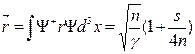             (3)

Вводя далее по общим правилам квадратичную флуктуацию радиуса (дисперсию), находим, что её значение определятся радиальным квантовым числом

 

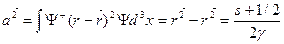           (4)

         Дадим теперь классическую интерпретацию полученных выводов. Как известно, в случае движения электрона в плоскости орбиты вращения энергия частицы и радиус орбиты связаны соотношением

 

             

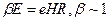
Чтобы установить связь радиуса 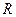с квантовыми числами, рассмотрим движение электрона по окружности радиусом 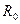, центр которой не совпадает с началом координат. Пусть расстояние от центра окружности до центра координат равно  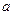(рис. 1). Тогда среднее по углу  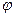значение квадрата радиуса будет равно:

 

           

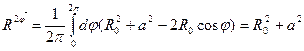
Сравнивая это выражение с (3), находим, что

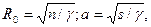                              (5)

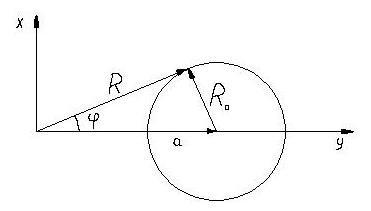
                            Рис. 1

т. е. радиус определяется главным квантовым числом, а радиальное квантовое число характеризует расстояние центра траектории от начала координат.

       Из сравнения (4) и (5) следует также связь a и квадратичной флуктуации радиуса

          

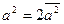
Исходя из полученных формул, можно дать объяснение пределов изменения азимутального квантового числа 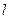. Действительно, находим

    

         

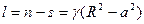
т. е. положительные значения 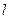соответствуют тому, что начало координат, находится внутри окружности 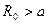, а отрицательные – вне её ( 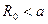). В дальнейшем ограничимся рассмотрением случая, когда центр окружности, по которой происходит движение частицы, близок к началу координат, т. е. 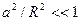. При этом естественно ограничиться положительными значениями орбитального квантового числа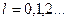

        Из выражения для радиуса орбиты вращения электрона вид­но, что в случае экстремально сильных полей 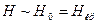проис­ходит сильная локализация частицы в плоскости орбиты враще­ния

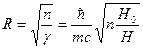 (6)

В этом можно убедиться исходя из вида волновой функции. Плотность вероятности ради- ального распределения элект­рона будет определяться функциями Лагерра, которые в случае низких уровней энергии ( ~1) пропорциональны экспо­ненте 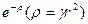. Отсюда следует, что область пространственной локализации электрона имеет порядок , т. е. вновь получа­ется результат (7) (ультраквантовая область движения ча­стицы).

Таким образом, основное и низшие возбужденные состояния электрона в сверхсильном магнитном поле 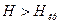сильно локали­зованы— волновой пакет, описывающий движение частицы в пло­скости, перпендикулярной магнитному полю, имеет характерный размер порядка комптоновской длины волны, а при 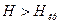даже меньше ее. Вследствие этого в полях порядка экстремального поля вещество ведет себя необычным образом. Так, например, резко изменяются свойства атомов: атом водорода деформируется в сильном магнитном поле, приобретая игольчатую форму, — он сильно вытянут вдоль направления поля, поскольку его харак­терный размер вдоль поля остается равным 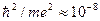см, а в плоскости, перпендикулярной полю Н, локализация электрона сжи­мает атом до размеров порядка см.

В обычных условиях движения частицы в ускорителе или на­копительном кольце магнитное поле 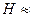10⁴ Гс, а радиус орбиты электрона — десятки и сотни метров. При этом квантовое число п принимает очень большие значения и спектр энергии становится квазинепрерывным. Так, в частности, для Н =10⁴ Гс и 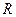= 100 м ~10¹⁸ — движение квазиклассическое. Полученные решения урав­нения Дирака достаточно строго описывают все слу­чаи движения электрона, включая и ультраквантовую и квазиклас­сическую области. Это открывает широкие возможности для иссле­дования квантовых эффектов, включая макроскопическую область движения частицы.

 

 

      

 

          Разделение решений уравнения Дирака по

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: