 |
Приложение теории комплексных чисел к решению уравнений
|
|
|
|
3- и 4-й степени
Рассмотрим решение кубического уравнения
 (1)
(1)
на конкретном примере.
Пример 1. Решите уравнение
 .
.
Решение. Приведем сначала наше уравнение к уравнению, не содержащему квадрат неизвестной (такое уравнение называется приведенным), т.е. к уравнению вида:
 ,
,
для чего произведем подстановку:

Получим уравнение:
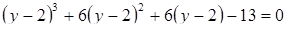 .
.
Раскрыв скобки и приведя подобные члены, приходим к уравнению:
 ,
,
где  ,
,  и
и 
(Замечание.
Переход к приведенному кубическому уравнению можно осуществить с помощью схемы Горнера, разложив многочлен  по степеням двучлена
по степеням двучлена  )
)
Для корней кубического уравнения
 (2)
(2)
имеется так называемая формула Кардано, хотя правильнее было бы ее называть формулой дель Ферро – Тартальи - Кардано.
Впервые приведенное кубическое уравнение

решил профессор Болонского университета Сципион дель Ферро в конце XV века. Затем в 1535 году те же формулы были выведены Николо Тартальей. Наконец, в 1545 году решение уравнения (1) было изложено в книге Джероламо Кардано "Ars Magna" ("Великое искусство").
Формулы Кардано имеют вид:
 ,
, 
где  – значения радикала
– значения радикала


Практически корни  находятся проще.
находятся проще.
Пусть  – одно (любое) значение радикала u. Тогда два других значения можно найти следующим образом:
– одно (любое) значение радикала u. Тогда два других значения можно найти следующим образом:
 ;
; 
где e1 и e2 – значения корня кубического из 1, т.е.


Если вычислить  то получим:
то получим:
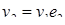 ;
; 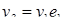 .
.
Действительно,
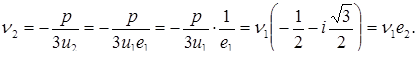
Аналогично доказывается равенство  .
.
Подставляя полученные значения  и
и  в формулу
в формулу
 ,
, 
находим практические формулы:

 ;
;
 ;
;
 .
.
В нашем случае:

Таким образом, положим  . Тогда
. Тогда

следовательно,
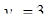 ,
,  ,
, 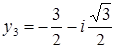 .
.
Из последних равенств, учитывая, что  получаем:
получаем:
 ,
,  ,
,  .
.
Ответ:  ;
;  ;
;  .
.
Для приведенного кубического уравнения
 (3)
(3)
дискриминант вычисляется по формуле:
|
|
|
 .
.
При этом:
а) если  , то уравнение (3) имеет один действительный и два комплексно сопряженных корня;
, то уравнение (3) имеет один действительный и два комплексно сопряженных корня;
б) если  , то уравнение (3) имеет три действительный корня, два из которых равны;
, то уравнение (3) имеет три действительный корня, два из которых равны;
в) если  , то уравнение (3) имеет три различных действительный корня.
, то уравнение (3) имеет три различных действительный корня.
Таким образом, в любом случае уравнение (3) с действительными коэффициентами имеет хотя бы один действительный корень.
Рассмотрим решение уравнения 4-й степени методом Феррари на конкретном примере.
Пример 2. Решите уравнение

Решение.
Оставим в левой части уравнения члены, содержащие  и
и  :
:
 .
.
Дополним левую часть полученного уравнения до полного квадрата:
 ,
,
или
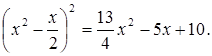 (1)
(1)
Введем в полный квадрат левой части равенства (1) параметр r:

Откуда с учетом равенства (1) получим:
 (2)
(2)
Подберем значение параметра r таким образом, чтобы дискриминант правой части равенства (2) обратился в нуль (т.е. чтобы в правой части равенства (2) также получился полный квадрат).

Дискриминант D равен нулю тогда и только тогда, когда число r является корнем уравнения:
 ;
;
 .
.
В частности,  , если
, если  .
.
Подставив значение  в равенство (2), получим:
в равенство (2), получим:
 ,
,
или
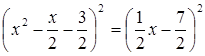 .
.
Откуда,
 ,
,
 ,
,
 или
или  .
.
Следовательно,
 ;
;  ;
;
 ;
; 
Ответ:  ;
;  ;
;  ;
; 
Задача 69. Решите уравнение  .
.
Решение
Данное уравнение – приведенное. Здесь  ,
,  . Следовательно,
. Следовательно,
 .
.
Для извлечения кубического корня из комплексного числа 
представим его в тригонометрической форме:
 ,
,
поэтому  , где
, где 
При  получаем:
получаем:
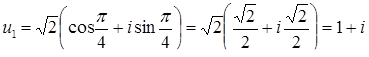 .
.
Значит,
 ,
,
поэтому  .
.
Следовательно,
 ,
,  ,
,  .
.
Ответ: 2;  ;
; 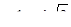 .
.
Задача 70. Решите уравнение  .
.
Решение
Положив  , получаем приведенное уравнение относительно неизвестной переменной y:
, получаем приведенное уравнение относительно неизвестной переменной y:
 .
.
По формулам Кардано:
 .
.
Легко видеть, что  .
.
Следовательно, число  является одним из значений кубического
является одним из значений кубического
корня из комплексного числа  (тот же результат получается, если применить формулу извлечения корня n-й степени из комплексного числа).
(тот же результат получается, если применить формулу извлечения корня n-й степени из комплексного числа).
Таким образом,  ,
,  , тогда
, тогда
|
|
|
 ,
,  .
.
Итак, 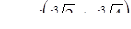 ,
,
 ,
,
 .
.
Отсюда находим корни квадратного уравнения:
 ,
,
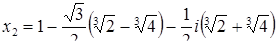 ,
,
 .
.
Ответ:  ;
;  ;
;
 .
.
Задача 71. Не решая следующие уравнения, определите характер корней каждого их них:
а)  ;
;
б)  ;
;
в)  .
.
Решение.
а)  .
.
Дискриминант  , т.е.
, т.е.  , то уравнение имеет один действительный и два комплексно сопряженных корня.
, то уравнение имеет один действительный и два комплексно сопряженных корня.
б)  .
.
Переходя к приведенному кубическому уравнению, получаем:
 (б*). Откуда дискриминант
(б*). Откуда дискриминант 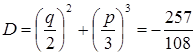 , т.е.
, т.е.  , то уравнение (б*), а, значит, и (б) имеет три различных действительный корня.
, то уравнение (б*), а, значит, и (б) имеет три различных действительный корня.
в)  .
.
Переходя к приведенному кубическому уравнению, получаем:  (в*). Отсюда
(в*). Отсюда  ,
,  , то уравнение (в*), а, значит, и уравнение (в) имеет один действительный и два комплексно сопряженных корня.
, то уравнение (в*), а, значит, и уравнение (в) имеет один действительный и два комплексно сопряженных корня.
Ответ: а) один действительный и два комплексно сопряженных корня; б) три различных действительный корня; в) один действительный и два комплексно сопряженных корня.
Задача 72. Решите уравнения: а) 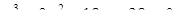 ;
;
б)  .
.
Решение.
а) 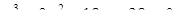 .Переходя к приведенному кубическому уравнению с помощью подстановки
.Переходя к приведенному кубическому уравнению с помощью подстановки  , получим уравнение:
, получим уравнение:
 , где
, где  ,
,  .
.
Зная, что:
 ;
;
 ;
;
 .
.
По формулам Кардано:


Таким образом, получаем  , значит
, значит  ,
,  ,
, 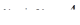 ,
,  .
.
Следовательно,  ;
;  ;
;  .
.
Откуда, 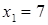 ,
,  ,
,  .
.
б)  .
.
Переходить к приведенному кубическому уравнению не нужно, так как исходное уравнение само является приведенным, причем  ,
,  .
.
Таким образом, получаем:  ,
,  .
.
Тогда  ,
,  ,
,  ,
,  .
.
Следовательно,  ,
,  .
.
Ответ: а) 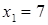 ,
,  ,
,  ;
;
б)  ,
,  .
.
Задача 73. Решите уравнения: а)  ;
;
б)  .
.
Решение.
а) Преобразуем уравнение  (а) по методу Феррари:
(а) по методу Феррари:  ,
,
 ,
,
 . (а*)
. (а*)
Введем в полный квадрат левой части равенства параметр r:

Откуда с учетом равенства (а*) находим:
 ,
,
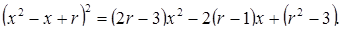 (а**).
(а**).
Теперь подберем такое значение параметра r, чтобы дискриминант
правой части равенства (а**) обратился в нуль.

Дискриминант D равен нулю тогда и только тогда, когда число r является корнем уравнения:
 ;
;
 ;
;
 .
.
В частности,  , если
, если  .
.
Подставив найденное значение  в равенство (а*), получим:
в равенство (а*), получим:
 , или
, или  .
.
Откуда,  ,
,
 ,
,
 или
или  .
.
Следовательно,  ;
;  ;
;  ;
;  .
.
б)  .
.
Преобразуем это уравнение по методу Феррари:
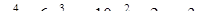 ,
,
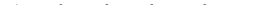 ,
,
 . (б*)
. (б*)
Введем в полный квадрат левой части равенства параметр r:

Откуда с учетом равенства (б*) находим:
 (а**).
(а**).
Подберем такое значение параметра r, чтобы дискриминант квадратного трехчлена в правой части равенства (а**) обратился в нуль.

Легко видеть, что дискриминант D равен нулю, если  . следовательно, подставив значение
. следовательно, подставив значение  в равенство (б**), получим:
в равенство (б**), получим:
|
|
|
 ;
;
 .
.
Откуда,  ,
,
 или
или  .
.
Следовательно,
 ;
;  ;
;  ;
;  .
.
Ответ: а)  ;
;  .
.
б)  ; 3; 1.
; 3; 1.
|
|
|


