 |
Комплексные числа и параметры
|
|
|
|
«Параметр (от греч. 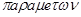 - отмеривающий) величина, значения которой служат для различения элементов некоторого множества между собой.
- отмеривающий) величина, значения которой служат для различения элементов некоторого множества между собой.
Например, уравнение 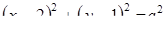 , где а > 0, х
, где а > 0, х  R, y
R, y  R, задает множество всех концентрических окружностей, с центром (2; 1) радиуса а (рис. 33).
R, задает множество всех концентрических окружностей, с центром (2; 1) радиуса а (рис. 33).

Рис. 33.
Если а = 1, то получим окружность 1), если а = 2, то - окружность 2) и т.д.
Интересно и следующее определение параметра «Неизвестные величины, значения которых задаем мы сами, называются параметрами».
Пусть, например, нужно решить уравнение
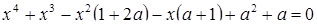 . Вряд ли легко мы справимся с этим уравнением, если будем решать относительно x, считая a параметром.
. Вряд ли легко мы справимся с этим уравнением, если будем решать относительно x, считая a параметром.
Лучше сначала считать х параметром и решать квадратное относительно а уравнение  , а затем поменять x и a ролями.
, а затем поменять x и a ролями.
Получим  Остается решить два уравнения
Остается решить два уравнения 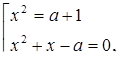 что труда уже не составит.
что труда уже не составит.
Прежде, чем перейти к решению задач, содержащих комплексные числа и параметр, сформулируем определения основных понятий, связанных с уравнениями (неравенствами) с параметром.
Определение 1. Пусть дано равенство с переменными x и a:  . Если ставится задача для каждого действительного значения, а решить это уравнение относительно x, то уравнение
. Если ставится задача для каждого действительного значения, а решить это уравнение относительно x, то уравнение  называется уравнением с переменной x и параметром a.
называется уравнением с переменной x и параметром a.
Параметр обычно обозначается первыми буквами латинского алфавита: а, b, с, d...
Переменная, относительно которой решается уравнение последними буквами латинского алфавита: x, у, z, t, и, v.
Определение 2. Под областью определения уравнения  с параметром а будем понимать все такие системы значений х и а, при которых
с параметром а будем понимать все такие системы значений х и а, при которых 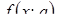 имеет смысл.
имеет смысл.
Иногда область определения уравнения устанавливается довольно легко, а иногда в явном виде это сделать трудно. Тогда ограничиваемся только системой неравенств, множество решений которой и является областью определения уравнения.
|
|
|
Определение З. Под решением уравнения  c параметром a будем понимать систему значений x и a области определения уравнения, обращающую его в верное числовое равенство.
c параметром a будем понимать систему значений x и a области определения уравнения, обращающую его в верное числовое равенство.
Определение 4. Решить уравнение  с параметром a - это значит, для каждого действительного значения a найти все решения данного уравнения или установить, что их нет.
с параметром a - это значит, для каждого действительного значения a найти все решения данного уравнения или установить, что их нет.
Определение 5. Уравнения  и
и 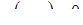 равносильны при фиксированном значении а = а0, если уравнения без параметра
равносильны при фиксированном значении а = а0, если уравнения без параметра  и
и 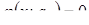 равносильны.
равносильны.
Определение 6. Уравнение 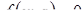 является следствием уравнения
является следствием уравнения 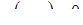 при некотором значении a=а0, если множество решений уравнения
при некотором значении a=а0, если множество решений уравнения 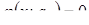 содержится среди множества решений уравнения
содержится среди множества решений уравнения  .
.
Задача 74. Определите семейство линий в комплексной плоскости, заданных уравнениями:
а) 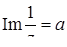 ; б)
; б) 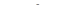 .
.
Решение
а) 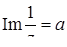 . О.О.У.:
. О.О.У.: 
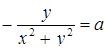 ,
, 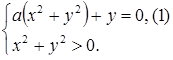
Решаем уравнение (1).
1) Пусть 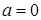 :
: 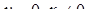 получим уравнение оси абсцисс, исключая начало координат.
получим уравнение оси абсцисс, исключая начало координат.
2) 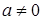 :
: 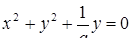 ,
, 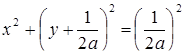 . Это семейство концентрических окружностей с центром в точке
. Это семейство концентрических окружностей с центром в точке 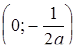 радиуса
радиуса 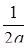 .
.
б)  .
.
Пусть  , тогда
, тогда  . И
. И 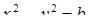 .
.
1) Если  , то полу чаем семейство из двух прямых с уравнениями
, то полу чаем семейство из двух прямых с уравнениями  и
и  .
.
2) Если 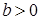 , то – семейство равносторонних гипербол с уравнениями
, то – семейство равносторонних гипербол с уравнениями 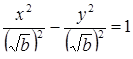 , с вершинами в точках
, с вершинами в точках  ,
, 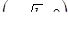 и асимптотами
и асимптотами  и
и  .
.
3) Если  , то – семейство равносторонних гипербол с уравнениями
, то – семейство равносторонних гипербол с уравнениями
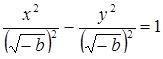 , с вершинами в точках
, с вершинами в точках 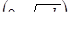 ,
,  и асимптотами
и асимптотами  и
и  .
.
Ответ: а) 1. Если 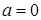 , то – уравнение оси абсцисс, исключая точку
, то – уравнение оси абсцисс, исключая точку  .
.
2. Если 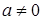 , то – семейство концентрических окружностей с центром в точке
, то – семейство концентрических окружностей с центром в точке 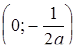 радиуса
радиуса 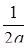 .
.
б) 1. Если  , то – семейство из двух прямых с уравнениями
, то – семейство из двух прямых с уравнениями  и
и  .
.
2. Если 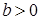 , то – семейство равносторонних гипербол с уравнениями
, то – семейство равносторонних гипербол с уравнениями 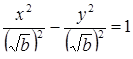 , с вершинами в точках
, с вершинами в точках  ,
, 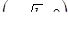 и асимптотами
и асимптотами  и
и  .
.
3. Если  , то – семейство равносторонних гипербол с уравнениями
, то – семейство равносторонних гипербол с уравнениями  , с вершинами в точках
, с вершинами в точках 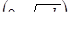 ,
, 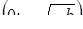 и асимптотами
и асимптотами  и
и  .
.
Задача 75. При каких значениях n верно равенство 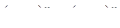 .
.
Решение
Тригонометрическими формами записи комплексных чисел 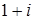 и
и 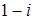 , являются
, являются 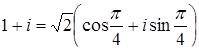 и
и  .
.
|
|
|
Возведем в степень n, получим 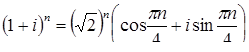 и
и  .
.
Тогда:
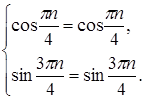
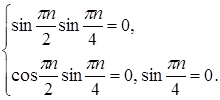
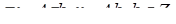
Ответ: 
Задача 76. При каком значении d 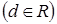 уравнением
уравнением  задана ось ординат в комплексной плоскости, исключая начало координат?
задана ось ординат в комплексной плоскости, исключая начало координат?
Решение
О.О.У.: 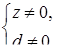
Пусть  . Тогда
. Тогда  .
.
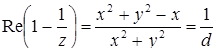 .
.
 ,
, 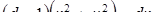 .
.
Если  , то получим уравнение
, то получим уравнение 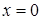 .
.
Ответ:  .
.
Задача 77. Среди всех комплексных чисел z таких, что 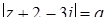 , где
, где 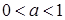 , есть ровно одно число, аргумент которого равен
, есть ровно одно число, аргумент которого равен 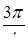 . Найдите это число.
. Найдите это число.
Решение
Запишем искомое число в тригонометрической форме:
 . Тогда
. Тогда  и
и  .
.
Перейдем к уравнению 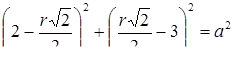 , где
, где 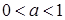 . Получаем квадратное уравнение
. Получаем квадратное уравнение 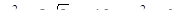 , где
, где 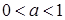 ,
,  .
.
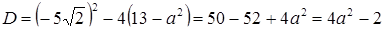 .
.
Рассмотрим 2 случая:
1.  :
:  ,
,

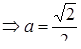 . Тогда
. Тогда 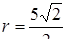 и
и  .
.
2. 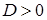 :
:
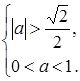
 .
.
Введем функцию  . Интересует случай, когда один из корней квадратного трехчлена больше 0, а другой – меньше 0 (Рис. 34).
. Интересует случай, когда один из корней квадратного трехчлена больше 0, а другой – меньше 0 (Рис. 34).

Рис. 34.
Достаточно решить систему неравенств: 

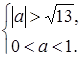 Эта система несовместна, поэтому такой случай невозможен.
Эта система несовместна, поэтому такой случай невозможен.
Ответ:  .
.
Задача 78. При каких действительных значениях a среди комплексных чисел  таких, что
таких, что 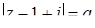 , нет ни одного числа, модуль которого равен 2.
, нет ни одного числа, модуль которого равен 2.
Решение
Комплексное число  с модулем
с модулем  запишется так:
запишется так:  .
.
Тогда 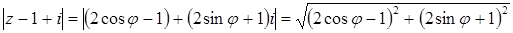 .
.
Получим уравнение  .
.
1.Если 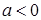 , то уравнение действительных решений не имеет.
, то уравнение действительных решений не имеет.
2.Пусть 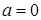 :
:


Решая систему методом «лепестков» (Рис. 35), видим, что она несовместна.
Рис. 35.
3.  :
: 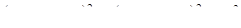 ,
,
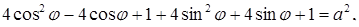


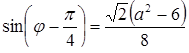 .
.
Последнее уравнение не имеет корней, если a удовлетворяет системе:
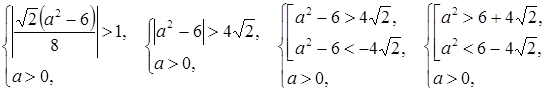
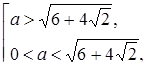
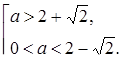
Изобразим графически решение в данных случаях (рис. 36).

Рис. 36.
Ответ:  .
.
Задача 79. Для каждого действительного числа a найдите все комплексные числа  , удовлетворяющие равенству: а)
, удовлетворяющие равенству: а) 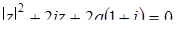 ;
;
б)  .
.
Решение
а) Пусть 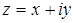 , тогда из исходного уравнения имеем
, тогда из исходного уравнения имеем 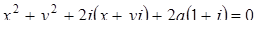 .
.
Отсюда получаем систему для нахождения x и y:
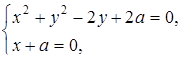
из которой следует, что 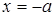 . Подставляя это значение x в первое уравнение, имеем
. Подставляя это значение x в первое уравнение, имеем 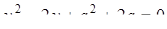 . Корни этого уравнения действительны тогда и только тогда, когда его дискриминант является действительным числом, т. е.
. Корни этого уравнения действительны тогда и только тогда, когда его дискриминант является действительным числом, т. е. 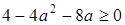 . Для этих значений a найдем
. Для этих значений a найдем 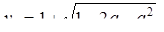
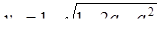 причем
причем  , то
, то 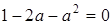 . Неравенство
. Неравенство 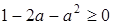 выполняется для всех a из промежутка
выполняется для всех a из промежутка  . Таким образом, исходное уравнение при
. Таким образом, исходное уравнение при  имеет два корня:
имеет два корня: 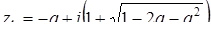 ,
, 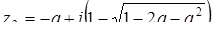 при
при  решений не имеется.
решений не имеется.
б) Перепишем данное уравнение в виде  . Так как
. Так как  и a – действительные числа, то отсюда заключаем, что число z является чисто мнимым числом.
и a – действительные числа, то отсюда заключаем, что число z является чисто мнимым числом.
Пусть  , тогда из исходного уравнения находим, что
, тогда из исходного уравнения находим, что  , т. е.
, т. е.  .
.
Последнее уравнение равносильно совокупности двух систем:
|
|
|
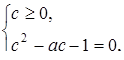
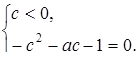
Уравнение 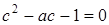 имеет два корня:
имеет два корня:  при любом значении a. Неравенству
при любом значении a. Неравенству  удовлетворяет (при любом значении a) только число
удовлетворяет (при любом значении a) только число 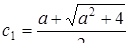 .
.
Уравнение  второй системы совокупности имеет действительные решения только при условии
второй системы совокупности имеет действительные решения только при условии  , т. е. при
, т. е. при 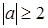 . Корнями этого уравнения при каждом
. Корнями этого уравнения при каждом 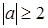 являются числа
являются числа  .
.
Ясно, что при  оба корня
оба корня  и
и  меньше нуля, а при
меньше нуля, а при 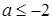 – больше нуля.
– больше нуля.
Таким образом, исходное уравнение:
при 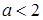 имеет один корень
имеет один корень 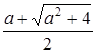 ;
;
при  имеет три корня
имеет три корня 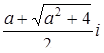 ,
, 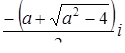 ,
, 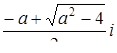 .
.
Ответ: а) при  , то
, то 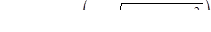 ,
, 
б) при 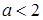 , то
, то 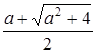 ;
;
при  , то
, то 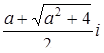 ,
, 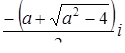 ,
, 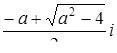 .
.
Задача 80. Для каких действительных чисел a не существует комплексных чисел z, для которых выполняются равенства 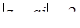 ,
, 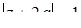 ?
?
Решение
Заметим, что  равняются расстоянию между точками
равняются расстоянию между точками 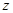 и
и 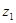 на комплексной плоскости. При фиксированном a точки
на комплексной плоскости. При фиксированном a точки  , для которых
, для которых 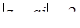 , лежат на окружности с центром в
, лежат на окружности с центром в 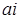 и радиусом 2. (Вообще, множество
и радиусом 2. (Вообще, множество  , для которых
, для которых  , есть окружность с центром в
, есть окружность с центром в  и радиусом
и радиусом 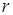 ). Аналогично равенство
). Аналогично равенство 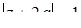 . Две окружности не имеют общих точек, если расстояние между их центрами больше суммы или меньше разности радиусов. Таким образом, должно выполняться одно из двух неравенств:
. Две окружности не имеют общих точек, если расстояние между их центрами больше суммы или меньше разности радиусов. Таким образом, должно выполняться одно из двух неравенств: 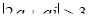 или
или 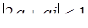 , т.е.
, т.е. 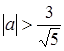 или
или 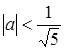 .
.
Ответ: 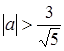 или
или 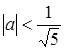 .
.
Задача 81. При каких действительных чисел a любое комплексное число, удовлетворяющее уравнению  , удовлетворяет одновременно и неравенству
, удовлетворяет одновременно и неравенству  ?
?
Решение
Пусть 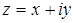 . Тогда
. Тогда 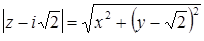 и получим уравнение
и получим уравнение
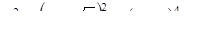
Если 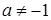 , то имеем уравнение окружности с центром в точке
, то имеем уравнение окружности с центром в точке  и
и
 . От неравенства
. От неравенства  перейдем к неравенству
перейдем к неравенству
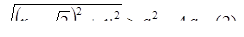
Рассмотрим ряд случаев в зависимости от значений a.
1.  , т.е.
, т.е. 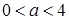 . Неравенство (2) выполняется при любых парах действительных значений x и y, в том числе и при решениях уравнения (1).
. Неравенство (2) выполняется при любых парах действительных значений x и y, в том числе и при решениях уравнения (1).
2. Пусть 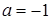 :
:

Система решений не имеет.
3.Если 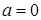 , то получим систему
, то получим систему

Неравенству системы удовлетворяют все пары значений x и y (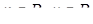 ), кроме
), кроме  – не является решением уравнения системы.
– не является решением уравнения системы.
4.Аналогично убеждаемся, что условию задачи удовлетворяет и  .
.
5.Остается рассмотреть следующее множество значений a: 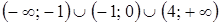 .
.
В этом случае  и неравенство (2) задает множество точек комплексной плоскости, расположенных вне окружности, заданной уравнением
и неравенство (2) задает множество точек комплексной плоскости, расположенных вне окружности, заданной уравнением  . (3) (Рис. 37).
. (3) (Рис. 37).
Обозначим радиус этой окружности через r (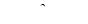 ). И достаточно найти такие значения a из рассматриваемого множества, при которых окружность, заданная уравнением (1), расположена вне окружности с уравнением (3).
). И достаточно найти такие значения a из рассматриваемого множества, при которых окружность, заданная уравнением (1), расположена вне окружности с уравнением (3).
|
|
|
Рассмотрим прямоугольный треугольник 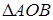 :
: 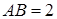 ;
;  ;
; 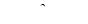 ;
; 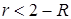 .
.

Рис. 37.
Получим неравенство 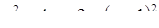 .
.
 ,
, 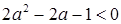 , т.о.
, т.о. 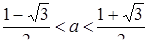 .
.
Учтем множество значений a, на котором мы решаем систему (рис. 38):

Рис. 38.
Таким образом, 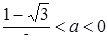 .
.
Ответ:  .
.
Задача 82. Найдите все действительные a такие, что система уравнений  не имеет решений.
не имеет решений.
Решение
1. Если 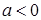 , то решений нет.
, то решений нет.
2. При 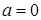 ,
,  .
.
3. Если  :
:
Каждое из данных уравнений задает на комплексной плоскости окружность. Пусть О1 и О2 – центры этих окружностей, r1 и r2 – соответствующие радиусы.
Если расстояние между их центрами  удовлетворяют условиям
удовлетворяют условиям 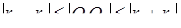 , то окружности имеют хотя бы одну общую точку. тогда получим систему неравенств
, то окружности имеют хотя бы одну общую точку. тогда получим систему неравенств

Поэтому при  система решений не имеет.
система решений не имеет.
Ответ: 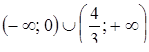 .
.
Заключение
В представленной выпускной квалификационной работе получены следующие результаты.
1) Приведено систематическое изложение вопроса решения задач с комплексными числами.
2) Приведены решения задач с комплексными числами в алгебраической форме, вычисление операций сложения, вычитания, умножения, деления, операции сопряжения для комплексных чисел в алгебраической форме, степень мнимой единицы, модуль комплексного числа, а также изложено правило извлечения квадратного корня из комплексного числа.
3) Решены задачи, посвященные геометрической интерпретации комплексных чисел в виде точек или векторов комплексной плоскости;
4) Рассмотрены действия над комплексными числами в тригонометрической форме.
5) Приведены решения некоторых уравнений 3-й и 4-й степеней;
6) Решены некоторые задачи содержащие комплексные числа и параметры.
Материал, изложенный в выпускной квалификационной работе может быть использован в учебном процессе в курсе алгебры в высшем учебном заведении, а также в классах с углубленным изучением математики или на элективных курсах в школе.
Список литературы
1. Абрамов А.М., Виленкин Н.Я., Дорофеев Г.В., Егоров А.А., Земляков А.Н., Моркович А.Г. Избранные вопросы математики. 10 класс. Факультативный курс. – М.: Просвещение, 1980.
2. Алгебра: Учеб. для 8 кл. общеобразоват. учреждений/ Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др. – 7-е изд. – М.: Просвещение, 2000.
3. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В., Шабунин М.Ш. Алгебра и начала анализа. Пробный учебник 9-10 классов средней школы. – М.: Просвещение, 1975.
4. Андронов И.К. Математика действительных и комплексных чисел. – М.: Просвещение, 1975.
5. Беляева Э.С., Потапов А.С. Уравнения и неравенства первой степени с параметром и к ним сводимые. Учебное пособие. – Воронеж: ВГПУ, 2001.
|
|
|
6. Болтянский В.Г., Сидоров Ю.В., Шабунин М.И. Лекции и задачи по элементарной математике. - М.: Наука, 1971.
7. Вавилов В.В, Мельников И.И., Олехник С.Н., Пасиченко П.И. Задачник по математике. Алгебра. Справочное пособие. – М.: Наука, 1987.
8. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 11 класса: Учебное пособие для учащихся школ и классов с углубленным изучением математики.– 6-е изд. – М.: Просвещение, 1998.
9. Галицкий М.А., Мошкович М.М., Шварцбурд С.И. Углубленное изучение курса алгебры и математического анализа. – М.: Просвещение, 1989.
10. Гордиенко Н.А., Беляева Э.С., Фирстов В.Е., Серебрякова И.В. Комплексные числа и их приложения: Учебное пособие. – Воронеж: ВГПУ, 2004.
11. Дадаян А.А., Новик И.А. Алгебра и начала анализа. – М.: Просвещение, 1987.
12. Звавич Л.И. и др. Алгебра и начала анализа. Решение задач письменного экзамена. / Л.И. Звавич, Л.Я. Шляпочник, И.И. Кулагина. – М.: Дрофа, 2000.
13. Карп А.П. Сборник задач по алгебре и началам анализа. Учебное пособие для учащихся школ и классов с углубленным изучением математики.– М.: Просвещение, 1995.
14. Математика в школе. № 3, 1990.
15. Математика в школе. № 6, 1992.
16. Окунев Л.Я. Высшая алгебра. – М.: Просвещение, 1966.
17. Петраков И.С. Математические кружки в 8 – 10 классах. – М.: Просвещение, 1988.
18. Фадеев Д.К., Никулин М.С., Соколовский И.Ф. Элементы высшей математики для школьников. – М.: Наука, Главная редакция физико-математической литературы, 1987.
19. Цыпкин А.Г., Пинский А.И. Справочник по методам решения задач по математике для средней школы. – М.: Наука, 1989.
20. Шарыгин И.Ф. Факультативный курс по математике: Решение задач: учебное пособие для 10 классов средней школы. – М.: Просвещение, 1989.
21. Шклярский Д.О., Ченцов Н.Н., Яглом И.М. Избранные задачи и теоремы элементарной математики. Арифметика и алгебра. – М.: Физматлит, Лаборатория Базовых Знаний, 2001.
22. Энциклопедический словарь юного математика. (Составитель Савин А.П.). – М.: Педагогика, 1989.
23. Яглом И.М. Комплексные числа и их приложения в геометрии. Изд. 2-е, стереотипное. – М.: Едиториал УРСС, 2004.
|
|
|


