Вимоги до оформлення. Рис. 1. Структурна схема систем передачі інформації. Варіанти домашнього завдання. Примітка. Методичні рекомендації до виконанню домашнього завдання

Вимоги до оформлення

1. Домашнє завдання слід виконувати на окремих аркушах формату А4.

2. Розрахунки системи передачі інформації проводити, використовуючи програмне забезпечення MathCad .

3. Варіант завдання вказувати на титульному аркуші домашнього завдання.

 

Рис. 1. Структурна схема систем передачі інформації

 

На рис. 1 введено такі позначення:

ДП – джерело неперервного повідомлення;

АЦП – аналого-цифровий перетворювач, перетворює повідомлення у відліки a(t_i), квантовані рівні a_j(t_i) і у відповідні їм числа j(t_i) – номера рівнів;

К – кодер, виконує кодування й утворює модулюючий сигнал b(t);

М – модулятор, утворює високочастотний аналоговий сигнал s(t);

НК – неперервний канал, на виході якого утворюється адитивна суміш сигналу z(t) з перешкодою;

ДМ – демодулятор, відновлює передані кодові символи b_к;

ДК – декодер, відновлює номера переданих рівнів  j(t_i);

ЦАП – цифроаналоговий перетворювач, відновлює квантовані рівні a_j(t_i) і неперервне повідомлення a(t);

ОП – одержувач повідомлень.

Варіанти домашнього завдання

Номер варіанта	amax, В	fв, Гц	J	N0, В2/Гц
	3, 6	6, 2·106		5, 25•10-10
	4, 0	5, 6•106		7, 22•10-10
	3, 6	5, 7•105		5, 24•10-10
	3, 2	6, 3•105		7, 26•10-10
	4, 2	5, 7•106		7, 29•10-10
	4, 0	6, 2•105		7, 84•10-10
	3, 2	6, 4•105		6, 27•10-10
	3, 6	6, 7•106		7, 28•10-10
	3, 6	6, 4•105		7, 44•10-10
	3, 2	6, 0•106		7, 24•10-10

Примітка.

 j – рівень сигналу на вході АЦП.

 

МЕТОДИЧНІ РЕКОМЕНДАЦІЇ ДО ВИКОНАННЮ ДОМАШНЬОГО ЗАВДАННЯ

 

Джерело повідомлення

Для розрахунку маємо випадковий процес – неперервний за часом сигнал, основна потужність якого зосереджена у всьому діапазоні частот від 0 до f_в. Миттєві значення сигналу рівноймовірні в інтервалі від a_min до a_max(розподілені за рівномірним законом). Щільність імовірності (рис. 2. ) має вигляд:

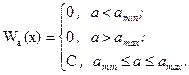
Рис. 2. Щільність розподілу W_a(x) миттєвих значень повідомлення a(t)

 

C визначається за умови нормування:

;                                     

.

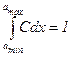Інтегральна функція розподілу (рис. 3. ) F_a(x) миттєвих значень повідомлення a(t)

,                              

отже,

;                  

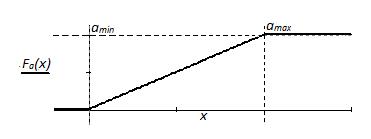
Рис. 3. Графік інтегральної функції F_a(x)

 

Математичне сподівання M процесу a(t):

.              

Дисперсія D процесу a(t):

            

Постійна складова процесу a(t):

.

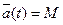Потужність змінної складової P_a:

P_a = D;

.

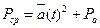Спектральна щільність потужності P_a (рис. 4. ) має рівномірний розподіл в інтервалі частот від 0 до F_в величиною N_a. Тоді:

;

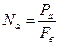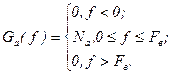
Рис. 4. Графік спектральної щільності середньої потужності

 

Визначимо диференціальну ентропію:

.

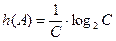Аналого-цифровий перетворювач

Передача інформації здійснюється з використанням дискретної системи зв'язку. Для цього повідомлення a(t) аналого-цифровим перетворювачем дискретизується за часом і квантується за рівнем.

Визначимо інтервал дискретизаціі 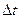 за теоремою Котельнікова:

.

Визначимо кількість рівнів квантування L, потрібних для заміни будь-якого неперервного відліку a(t_i) квантованим відліком

;

.

Оскільки миттєві значення рівноймовірні в заданому інтервалі, то закон розподілу шуму W(ξ ) в інтервалі a_j-Δ a/2 ≤ ξ ≤ a_j+Δ a/2 буде рівноймовірним і не залежатиме від номера інтервалу.

Отже, середня потужність шуму квантування буде дорівнювати:

.

Закон розподілу шуму визначимо з умов нормування:

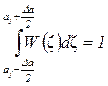 G_a(f)  F_v N_a  4f

 

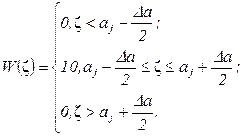
Тоді середня потужність шуму квантування:

;

;

.

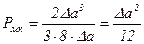Відносну величину потужності шуму квантування визначимо, використавши співвідношення Р_мк до дисперсії випадкового процесу a(t):

.

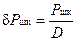Мінімальна кількість двійкових розрядів (k), потрібна для запису в вигляді двійкового числа будь-якого номера з L номерів рівнів квантування, дорівнює:

.

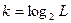Наприклад, представимо j = 29 в двійковій системі (рис. 5. )

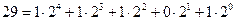
j = 11101

Рис. 5. Часова діаграма відгуку АЦП на рівень j

 

Ентропія H повідомлення (міра невизначеності):

імовірність потрапляння a(t) в інтервал 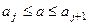 дорівнює:

.

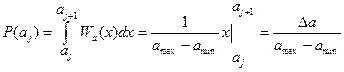При заданому законі розподілу миттєвих значень процесу a(t) усі рівні квантування рівноймовірні, тому що P(a_i) не залежать від i.

Тоді ентропія визначатиметься як ентропія дискретного джерела незалежних повідомлень, усі символи якого рівноймовірні:

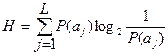 біт/символ.

Продуктивністю такого джерела буде сумарна ентропія повідомлень, переданих за одиницю часу:

.

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: