 |
Демодулятор. Декодер. Цифроаналоговий перетворювач
|
|
|
|
Демодулятор
Демодулятор оптимальний за критерієм максимальної правдоподібності в каналі з адитивною білою гауссівською перешкодою здійснює некогерентне оброблення суміші: z(t)=s(t)+n(t).
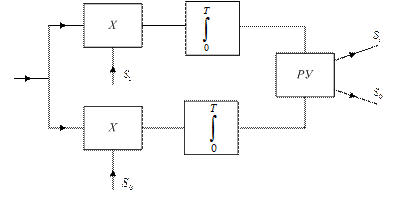Рис. 11. Структурна схема оптимального некогерентного демодулятора
Імовірність помилки оптимального некогерентного демо-дулятора (рис. 11. )для каналу з адитивним білим шумом при передачі двійкових повідомлень визначається так:
.
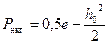Декодер
У декодері процес декодування здійснюється у два етапи. На першому етапі виявляються помилки у кодовій комбінації. Якщо помилок у кодовій комбінації не виявлено, то на другому етапі з неї спочатку виділяються k інформаційних двійкових символів, а потім k-розрядна двійкова кодова комбінація перетворюється в імпульс, висота якого є відповідною квантованому рівню переданого повідомлення.
У разі виявлення помилки в кодовій комбінації виправ-ляється найбільш «ненадійний» символ. Інформація про сту-пінь(міру) надійності символів у кодовій комбінації надходить у кодер з демодулятора.
Визначальна і виправляюча здатності коду визначаються його мінімальною кодовою відстанню dmin за Хеммінгом.
Такий код виявляє всі непарні помилки.
Код гарантовано виявляє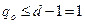 
помилку, а гарантовано виправляє, тобто нічого не виправляє.
Опишемо алгоритм виявлення помилок.
Порозрядно підсумовується слово, що надійшло від демодулятора по модулю 2.
Якщо результат підсумовування n символів кодового слова дорівнює нулю (парна вага помилки), то декодер формує сигнал про відсутність помилки у прийнятому слові немає (хоча цього може і не бути – помилка, що не виявляється) і видає перші к символів на вхід ЦАП.
|
|
|
Якщо результат підсумовування n символів кодового слова ненульовий, це означає, що сталася помилка.
Знайдемо вірогідність не виявлення помилки під час декоду-вання з одною перевіркою на парність за формулою Бернуллі:
Цифроаналоговий перетворювач
У ЦАП з декодера надходить k-розрядне двійкове число – відновлений номер переданого рівня j. Це число перетворюється в короткий імпульс, амплітуда якого відповідає отриманому номеру рівня (відліку). Далі послідовність таких модульованих за амплітудою імпульсів надходить на фільтр-відновлювач, який остаточно виробляє з цієї послідовності відновлене повідомлення a(t).
 |
Запишемо вираз для амплітуди відновленого квантованого відліку aj, який відповідає рівню з прийнятим номером j
Фільтр-відновлювач являє собою фільтр нижніх частот з частотою зрізу Fзр.
За теоремою Котельнікова визначимо частоту зрізу фільтра-відновлювача:
Гц.
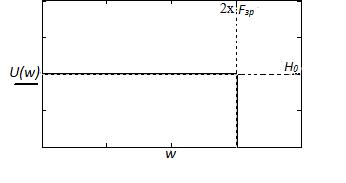
Рис. 12. Ідеальна АЧХ фільтра-відновлювача
Рис. 13. Ідеальна ФЧХ фільтра-відновлювача
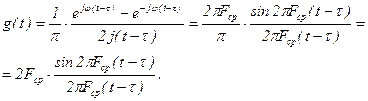
Рис. 14. Імпульсна реакція фільтра-відновлювача
СПИСОК ЛІТЕРАТУРИ
1. Бабак В. П Обробка сигналів у радіоканалах цифрових систем передавання інформації: навч. посібн. / за заг. ред. В. П. Бабака. – К.: Книжкове вид-во НАУ, 2005. – 476 с.
2. Вінницький В. П. Термінальне устаткування та передавання інформації в телекомунікаційних системах. – К. : ІВЦ Видавництво Політехніка, 2004. – 436 с.
3. Игнатов В. А. Теория информации и передачи сигналов: учебник для вузов / В. А. Игнатов– М.: Сов. Радио, 1979. – 280 с.
4. Скляр Б. Цифровая связь. Теоретические основы и практическое применение. / Б. Скляр; пер. с англ., изд. 2-е, испр.: – М.: Издательский дом Вильямс, 2004. – 1104 с.
5. Микроволновые технологии в телекоммуникационных системах / Т. М. Нарытник, В. П. Бабак, М. Е. Ильченко, С. А. Кравчук. – К.: Техніка, 2000. – 304 с.
6. Радиотехнические системы передачи информации: учеб. пособие для вузов / В. А. Борисов, В. В. Калмыков, Я. М. Ковальчук [и др. ]; Под ред. В. В. Калмыкова. – М.: Радио и связь, 1990. – 304 с.
|
|
|
7. Левин А. Л. Цифровые системы передачи информации / А. Л. Левин, М. А. Плоткин – М.: Радио и связь, 1982. – 216 с.
8. Проектирование радиопередающих устройств / Под ред. В. В. Шахгильдяна. – М.: Радио и связь, 1984. – 424 с.
9. Радиопередающие устройства на полупроводниковых приборах / под ред. Р. А. Валитова, И. А. Попова. – М.: Сов. радио, 1977. – 374 с.
10. Радиоприёмные устройства / под ред. А. Жуковского. – М.: Высш. шк., 1989. – 342 с.
11. Проектирование радиоприёмных устройств / Под общ. ред. А. П. Сиверса. – М.: Сов. радио, 1976. – 448 с.
Навчальне видання
|
|
|
