Кодер. Частотний модулятор. Неперервний канал

Кодер

 

Кодер виконує систематичне кодування з однією перевіркою на парність, утворюючи код (n, k).

Сформулюємо правило кодування з перевіркою на парність.

Визначимо перевірний символ в₆ шляхом складання за модулем 2 усіх к=5 інформаційних символів:

правило складання за модулем 2 має вигляд:

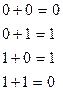
для числа j: в₆ = 1.

Надлишковість коду с однією перевіркою на парність

.

Двійкове кодове слово, утворене в результаті кодування двійкового числа з перевіркою на парність:

 

                     в₁  в₂  в₃   в₄  в₅     в₆

                   1    1   1    0  1    1

                             Інформаційні      Перевірні

                       символи              символи

Рис. 6. Імпульсна послідовність b(t)

 

Кількість двійкових символів, виданих кодером за секунду V_к, визначається кількістю відліків (1/Δ t) і кількістю двійкових символів n=к+1, що припадають на один відлік.

Тривалість двійкового символу як величина зворотна V_k

.

Частотний модулятор

Наведемо вираз функції кореляції B_b(τ ) модульованого сигналу b(t) (рис. 6. ).

Для цього розглянемо два перерізи в моменти t₁ та t₂ (t₂-t₁=τ ) і знайдемо математичні сподівання добутку X(t₁)X(t₁+τ ).

Якщо τ > Т, то ці перерізи належать різним тактовим інтервалам, а добуток може з рівною імовірністю набувати значення +1 і -1, таким чином, доти його математичне сподівання дорівнювало б 0.

Якщо τ < Т, то можливі два випадки: випадок А, коли вони належать одному інтервалу і, отже, X(t₁)X(t₁+τ )=1, і випадок Б, коли вони належать різним тактовим інтервалам та X(t₁)X(t₁+τ ) може з рівною ймовірністю дорівнювати +1 і -1. Тому при τ < Т математичне сподівання X(t₁)X(t₁+τ ) дорівнює ймовірності р(а) того, що обидва перерізи виявляться в одному інтервалі. Випадок А має місце, якщо перший з двох перерізів спізнюється від початку тактового інтервалу не більше ніж Т-|τ |, а ймовірність цього дорівнює (Т - |τ |)/Т.

Тоді функція кореляції має вигляд:

Рис. 7. Функція кореляції

 

Знайдемо вираз для спектральної щільності потужності модульованого сигналу G_b(f) за теоремою Віннера-Хінчіна:

Оскільки В(τ ) - функція парна, то:

;

 

 

Візьмемо інтеграл по частинах:

 

.

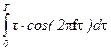
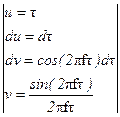
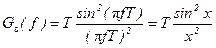Рис. 8. Графік спектральної щільності потужності модулюючого сигналу

 

Обмежимо верхню частоту ширини спектра модулюючого сигналу частотою F_b, при цьому знехтуємо спотвореннями, які виникають у часовій області

 

.    

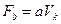Визначимо частину потужності, зосереджену в смузі частот від 0 до :

;

.

 

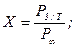
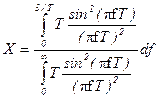Візьмемо цей інтеграл по частинах:

;

; ;

; ;

     ;

.

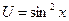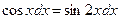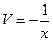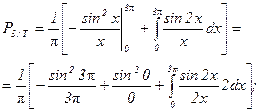
Отримуємо відсоток потужності сигналу який припадає на смугу частот від 0 до F_В.

Задана фазова маніпуляція, тобто

; .

Рис. 9. Часові діаграми залежності сигналу s(t) від сигналу b(t) в разі передавання рівня з номером j.

 

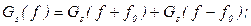При ЧМ вираз енергетичного спектра модульованого сигналу (рис. 10. ) має вигляд:

 

 

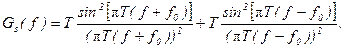
Рис. 10 Графік енергетичного спектра модульованого сигналу G_s(f)

 

Умовна ширина енергетичного спектра буде в два рази більша від умовної ширини енергетичного спектра модулюючого сигналу,

 

Неперервний канал

Передача сигналу s(t) відбувається за неперервним неспотвореним каналом з постійними параметрами і адитивною перешкодою n(t).

Сигнал на виході такого каналу має вигляд:

.

Коефіцієнт передачі каналу

Мінімально допустима смуга частот для каналу: .

Визначимо потужність P_n перешкоди n(t) на виході каналу

.

Передані символи рівноймовірні p(0) = p(1), рівноймовірні і радіоімпульси s₁(t) і s₂(t). У результаті їх середня потужність буде дорівнювати:

,

де Е₀ та Е₁- енергії радіоімпульсів;

Т- тривалість сигналів.

Енергія сигналу визначається як:

.

 Отже,

 

 

 

 

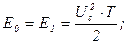
Вт.

Пропускну здатність каналу зв’язку визначимо за теоремою Шеннона, :

.

Визначимо ефективність використання пропускної здатності каналу зв’язку:

 

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: