Построение диаграмм состояния двухкомпонентных конденсированных систем по заданной характеристике компонентов

В основе физико-химического анализа как метода изучения реальных многокомпонентных систем, созданного и блестяще развитого благодаря работам Н.С.Курнакова и его школы, получившего широкое применение во многих областях современной науки и техники, лежат два прин­ципа - принцип непрерывности и принцип соответствия.

Принцип непрерывности Н.С.Курнаков сформулировал следующим образом: «При непрерывном изменении параметров, определяющих состояние системы, свойства отдельных ее фаз изменяются непрерывно; при этом свойства системы, взятой в целом, изменяются тоже непрерывно, но при условии, что не возникают новые фазы и не исчезают наличные». Например, непрерывным изменениям состава жидких или твердых растворов отвечают непрерывные изменения их свойств: плотности, электропроводности, давления пара и других. Появление новой или исчезновение наличной фазы изменяет свойства всей системы в целом, вызывает изломы и остановки на кривой зависимости физического свойства от состава или другого параметра состояния.

Принцип соответствия заключается в следующем: «Каждому комплексу фаз, находящихся в данной системе в равновесии, соответствует на диаграмме состояния определенный геометрический образ». Располагая геометрическим образом, адекватно отражающим определенное сочетание свойств компонентов, т.е. типовыми диаграммами состояния, можно обнаружить эти свойства на диаграмме состояния исследуемой системы. Эта задача решалась при чтении диаграмм состояния. Можно решать и обратную задачу, цель которой заключается в построении диаграммы состояния, геометрия которой адекватно отражает заданную характеристику свойств системы. Решение этой задачи также требует знания типовых диаграмм.

Последовательность действий при построении диаграмм состояния на основании описания диаграммы может быть следующая.

1. Вычислить состав химических соединений постоянного состава, если таковые в системе существуют.

Если состав системы выражен в мольных долях, то для вычисления мольной доли компонента в составе химического соединения следует использовать уравнение:

где n – индексы в формуле химического соединения при химическом элементе. Например, для соединения Fe₂S₃ мольная доля железа

Если состав системы выражен в массовых долях, то для вычисления состава химического соединения следует использовать уравнение массовой доли в расчете на 1 моль вещества:

где и - молярные массы компонентов, г/моль; x и y – стехиометрические индексы при компоненте А и В соответственно. Например, для Fe₂S₃ массовая доля железа

2. Определить и отметить в координатах температура – состав, % В точки, принадлежащие линии ликвидус, и начертить ее.

3. Отметить расположение химических соединений и нанести их на диаграмму.

4. Отметить на диаграмме области существования твердых растворов и нанести линии растворимости.

5. Прочертить линии изотерм (эвтектики, перитектики, полиморфные превращения и др.).

Пример 5. Алюминий (температура плавления 658°С) и кальций (температура плавления 816°С) неограниченно растворимы друг в друге в расплавленном состоянии и образуют два химических соединения: СаА1₂, которое плавится конгруэнтно при 1079°С, а при температуре 549°С находится в равновесии с кальцием и жидкой фазой, содержащей 73 % по массе Са, и СаА1₃, которое разлагается при температуре 700°С на СаА1₂ и жидкость, содержащую 14 % Са. При температуре 616 °С жидкая фаза, содержащая 7,6 % Са, находится в равновесии с кристаллами СаА1₃ и твердой фазой, содержащей примерно 0,7 % Са. При 450 °С кристаллический кальций испытывает полиморфное превращение.

Построить диаграмму состояния системы алюминий - кальций, обозначить поля, показать на изотермах треугольники Таммана.

Определить состав и количество находящихся в равновесии фаз при 600 °С, если проба сплава была приготовлена путем смешения равных по массе навесок алюминия и кальция.

Решение. 1. Вычислить массовую долю кальция в каждом из химических соединений:

;

.

2. Построение диаграммы начать с размещения в масштабе на отрезке оси абсцисс шкалы состава системы, а на оси ординат - шкалы температуры с учетом минимального и максимального ее значений, заданных в условии задачи.

Рис. 42 а. Первый этап построения двухкомпонентной диаграммы состояния по ее описанию.

3. Нанести на диаграмму точки ликвидуса, отвечающие равновесию между твердой и жидкой фазами: ; ; ; ; . Координаты точки эвтектик получены из описания соответствующих равновесий (на диаграмме состояния выглядит как изотерма):

для E ₁ дано описание: «при температуре 616 °Сжидкая фаза, содержащая 7,6 % Са, находится в равновесии с кристаллами СаА1₃ и твердой фазой, содержащей примерно 0,7 % Са», следовательно точка ликвидуса имеет координаты 616°С и 7,6 % Са;

для точки перитектики дано описание: «СаА1₃ …. разлагается при температуре700°С на СаА1₂ и жидкость, содержащую 14 % Са», следовательно, к ликвидусу относится точка с координатами 700°С и 14 % Са;

для второй точки эвтектики дано описание: «при температуре 549°С CaAl₃ находится в равновесии с кальцием и жидкой фазой, содержащей 73 % по массе Са, и СаА1₃», следовательно, к ликвидусу относится точка с координатами 549°С и 73 % Са.

Рис. 42 б. Расположение точек ликвидуса при построении диаграммы состояния.

4. Соединить точки ликвидуса плавными выпуклыми линиями:

Рис. 42 в. Прорисовка ликвидуса.

5. Провести линии составов химических соединений и отметить точку солидуса, отвечающую составу твердого раствора с координатой 616°С - 0,7 % Са. Информация о положении точки солидуса содержится в описании диаграммы: «при температуре 616 °С жидкая фаза, содержащая 7,6 % Са, находится в равновесии с кристаллами СаА1₃ и твердой фазой, содержащей 0,7 % Са»

Рис. 42 г. Обозначены линии химических соединений и точки солидуса.

6. Обозначить линии эвтектик, перитектики и полиморфного превращения кальция горизонтальными линиями:

Рис. 42 д. Размещение линий изотерм.

7. Завершить формирование диаграммы линией, ограничивающей область существования твердого раствора и треугольниками Таммана:

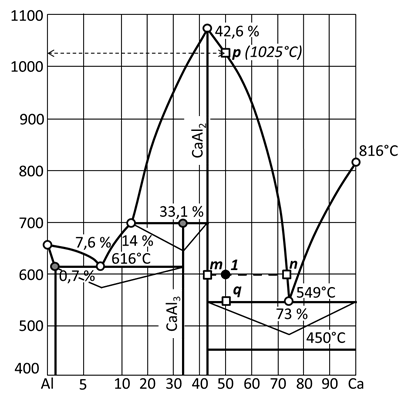
Рис. 42 е. Окончательное оформление диаграммы состояния двухкомпонентной системы.

Вершины треугольников Таммана, построенные на изотермах диаграммы, соответствуют определяющим фазам, от количества которых зависит продолжительность температурных остановок на кривых охлаждения.

Проба сплава, содержащего 50 % по массе кальция и алюминия, при температуре 600°С представлена двумя находящимися в равновесии фазами: жидкой и кристаллами соединения СаАl₂. Состав этих фаз следует определить по ноде (линия m-n), проведенной через точку 1, используя одну степень свободы, которую имеет система в этой точке. Состав жидкой фазы соответствует точке n ликвидуса, содержащей 73 % Са. Твердая фаза (точка m, расположенная на линии состава химического соединения CaAl₂) содержит 43 % Са.

Относительное количество этих фаз вычисляется по правилу рычага, т.е. по длине отрезков ноды, противолежащих фигуративным точкам фаз. Длина ноды пропорциональна общей массе фаз: . За относительное количество жидкой фазы отвечает отрезок [ m 1], длина которого ; за относительное количество твердой фазы отвечает отрезок [1 n ], длина которого .

Следовательно, относительное количество жидкости

от общей массы системы,

а относительное количество твердой фазы (соединения CaAl₂)

.

Кристаллизация жидкой пробы, содержащей 50 % кальция, начинается на ликвидусе (точка p) при температуре 1025 °С и заканчивается на солидусе (точка q) при 545 °С. В пределах этих температур из расплава длительное время (равновесно) кристаллизуется только одна твердая фаза - химическое соединение СаАl₂.

⇐ Предыдущая78910111213141516Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: