Задача 4.1. определить прямоугольные координаты вершин треугольника.

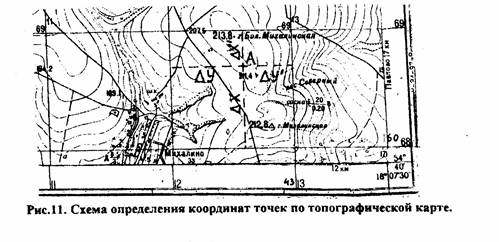
Для решения задачи каждому студенту необходимо иметь ксерокопию карты, на которой преподаватель наносит вершины треугольника АВС. Прежде чем приступить к решению задачи необходимо определить масштаб карты и разобраться с оцифровкой сетки координат. Затем выделить квадрат километровой сетки, в которой находится вершина треугольника и выписать координаты его юго-западного угла. На рис. 11 для точки А Х=6068 км, Y=4312 км (напоминаем, что первая цифра у ординаты означает номер зоны, в которой находится данная карта).

Из точки А опускают перпендикуляры на стороны квадрата километровой сетки. С помощью измерителя и масштабной линейки определяют длины перпендикуляров относительно южной и западной стороны квадрата. То есть измеряют приращения координат. Тогда значения координат точки А будут равны:

XA=Xю.з.+ ∆XA (4)

YA=Yю.з..+ ∆YA (5)

Недостатком изложенного способа является его бесконтрольность. Здесь любая грубая ошибка в измерении остается незамеченной. Поэтому на практике измеряют не только отрезки ∆ХА и ∆YA, но и продолжения их до северной и восточной сторон километровой сетки, т.е., ∆ХА ´ и ∆YA´. Очевидно, что при отсутствии погрешности в измерениях должны выполнятся условия

∆XA +∆ХА´=D (6)

∆YA+∆YA´=D (7)

где D – длина стороны квадрата километровой сетки.

Практически таких равенств не получается из-за случайных и систематических погрешностей измерений (деформация бумаги, не точность установки игл измерителей в вершины, погрешности построения поперечного масштаба и т.д.). Однако величина неравенства не должна превышать 0.3 мм в масштабе карты. Если это условие выполняется, то окончательные координаты точки А можно вычислить по формулам.

 

XA=Xю.з+(D/(∆XA +∆ХА´))∆XA, (8)

 

YA=Yю.з+(D/(∆YA +∆YB´))∆YA. (9).

Данные формулы и рекомендуется использовать при решении задачи 4.1. результаты измерений записывают в таблицы 2 и 3.

 

 

 

 

В качестве примера в этих таблицах приведены результаты измерения координат вершин треугольника АВС (см. Приложение 1)

Абсциссы точек А, В,С. (км) Таблица2.

Точка	Xю.з	∆X	∆Х´	Х
А		0.356		6068.356
В		0.582	0.413	6067.585
С		0.451	0.545	6067.453

Ординаты точек А,В,С (км) Таблица 3.

Точка	Yю.з	∆Y	∆Y´	Y
А		0.296	0.702	4311.297
В		0.193		4312.193
С		0.151	0.847	4311.151

 

Задача 4.2. По измеренным в задаче 4.1 прямоугольным координатам вычислить длины сторон треугольника и сравнить их с непосредственно измеренными.

Задача распадается на 2 части. В первой части необходимо вычислить длины сторон по известной в математике формуле

dAB=√(XA-XB)²+(YA-YB)². (10)

вычисленные расстояния записать в таблицу 4 с числом значащих цифр, б

соответствующих точности масштаба карты.

Вторая часть задачи состоит в непосредственном измерении длин сторон треугольника с помощью измерителя и построенного поперечного масштаба.

Результаты измерений также записать в таблицу 4. Найти расхождения между вычисленными и измеренными длинами сторон треугольника и дать анализ их

соответствия точности масштаба карты. Перечислить причины возникновения этих расхождений.

Значения длин сторон треугольника, полученные при вычислениях и измерениях.

 

Названия сторон	Приращения ∆X	координат ∆Y	Длины Вычисленные	сторон Измеренные	Расхождения (м)
AB	-0.771	0.896			-1
BC	-0.132	-1.042
AC	0.903	0.146			-5

Вопросы для самоконтроля.

1. В чем сущность зональной системы прямоугольных координат?
2. Что принято за ось ординат и абсцисс в зональной системе координат?
3. В чем смысл преобразования ординаты?
4. Как определить номер зоны данного листа карты?
5. Какие погрешности влияют на точность измерения координат (длин линий) по карте?
6. Как определить длину отрезка, зная прямоугольные координаты его концов?
7. Чему равны искажения длин линий на осевом меридиане?
8. Как вычислить искажения длин линий в пределах зоны?
9. Как построить на карте точку по известным прямоугольным координатам?
10. Чем вызваны искажения картографических проекций?
11. Какие искажения присущи проекции Гаусса-Крюгера?

 

1. Ориентирование.

Ориентировать линию или карту – значит определить ее расположение относительно географического (истинного), осевого или магнитного меридианов.

 

Угол ориентирования, отсчитываемый от северного направления географического меридиана, называется истинным азимутом.

Трудность такого ориентирования связана с изменением величины азимута от протяженности длины линии и широты точки, в которой он измеряется. Данное обстоятельство вызвано тем, что меридианы не параллельны друг другу.

Угол между проекциями смежных меридианов на плоскости называется сближением меридианов и обозначается буквой γ и вычисляется по формуле

γ=(LA-LM) sin B, (11),

где LA и LM – долготы меридианов, проходящих через точки А и М, В – широта точки А.

Поэтомупри измерении истинного азимута линии АМ не безразлично в какой точке (А или М) производится измерение угла. Так как значения сближения меридианов изменяется, то и азимут ААМ ≠АВА+180 °. Однако, при измерении азимутов по крупномасштабным картам задача упрощается. Это связано с низкой точностью измерения углов транспортиром и малой протяженностью линии. Действительно, даже геодезическим транспортиром точность измерения угла не превышает ±15΄. А если учесть, что протяженность линии на карте масштаба 1:50 000по долготе не превышает 15΄, то для средних широт (В=55°) по формуле (11) получим γ≈12´. То есть сближение крайних меридианов карты не больше 12´, а это как видим, меньше точности измерения углов транспортиром. Для карт более крупного масштаба величина сближения меридианов в пределах данной карты будет еще меньше, а следовательно, ее можно не учитывать при измерении истинных азимутов по карте. Это позволяет производить их измерение в любой точке линии.

Задача 5.1. Измерить с помощью транспортира азимуты линий АВ, ВС, СА, ВА, СВ, АС. Вычислить румбы и внутренние углы треугольника АВС.

Для измерения азимута линии АВ необходимо провести географический меридиан, пересекающий сторону АВ треугольника (приложение 1) или продолжить сторону АВ до пересечения с меридианом, ограничивающим лист карты с запада или востока. От северного направления этого меридиана по ходу часовой стрелки транспортиром измерить искомый угол ориентирования. Результат измерения занести в таблицу 5. Точно также измерить азимуты остальных сторон. От азимутов перейти к румбам и вычислить величины внутренних углов треугольника, используя правило: угол равен разности правого и левого направлений.

Если измерения не содержат грубых погрешностей, то расхождения между значениями прямых и обратных азимутов должно быть точно 180°. Сумма внутренних углов треугольника также должна быть равна 180°. Отклонения от этих величин не должны превышать тройной точности транспортира. В качестве примера в таблице 5 приведены значения азимутов сторон треугольника АВС (приложение 1)

 

 

Таблица 5

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: