 |
Графическое решение векторных уравнений
|
|
|
|
Рассмотренные выше векторные уравнения могут быть решены аналитически или графически. В инженерных расчетах более наглядными и простыми являются графические решения векторных уравнений.  Графическое решение векторных уравнений сводится к построению планов скоростей точек механизма, определению их модулей и расчету угловых скоростей звеньев.
Графическое решение векторных уравнений сводится к построению планов скоростей точек механизма, определению их модулей и расчету угловых скоростей звеньев.
Планы скоростей шатуна шарнирного четырехзвенника
Рассмотрим уравнение

Если известна скорость vB полюса В и направление относительной скорости νсв (рис. 6), то для определения скорости vc нужно знать ее направление. Это и будет линия действия скорости νсв. Вектор скорости vc будет замыкающим двух векторов νв и νсв, поэтому он должен выходить из полюса V. Проводим из полюса V линию Vc || (у - у) до пересечения с линией bc в точке с. В результате получим векторный треугольник Vbc, который соответствует векторному уравнению. Стрелку скорости vB ставим к точке b. Стрелку скорости νсв направляем к точке c, т.к. происходит сложение векторов νв и νсв. Стрелку скорости vC направляем к точке С, т.к. вектор vc является замыкающим, т.е. геометрической суммой векторов νв и νсв.
Длина каждого вектора в миллиметрах на плане скоростей выражает его модуль. Определим числовые значения скоростей
v CB = μV · bc
Если вектор νсв перенести в точку С, то шатун 3 будет вращаться против часовой стрелки относительно полюса В. Направляем стрелку вектора ω 3 влево (рис. 9)
Числовое значение угловых скоростей(рад/с.) определяем по формуле
ω 3 = vcb / l3
ω4 = vC / l4
Для определения скорости точки Е шатуна 3, лежащей в его средине, нужно вектор ее на плане скоростей разделить тоже пополам и его середину е соединить с полюсом. Вектор Ve = vE, а его числовое значение
|
|
|
vE = μV ·Ve

Рисунок 9
Рассмотрим графическое решение векторного уравнения.
На рис. 9 изображено звено 3 (ВС), а тонкими линиями звенья 2 (АВ) и 4 (CD). Точку В выбираем в качестве полюса, т.к. о ней мы имеем полную информацию: задана угловая скорость звена 2 -ω2 и радиус кривошипа АВ, равный r2. По формуле определяем скорость νсв. Проводим из точки В вектор скорости νв 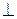 АВ. Через точку С проводим пунктирную линию (х - x)
АВ. Через точку С проводим пунктирную линию (х - x) 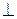 BC, соответствующую направлению скорости νсв, и (у - y)
BC, соответствующую направлению скорости νсв, и (у - y) 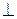 CD, соответствующую направлению скорости vC.
CD, соответствующую направлению скорости vC.
План скоростей – это векторный многоугольник скоростей. Вначале анализируется исходное уравнение:

У вектора νв известны модуль и направление (подчёркнут двумя чертами), у вектора νсв известно только направление (подчёркнут одной чертой). У вектора vc известно тоже только направление.
Построение плана скоростей начнем с выбора длины вектора скорости νв и масштабного коэффициента скорости μV. Если νв=3,3 м/с, а длина вектора νв = 70 мм, то
μV= v B (м/с) / vB (мм) = 3,3 / 70 = 0,047  0,05 (м/с)/мм.
0,05 (м/с)/мм.
Так как масштабный коэффициент округлили, то необходимо уточнить длину отрезка вектора скорости.
На плане скоростей (рис.9) выбираем произвольно положение полюса V и из него перпендикулярно АВ откладываем вектор vB Получаем точку в в конце вектора. Согласно векторному уравнению к вектору vB пристраиваем вектор vCB, о котором знаем только направление. Для этого через точку в проводим линию вс || (х - х) в обе стороны от точки в. Вектор скорости будет замыкающим этих двух векторов и выходить из полюса.
Из полюса перпендикулярно СД проводим линию до пересечения ее с линией вс в точке с. В результате получим векторный треугольник. Длина каждого вектора в миллиметрах на плане скоростей выражает его модуль. Числовые значения скоростей
|
|
|
vcb= μV •вс
vc= μV •Vс
Для определения направления угловой скорости звена 3 необходимо перенести вектор vcb в точку С. Его направление и покажет направление угловой скорости звена.
Числовые значения угловых скоростей определяются по формулам:
ω 3 = vcb / l3
ω4 = vC / l4
Для определения скорости точки Е, лежащей в середине шатуна, нужно в соответствии с теоремой подобия вектор ВС на плане скоростей также разделить пополам и его середину е соединить с полюсом.
Теорема подобия для планов скоростей звеньев:
Отрезки прямых линий, соединяющие точки одного и того же звена на планах механизма, и отрезки прямых линий, соединяющих концы векторов скоростей этих точек на планах скоростей, образуют подобные и сходственно расположенные фигуры.
Планы скоростей кулисного камня
Рассмотрим уравнение:

Полюсом является точка В (рис. 7и 10),принадлежащая камню 3. Требуется определить скорость точки В4. Известны угловая скорость  кривошипа 2 и все геометрические размеры механизма. Скорость точки В определяется по формуле
кривошипа 2 и все геометрические размеры механизма. Скорость точки В определяется по формуле
 .
.
Направлен вектор скорости  перпендикулярно к АВ в сторону вращения кривошипа 2.
перпендикулярно к АВ в сторону вращения кривошипа 2.
Модуль относительной скорости 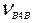 неизвестен, а направлена она вдоль направляющей кулисы х – х
неизвестен, а направлена она вдоль направляющей кулисы х – х
Модуль искомой скорости  также неизвестен, а направлена она перпендикулярно к оси кулисы х-х вдоль у -у.
также неизвестен, а направлена она перпендикулярно к оси кулисы х-х вдоль у -у.
Таким образом, в векторном уравнении неизвестны два модуля 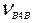 и
и  . Векторное уравнение с двумя неизвестными решается графически.
. Векторное уравнение с двумя неизвестными решается графически.
(у -у) ║  ║ (х - х).
║ (х - х).
Две черточки обозначают, что известен модуль и направление вектора. Одна черточка- известно только направление вектора х-х или у - у. Построение плана скоростей начнем с выбора масштабного коэффициента  и длины вектора
и длины вектора  .
.
 =
=  (м/с) /
(м/с) /  (мм) (м/с) / мм.
(мм) (м/с) / мм.
Длина отрезка на чертеже обычно берется в пределах 50….70 мм. После уточнения длины вектора скорости
Vв =  /
/ 
выбираем положение полюса V, из него откладываем вектор  перпендикулярно АВ. Получаем точку В в конце вектора.
перпендикулярно АВ. Получаем точку В в конце вектора.
Согласно векторному уравнению к вектору  пристраиваем линию действия вектора
пристраиваем линию действия вектора 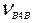 . Вектор
. Вектор  есть замыкающий векторов
есть замыкающий векторов  и
и 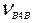 , поэтому из полюса V проводим линию действия вектора
, поэтому из полюса V проводим линию действия вектора 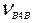 параллельную (у- y) до пересечения с х - х в точке В4. В результате получаем векторный треугольник Vвв4, который соответствует векторному уравнению Стрелки скоростей
параллельную (у- y) до пересечения с х - х в точке В4. В результате получаем векторный треугольник Vвв4, который соответствует векторному уравнению Стрелки скоростей 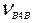 и
и  направляем к точке в4.
направляем к точке в4.
|
|
|

Рисунок 10
Построение плана скоростей начнем с выбора длины вектора скорости vB и масштабного коэффициента скорости μV. Если νв=4,8 м/с, а длина вектора v B = 70 мм, то
μV= v B (м/с) / vB (мм) = 4,8 / 70 = 0,0686  0,07 (м/с)/мм.
0,07 (м/с)/мм.
Окончательно после округления масштабного коэффициента длина вектора скорости
Vв =vB /μV = 68,5 мм.
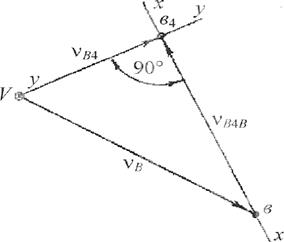
Рисунок 11
На плане скоростей (рис.11) выбираем положение полюса V, из него откладываем вектор  , направленный перпендикулярно АВ. Согласно векторному уравнению к вектору
, направленный перпендикулярно АВ. Согласно векторному уравнению к вектору  пристраиваем линию действия вектора
пристраиваем линию действия вектора 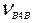 . Вектор
. Вектор  есть замыкающий векторов
есть замыкающий векторов  и
и 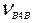 , поэтому из полюса V проводим линию действия вектора
, поэтому из полюса V проводим линию действия вектора  (y - y) до пересечения с х - х в точке в4. В результате получаем векторный треугольник Vвв4, который соответствует векторному уравнению Стрелки скоростей
(y - y) до пересечения с х - х в точке в4. В результате получаем векторный треугольник Vвв4, который соответствует векторному уравнению Стрелки скоростей 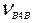 и
и  направляем к точке в4.
направляем к точке в4.
Длина каждого вектора на плане скоростей (мм) выражает его модуль. Предположим, что отрезки вв4 и Vв4, снятые с планов скоростей составляют 55 и 38 мм. Определим числовые значения скоростей:
 м/с;
м/с;
 м /с.
м /с.
Если вектор  перенести в точку
перенести в точку  (рис. 10), то он покажет, что кулиса 4 вращается по часовой стрелке, а числовое значение угловой скорости, рад/с
(рис. 10), то он покажет, что кулиса 4 вращается по часовой стрелке, а числовое значение угловой скорости, рад/с
 ;
;
 ,
,
где  ,м;
,м;  , м.
, м.
Планы скоростей камня синусного механизма
Синусный механизм отличается от кулисного тем, что кулиса 4 совершает поступательное движение (рис.7, б).
Векторное уравнение скорости соответствует уравнению

 ,
,
где  ║ (у - у) - абсолютная скорость точки В4 (т.е. кулисы), которая равна по величине и направлению скорости
║ (у - у) - абсолютная скорость точки В4 (т.е. кулисы), которая равна по величине и направлению скорости  ползуна 4 (рис.7,б);
ползуна 4 (рис.7,б); 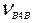 ║ (х -х) - относительная скорость, как и в кулисном механизме.
║ (х -х) - относительная скорость, как и в кулисном механизме.
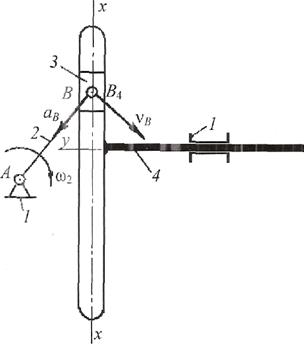
Рисунок 12
Известны величина и направление вектора  , а также направление векторов
, а также направление векторов  и
и 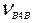 . В результате анализа получаем векторное уравнение с двумя неизвестными
. В результате анализа получаем векторное уравнение с двумя неизвестными
|
|
|
(у - у) ║  ║(х-х).
║(х-х).
Построение плана скоростей аналогично кулисному механизму (рис.13), но в плане скоростей направление (х - х) всегда вертикально, а направление (у - у) везде горизонтально (рис.13).
Определим числовые значения скоростей:
 .
.
 .
.
В синусном механизме вращается только кривошип 2, а кулиса, ползун 4 и кулисный камень 3 движутся поступательно.
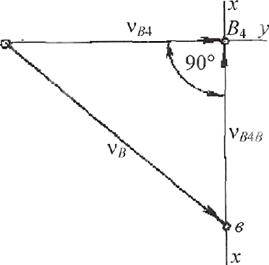
Рисунок 13
Планы скоростей кривошипно-ползунного механизма
Рассмотрим уравнение:
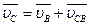 ,
,
где  ║ (х - х) - скорость абсолютная точки С (т.е. ползуна 4, см. рис. 13);
║ (х - х) - скорость абсолютная точки С (т.е. ползуна 4, см. рис. 13); 
 ВС - относительная скорость как в шарнирном четырехзвенном механизме (см. рис.9).
ВС - относительная скорость как в шарнирном четырехзвенном механизме (см. рис.9).
Таким образом, в векторном уравнении (рис 12) два неизвестных модуля  и
и  .Такое уравнение решается графически
.Такое уравнение решается графически
(х - х)║ 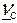 =
=  +
+ 
 ВС.
ВС.
Выбираем на плане скоростей полюс V и откладываем вектор  . Из точки в, плана скоростей проводим линию действия относительной скорости
. Из точки в, плана скоростей проводим линию действия относительной скорости 
 СВ. Из полюса V проводим линию действия вектора
СВ. Из полюса V проводим линию действия вектора  ║(х -х) до пересечения в точке с. Полученный векторный треугольник
║(х -х) до пересечения в точке с. Полученный векторный треугольник  соответствует векторному уравнению.
соответствует векторному уравнению.

Рисунок 14
Числовые значения скоростей определим по формуле
 , м/с;
, м/с;
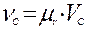 , м/с.
, м/с.
Определить числовые значения угловых скоростей:
 , рад/с;
, рад/с;
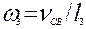 , рад/с.
, рад/с.
4 Варианты схем механизмов
для лабораторной работы
Варианты схем механизмов приведены в Приложении А. Эти варианты общие для данной лабораторной работы и лабораторной работы «Построение планов положений механизмов»
|
|
|


