Порядок проведения XYZ-анализа следующий.

1. Формулирование цели анализа.

2. Определение коэффициентов вариации по отдельным позициям анализируемого множества.

3. Группировка объектов множества в порядке возрастания ко­эффициента вариации

4. Построение кривой XYZ.

5. Разделение множества анализируемых объектов на три группы – группа X, группа У и группа Z.

Предлагается разделять ассортимент товаров на группы в соответствии с тем, в какой интервал попадает коэффициент вариации на данной позиции. Для данной задачи предлагаются следующие диапазоны групп (см. табл. 9).

 

Таблица 9

Границы интервалов

для разделения ассортимента по группам

Группа	Интервал, %
X	0 ≤ υ ≤ 10
Y	10 ≤ υ ≤ 25
Z	25 ≤ υ ≤ ∞

 

В общем случае выбор алгоритма распределения рекомендуетcя осуществлять исходя из того, что указанные границы интервала могут не отражать специфики конкретного множества. Поэтому, так же как и для АВС-анализа, предлагается построить кри­вую, а затем определять разделение на группы, руководствуясь участками кривой, между которыми происходит резкое изменение радиуса ее кривизны.

В решаемой задаче цель XYZ-анализа – распределение позиций ассортимента по группам в зависимости от степени неравно­мерности спроса по каждой ассортиментной позиции. То есть необ­ходимо определить:

- позиции ассортимента, объемы реализации по которым прак­тически неизменны во времени (группа X);

- позиции ассортимента, объемы реализации по которым меняются во времени, но не очень значительно и/или достаточно предсказуемо (группа У);

- позиции ассортимента, объемы реализации по которым ме­няются во времени значительно и практически непредсказуемо (группа Z).

Исходя из этого, объект анализа – данные по реализации то­варных запасов (в денежном выражении) по ассортиментным по­зициям, а признак анализа – степень неравномерности реализа­ции ассортиментных позиций с течением времени.

Следовательно, для проведения анализа рассчитаем коэффицие­нт вариации для каждой позиции ассортимента (графа 3 табл. 15). Коэффициент вариации рассчитывается по формуле (4).

Затем выстроим ассортиментные позиции в порядке возрастания значения коэффициента вариации. Упорядоченный список размещен в графе 4 – 7 табл. 10

Таблица 10

Расчеты и результат анализа XZY

Исходные данные	Коэффициент вариации %	Упорядочный список	группа
№	Реализация за:
квартал	2 квартал	3 квартал	4 квартал	Коэффициент вариации %	№ Позиции
					6,4	1,7		Группа X
					21,2	2,6
					48,3	2,9
					5,8	№.5
					69,8	3,6
					11,8	4,3
					20,8	4,3
					2,6	4,7
					41,4	5,1
					3,6	5,8
					1,7	6,1
					2,9	6,4
					6,1	7,1
					23,4	7,9
					17,7	10,4
					22,6	11,0		Группа Y
					24,5	11,8
					59,1	12,1
					43,1	14,4
					64,9	14,7
					14,4	15,1
					4,3	15,3
					113,2	17,5
					24,7	17,7
					11,0	17,7
					17,7	20,8
					4,3	21,2
					70,7	21,6
					28,3	22,6
					24,3	23,4
					35,4	24,3
					78,2	24,5
					26,4	24,7
					7,9	28,3		Группа Z
					50,7	33,3
					53,6	35,4
					5,1	41,4
					15,3	43,1
					3,5	48,3
					24,8	50,2
					7,1	53,6
					14,7	59,1
					17,5	64,9
					12,1	69,8
					27,3	70,7
					15,1	78,2
					10,4	113,2

 

По итогам анализа АВС и анализа XYZ строится матрица АВС – XYZ (табл. 11), после чего выделяются товарные позиции, требующие наиболее тщательного контроля.

Таблица 11

Матрица ABC – XYZ

	X	Y	Z
A	27, 8, 34, 40, 11, 10	49, 25
B	1, 12, 42, 13, 4, 22	47, 6, 43, 50, 30, 46, 2, 45
C	44, 37	35, 14, 41, 15, 16, 21, 7, 17, 24, 26	33, 9, 29, 39, 32, 48, 36, 28

Для товарных позиций, входящих в группы АХ, АУ, АZ, следует выработать и применять индивидуальные технологии управления запасами, поскольку, согласно классификации АВС, большая по численности группа А связывает в запасах значительную часть (80%) финансовых средств. Например, для позиций, входящих в группу АХ, необходимо рассчитать оптимальный размер заказа и рассмотреть возможность применения технологии «в срок», объем реализации по этим позициям относителен во времени. Позиции же, входящие в группу АZ, необходимо контролировать ежедневно. В связи с большими колебаниями запаса необходимо предусмотреть достаточный для их сглаживания страховой запас.

Планирование запасов по позициям, входящим в группы CZ, может осуществляться на более длительный период (например, на квартал) с еженедельной или ежемесячной проверкой наличия запаса на складе. Это обусловлено тем, что данные запасы «замораживают» сравнительно небольшую часть денежных средств, а колебания спроса на эти позиции значительны.

Достаточно сложным вопросом является управление запасами по позициям, входящим в группы ВХ, ВУ, ВZ. Запасы по этим позициям составляют небольшую, но значимую группу. Относительно колебаний спроса также сложно сделать какие-либо определенные выводы. Вообще, управление запасами по этим позициям может осуществляться как по одинаковым, так и по индивидуальным технологиям планирования.

Варианты для самостоятельного решения

Приведены в приложении 5.

Транспортная логистика

Методические указания к проведению деловой игры

По организации материально-технического снабжения и рациональному использованию материальных ресурсов.

Задача 24.

Определение потребности в бензине для парка грузовых автомобилей в условиях лимитирования горюче-смазочных материалов.

Характеристика игры

В игре моделируется деятельность плановой группы отдела материально-технического снабжения (ОМТС) предприятия, име­ющего собственный парк грузовых автомобилей, например, авто­транспортного предприятия. Выполняя расчеты потребности в бен­зине, плановая группа ОМТС должна увязать эту потребность с производственным планом, т. е. с запланированным объемом перевозок. При этом расчетная потребность не должна превышать установленный для предприятия лимит расхода бензина. Суть конфликта – обеспечить выполнение плана и не превысить ус­тановленный лимит.

Ограничение материальных и топливно-энергетических ре­сурсов при увеличении объема работ выражает требования ин­тенсификации производства и ресурсосбережения. Эти требова­ния могут быть представлены в виде заданий по среднему сни­жению норм расхода материалов или в виде уменьшения выде­ляемых ресурсов, или (как в настоящей игре) прямым лимити­рованием, т. е. в виде установленного лимита. Такое положение усложняет работу отделов материально-технического снабжения и (по мнению некоторых работников снабжения) ставит их в безвыходное положение. Однако решение поставленной задачи возможно, как правило, силами самого предприятия.

Определение потребности в бензине допускает несколько вариантов плановых расчетов. Эти варианты отличаются друг от друга сложностью, объемом вычислительных работ, а сле­довательно, получаемым результатом. Выбор того или иного метода расчета потребности обусловлен традициями данного пред­приятия, его отношениями с вышестоящими организациями, действующей системой экономического стимулирования, ква­лификацией работников, уровнем использования ЭВМ. Так, потребность в бензине может определяться:

- от достигнутого уровня отчетного периода;

- от списочного числа автомобилей;

- от общей длины пробега автомобилей;

- от объема транспортной работы;

- от объема перевозимого груза.

Перечисленные методы определения потребности в бензине в данном случае являются правилами игры.

В игре может участвовать до 7 групп (по 3-4 чел. в каждой), представляющих отдел материально-технического снабжения. Ру­ководитель игры (преподаватель) представляет другую сторону, т. е. сторону, установившую лимит расхода бензина. Целесообразно придать игре соревновательный характер: выигравшей становится та группа, которая найдет наилучшее решение. Игра проводится с использованием микрокалькуляторов или ЭВМ.

Содержание игры

Цель игры. Определить потребность в бензине для парка грузо­вых автомобилей в условиях лимитирования горюче-смазочных материалов. Условия достижения цели игры:

М ≤ L,

где М – расчетная потребность в бензине;

L – установленный лимит.

Указание руководителю игры. Достижение цели игры возмож­но только при оптимизации маршрутов перевозки грузов, но к этому выводу должны прийти сами участники игры и соответ­ствующим образом выбрать метод расчета потребности в бензи­не. Оптимизация маршрутов и выражает рациональную органи­зацию транспортного процесса

Методические указания для участников игры

Методы определения потребности в бензине подразделяются в зависимости от ряда факторов.

1. В зависимости от числа грузовых автомобилей:

М= H_{N *} N,

где Н _{N –} норма расхода бензина в расчете на один автомобиль

в год, т;

N – списочное число грузовых автомобилей.

2. В зависимости от уровня расхода бензина в отчетном году:

М = М_О * К₁* ' К₂

где М₍₎ – расход бензина в отчетном году, т;

К 1 – коэффициент изменения объема транспортной работы в планируемом (оду;

К2 – коэффициент снижения нормы расхода.

3. В зависимости от общего пробега парка грузовых автомобилей

М=Н 1* ∑I,

где Н1 – норма расхода бензина в расчете на 100 км пробега, л;

∑I – общий пробег парка автомобилей, км.

4. В зависимости от объема перевозимого груза:

М = Н _Q * Q,

где Н _Q – норма расхода бензина в расчете на I т перевозимого груза на весь планируемый период, т;

Q – объем перевозимого груза, тыс. т.

5. В зависимости от объема транспортной работы:

М = Н w *W

где Н w – групповая норма расхода бензина, г/т6 км;

W – общий объем транспортной работы, тыс. км.

Групповая норма расхода бензина определяется на основе ли­нейных (индивидуальных) норм расхода по следующей форму­ле:

Hw = 10 у (Н/ q.z)

где Н, – средневзвешенная норма расхода бензина на пробег, л/100 км; определяется исходя из линейных (индивидуальных) норм расхода;

q – средневзвешенная грузоподъемность автомобилей;

z – коэффициент полезной работы автомобилей;

у – плотность бензина, у = 0,74 г/л.

Исходные данные игры

Автотранспортное предприятие согласно договору осуществляет перевозки с трех баз снабжения 24 предприятиям-потребите­ лям.

1. Ресурсы баз.

База NQ 1 – 220 тыс. т; База NQ 2 – 380 тыс. т;

База NQ 3 – 400 тыс. Т

Таблица 12

Потребность предприятий-потребителей, тыс. т

№ Предприятия
Потребность
№ Предприятия
Потребность
№ Предприятия
Потребность

 

Таблица 13

Расстояние между базами и предприятиями, км

№ предприятия	№ базы	№ предприятия	№ базы
			17,

 

Таблица 14

Показатели работы автотранспортного предприятия

№ п/п	Показатели	Обозна- чение	Единица измерения	Значение
	Списочное число
	автомобилей	N	ед.
	Коэффициент полезной
	работы	z		0,5
	Объем перевозок (план)	Q	тыс. т	1 000
	Объем транспортной работы:	w
	а) отчет;		тыс. т.км	16 781
	б) план на следующий год		тыс. T'Kf'1I	17 300
	Общий пробег (отчет)	I./	тыс. км	7 425
	Израсходовано бензина
	(отчет)	Мо	т	1 929,3
	Задание по снижению
	нормы расхода бензина		%	5,0
	Нормы расхода бензина:
	а) на автомобиль
	(годовая);	HN	т	5,64
	б) на перевозимый груз	Но	л/т	1,98

 

Таблица 15

Сведения об автопарке

Наименование марок и моделей автомобилей	Списочное число	Грузоподъ- емность, т	Линейная норма расхода, л/100 км
ГАЗ-51		2,5
Урал-355		3,0
ГАЗ-53Ф		3,0
ГАЗ-53А		4,0	29,5
ЗИЛ-130		5,0	36,5
Урал-377		7,5	55,5

 

Методические указания для руководителя игры

Возможны следующие варианты реализации игры, определе­ния потребности в бензине (см. также Методические указания для участников игры).

1. В зависимости от числа грузовых автомобилей:

H_N = 5,64 т; N = 342 ед.;

М = 5,64. 342 = 1928,8 т > L.

2. В зависимости от уровня расхода бензина в отчетном году:

Мо = 1929,3 т; К, = 17 300: 16 781 = 1,03; К2 = 0,95;

М = 1<129,3. 1,03. 0,95 = 1887,8 т > L.

3. В зависимости от общего пробега парка грузовых автомобилей;

а) по отчету:

Н, = 1929,3: 7425 = 26 л/100 км;

М = 26. 7425 = 1929,3 т > L.

б) по нормам (по данным табл. 4.5) определяется

средневзвешенная норма расхода:

Н, = 36,12. 0,74 = 26,7 л/100 км;

М = 26,7. 7425 = 1984,6 т > L.

4. В зависимости от объема перевозимого груза:

Н_Q = 1,98 л/т; Q = 1000 тыс. т;

М = 1,98. 1000 = 1980,0 т > L.

5. В зависимости от объема транспортной работы:

Н = 10 *0,74 = 36,12 / (4,66*0,5) = 114,7 г/т км

Hi = 36,12 л/100 км; q = 4,66 т; z = 0,5; М = 114,7. 17300 = 1984,3 т > L.

Цель игры может быть достигнута при оптимизации маршрутов, т. е. за счет рациональной организации работ. В данном случае следует применить модель транспортной задачи линейного про­граммирования. Используя данные табл. 4.2-4.4, получаем оп­тимальный план перевозки с минимумом транспортной работы 14 361 тыс. т км, отсюда плановая потребность в бензине: М = 114,7 * 14 361 = 1647,2 т < L.

Экономия по сравнению с установленным лимитом составит 74,8 т, или 4,3%

Пример решения транспортной задачи с помощью
MS Excel

Транспортная задача является классической задачей исследования операций. Множество задач распределения ресурсов сводится именно к этой задаче.

В хозяйстве имеются пять складов минеральных удобрений и четыре пункта, куда их необходимо доставить. Потребность каждого пункта в минеральных удобрениях различна, и запасы на каждом складе ограничены. Требуется определить, с какого склада, в какой пункт поставлять, сколько минеральных удобрений для минимизации грузооборота перевозок.

Имеются следующие исходные данные.

Таблица 16

Наличие минеральных удобрений на складах

Склады	Наличие удобрений, т.
Склад №1
Склад №2
Склад №3
Склад №4
Склад №5

 

Таблица 17

Потребность в минеральных удобрениях на различных пунктах

Пункты	Потребность в удобрениях, т.
1 пункт
2 пункт
3 пункт
4 пункт

 

Таблица 18

Расстояния между складами и пунктами доставки

	Пункт 1	Пункт 2	Пункт 3	Пункт 4
Склад №1
Склад №2
Склад №3
Склад №4
Склад №5

 

На пересечении столбца конкретного пункта доставки со строкой склада находится информация о расстояниях между этими пунктом доставки и складом. Например, расстояние между 3 пунктом и складом №3 равно 10 километрам.

Для решения задачи подготовим необходимые таблицы. (рис. 5)

 

Рис.5. Изменяемые ячейки.

 

Значения ячеек по столбцу В с четвертой по восьмую строку определяются суммированием данных ячеек соответствующих строк начиная со столбца С до столбца F.

Например, значение ячейки B4=СУММ(C4:F4)

Значения ячеек по 9 строке по столбцам от С до F определяются суммированием данных ячеек соответствующих столбцов с 4 по 8 строки.

Например, значение ячейки С9=СУММ(C4:C8)

Каждое значение в ячейках на пересечении столбца конкретного пункта доставки и строки склада означает количество тонн, поставляемых с этого склада в данный пункт потребления. В нижней строке (строка 9) суммируется общее количество минеральных удобрений, поставляемых в определенный пункт доставки, а во втором столбце (столбец В) суммируется количество доставленного с конкретного склада минеральных удобрений.

Теперь, используя исходные данные, введем на этом же листе требуемые объемы поставок и расстояния между склдами и пунктами доставки.

Рис.6. Исходная информация.

В строке 16 по столбцам C-F определим грузооборот по каждому пункту доставки. К примеру для 1 пункта (ячейка С16) это рассчитывается с помощью формулы

С16=С4*С11+С5*С12+С6*С13+С7*С14+С8*С15

либо можно использовать функцию СУММПРОИЗВ

С16=СУММПРОИЗВ(C4:C8;C11:C15)

В ячейке С4 находится количество минеральных удобрений, перевозимых со склада №1 в 1 пункт доставки, а в ячейке С11 – расстояние от склада №1 до 1 пункта доставки. Соответственно первое слагаемое в формуле означает полный грузооборот по данному маршруту. Вся же формула вычисляет полный грузооборот перевозок минеральных удобрений в 1 пункт доставки.

В ячейке В16 по формуле =СУММ(С16:F16) будет вычисляться общий объем грузооборота минеральных удобрений.

Таким образом, информация на рабочем листе примет следующий вид (рис. 6)

 

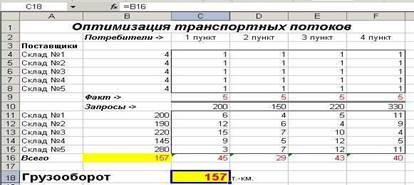
Рис. 7. Рабочий лист, подготовленный для решения транспортной задачи

Для решения транспортной задачи воспользуемся процедурой Поиск решения, которая находится в меню Сервис.

После выбора данной команды появится диалоговое окно (рис. 4).

 

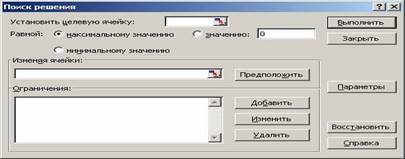
Рис. 8. Диалоговое окно Поиск решения

 

Поскольку в качестве критерия оптимизации нами выбрана минимизация грузооборота, в поле Установить целевую ячейку введите ссылку на ячейку, содержащую формулу расчета общего объема грузооборота минеральных удобрений. В нашем случае это ячейка $B$16. Чтобы минимизировать значение конечной ячейки путем изменения значений влияющих ячеек (влияющими, в данном случае это и изменяемые ячейки, являются ячейки, которые предназначены для хранения значений искомых неизвестных), переключатель установите в положение минимальному значению;

В поле Изменяя ячейки введите ссылки на изменяемые ячейки, разделяя их запятыми; либо, если ячейки находятся рядом, указывая первую и последнюю ячейку, разделяя их двоеточием ($С$4:$F$8). Это означает, что для достижения минимального грузооборота перевозок будут меняться значения в ячейках с С4 по F8, то есть будут изменяться количество груза, перевезенного по конкретному маршруту.

Если сейчас запустить процесс подбора параметров, то будет найден вариант, где все переменные равны нулю. И это правильно – если не перевозить ничего, то это самый дешевый вариант. Но нам необходимо перевезти минеральные удобрения, поэтому надо наложить некоторые ограничения для поиска решения.

В группе полей Ограничения нажмите кнопку Добавить. Появится диалог Добавление ограничения (рис. 8)

 

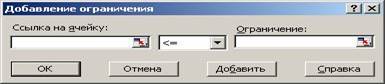
Рис. 8. Диалоговое окно Добавление ограничения

 

Следует ввести левую часть ограничения в левое поле, выбрать знак условия, накладываемого на значение и ввести правую часть ограничения. Как и в других случаях, можно не вводить ссылки на ячейки, а выделить мышью эти ячейки. После ввода одного ограничения следует нажать кнопку Добавить и ввести следующее. По окончании ввода всех ограничений нажмите на кнопку ОК. В диалоге появятся строки введенных ограничений (рис. 9)

 

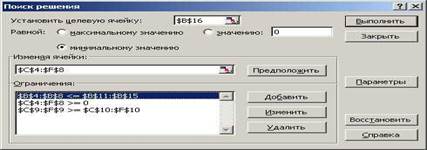
Рис. 9. Диалоговое окно Поиск решения с заполненными полями

 

Для изменения и удаления ограничений в списке Ограничения диалогового окна Поиск решения укажите ограничение, которое требуется изменить или удалить. Выберите команду Изменить и внесите изменения либо нажмите кнопку Удалить.

Рассмотрим более подробно условия, которые следует наложить на значения в некоторых ячейках для правильного решения задачи.

Первое условие $B$4:$B$8 <=$B$11:$B$12. Оно означает, что значение в ячейке В4 должно быть меньше или равно значению в В11, в В5 меньше или равно, чем в В12, и так далее до В8 и В15.

В ячейках с В4 по В8 на листе находятся объемы поставок с конкретных складов. В ячейках с В11 по В15 – запасы на этих же складах. Так как невозможно вывести со склада больше, чем на нем есть, первое значение должно быть не больше второго.

Второе условие $С$4:$F$8>=0. Оно означает, что объем перевозок не может быть отрицательным, то есть, если на складе не хватает минеральных удобрений, их не везут с пункта доставки, на который эти минеральные удобрения были завезены ранее. Грузопоток имеет только одно направление – от складов к пунктам доставки удобрений.

И наконец, третье, и последнее условие $С$9:$F$9>=$C$10:$F$10. Оно означает, что значения в ячейках девятой строки должны быть больше или равны значениям в ячейках десятой строки, то есть запросы пунктов доставки минеральных удобрений должны быть выполнены полностью. Перевыполнение объема поставок допустимо, а недовыполнение – нет.

Введенные условия должны позволить найти наиболее оптимальный вариант решения задачи.. Нажмите кнопку Выполнить для подбора решения.

После нахождения решения появляется диалог Результаты поиска решения (рис. 10)

Рис. 10. Диалоговое окно Результаты поиска решения

Нажав кнопку ОК, вы занесете вариант решения на рабочий лист (рис. 11).

 

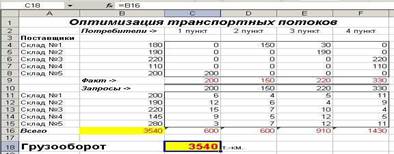
Рис. 11. Решенная транспортная задача

 

Минимальный грузооборот перевозок при соблюдении всех условий равен 3540 т.-км.

 

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: