 |
Корреляционный анализ показателей деятельности песчаных карьеров
|
|
|
|
С.А.Айвазян
В.С.Мхитарян
В.А.Зехин
ПРАКТИКУМ
По многомерным статистическим методам
Москва, 2012
ОГЛАВЛЕНИЕ
Предисловие.......................................................................................................... 4
Глава 1. Корреляционный анализ........................................................................ 5
1.1. Корреляционный анализ показателей деятельности
песчаных карьеров..................................................................................... 5
1.2. Задачи и упражнения......................................................................... 8
1.3. Тест....................................................................................................... 11
Глава 2. Регрессионный анализ (классическая модель).................................... 13
2.1. Регрессионная модель производительности труда......................... 13
2.2. Регрессионная модель урожайности зерновых
культур........................................................................................................ 16
2.3.Задачи и упражнения.......................................................................... 20
2.4. Тест....................................................................................................... 23
Глава 3. Компонентный анализ........................................................................... 25
3.1. Анализ деятельности строительных организаций.......................... 25
3.2. Компонентный анализ деятельности
сельскохозяйственных районов............................................................... 28
3.3. Задачи и упражнения......................................................................... 31
3.4. Тест....................................................................................................... 34
Глава 4. Кластерный и дискриминантный анализ............................................ 36
4.1. Классификация семей по анализируемой структуре
расходов...................................................................................................... 36
4.2. Классификация стран по уровню жизни населения....................... 43
4.3. Классификация мотор-компрессоров бытовых
|
|
|
холодильников по уровню качества........................................................ 45
4.4. Дискриминантный анализ деятельности АО.................................. 48
4.5. Задачи и упражнения........................................................................ 49
4.6. Тест....................................................................................................... 56
Глава 5. Итоговый тест......................................................................................... 58
Литература............................................................................................................. 61
Приложения........................................................................................................... 62
П 1. Варианты заданий для самостоятельных компьютерных
исследований. Исходные статистические данные..................................... 63
П 2. Математико-статистические таблицы.................................................... 65
ПРЕДИСЛОВИЕ
Учебное пособие подготовлено для поддержки практических занятий по дисциплине "Многомерные статистические методы".
Авторы исходили из того, что по указанной дисциплине половина практических занятий проводится в обычных аудиториях, а другая половина - в компьютерных классах. Задачи и упражнения, решаемые в аудиториях, направлены на изучение самих статистических методов и алгоритмов. Цель компьютерных занятий - проведение самостоятельных социально-экономических исследований с использованием статистических пакетов программ для ПЭВМ. Исследования включают в себя постановку задачи, проведение расчетов на ПЭВМ, содержательную интерпретацию полученных результатов и выводы.
В этой связи в учебном пособии алгоритмы рассматриваемых методов прикладной статистики подробно разбираются на экономических примерах, часть из которых решены с помощью микрокалькулятора (ориентированы на аудиторию), а часть - с помощью ПЭВМ. Авторы стремились показать возможности получения многовариантных решений и технику выбора окончательной модели и результата, основываясь не только на статистических приемах, но во многом на априорной (предварительной) информации, которой обычно располагает исследователь в экономике.
|
|
|
Задачи, предлагаемые для самостоятельных исследований достаточно прозрачны в экономическом плане, что дает возможность студенту выступать в роли специалиста, который, проводя компьютерные статистические исследования, всегда в общих чертах представляет, что он может ожидать от ЭВМ при реализации того или иного метода.
Авторы выражают глубокую признательность заведующей лабораторией Прикладной статистики и эконометрического моделирования при кафедре Математической статистики и эконометрики Бамбаевой Н.Я. за помощь в проведении компьютерных расчетов и подготовку оригинал-макета рукописи.
Авторы благодарны преподавателям кафедры: проф. Лукашину Ю.П., доц. Дубровой Т.А., доц. Лукашу Е.Н. за участие в постановке ряда задач, вошедших в Практикум.
Глава 1. Корреляционный анализ
Корреляционный анализ показателей деятельности песчаных карьеров
Деятельность n=8 карьеров характеризуется себестоимостью 1 т. песка (x (3)), сменной добычей песка (x (2)) и фондоотдачей (x (1)). Значения показателей представлены в табл.1.1.
Таблица 1.1.
Показатели деятельности песчаных карьеров
| x (1)(%) | ||||||||
| x (2) (т.) | ||||||||
| x (3) (тыс. руб.) |
Требуется в предположении нормальности распределения трехмерной случайной величины (x (1), x (2), x (3)):
1. Оценить параметры: векторы средних 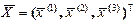 и среднеквадратических отклонений
и среднеквадратических отклонений 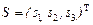 , корреляционную матрицу
, корреляционную матрицу

2. При a=0,05 проверить значимость парного r 13 и частного r 13 (2) коэффициентов корреляции, а при g=0,95 построить их интервальные оценки.
3. Найти точечную оценку множественного коэффициента корреляции 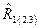 и при a=0,05 проверить его значимость.
и при a=0,05 проверить его значимость.
Решение:
1. Найдем значения средних арифметических  и среднеквадратических отклонений (s k ), где k =1,2,3, а также парных коэффициентов корреляции
и среднеквадратических отклонений (s k ), где k =1,2,3, а также парных коэффициентов корреляции 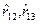 и
и 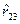 по формулам:
по формулам:
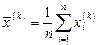 , где i =1,2,...,8; k =1,2,3 (1.1)
, где i =1,2,...,8; k =1,2,3 (1.1)
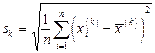 (1.2)
(1.2)
 k,l =1,2,3 (1.3)
k,l =1,2,3 (1.3)
где:
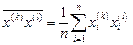
в результате расчетов получим:
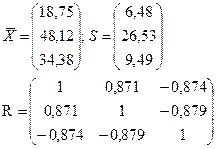
2. Предварительно найдем точечные оценки частных коэффициентов корреляции из выражения
 (1.4)
(1.4)
где R12 — алгебраическое дополнение элемента r 12 корреляционной матрицы R, а R11 и R22 алгебраические дополнения 1-го и 2-го диагонального элемента этой матрицы
|
|
|
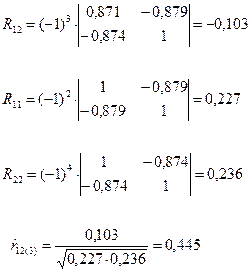
Аналогично находим:  и
и 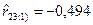 .
.
Для проверки значимости парного r 13 и частного r 13(2) коэффициентов корреляции, т.е. гипотез H0: r13=0 и H0: r 13(2)=0 необходимо по таблице (П.8) Фишера-Иейтса при a=2 Q =0,05 и числе степеней свободы соответственно n=n-2=6 и n=n-2-1=5 определить критические значения 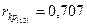 и
и 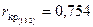 . Так как по абсолютной величине расчетное значение
. Так как по абсолютной величине расчетное значение  , то гипотеза H0: r13=0 отвергается с вероятностью ошибки a=0,05, т.е. r13¹0 и между x (1) и x (3) существует зависимость, отрицательный знак которой экономически объясним. С ростом фондоотдачи себестоимость песка уменьшается.
, то гипотеза H0: r13=0 отвергается с вероятностью ошибки a=0,05, т.е. r13¹0 и между x (1) и x (3) существует зависимость, отрицательный знак которой экономически объясним. С ростом фондоотдачи себестоимость песка уменьшается.
О частном коэффициенте r 13(2) такого однозначного вывода сделать нельзя. Так как 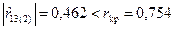 , то гипотеза H0:r13(2)=0 не отвергается, т.е. предположение об отсутствии связи между x (1) и x (3) при фиксированном x (2) не противоречит наблюдениям, хотя их достаточно мало (n =8).
, то гипотеза H0:r13(2)=0 не отвергается, т.е. предположение об отсутствии связи между x (1) и x (3) при фиксированном x (2) не противоречит наблюдениям, хотя их достаточно мало (n =8).
Представляет интерес сравнить парный коэффициент корреляции 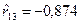 , который характеризует степень тесноты линейной связи между x (1) и x (3) на фоне влияния x (2) и частный
, который характеризует степень тесноты линейной связи между x (1) и x (3) на фоне влияния x (2) и частный  , который характеризует степень тесноты линейной связи между x (1) и x (3), при исключенном влиянии, фиксированной x (2). Так как
, который характеризует степень тесноты линейной связи между x (1) и x (3), при исключенном влиянии, фиксированной x (2). Так как 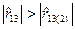 , то можно утверждать, что x (2) усиливает тесноту связи между x (1) и x (
, то можно утверждать, что x (2) усиливает тесноту связи между x (1) и x (
Определим интервальные оценки для коэффициентов корреляции r 13 и r 13(2) при g=0,95. Для этого используем z —преобразование Фишера и предварительно найдем интервальную оценку для z из условия
 (1.5)
(1.5)
где l — порядок частного коэффициента корреляции. Для парного коэффициента корреляции l =0.
По таблице z -преобразования Фишера (П.7) для 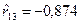 , учитывая что z ¢(‑ r)=‑ z ¢(r), будем иметь z ¢=‑1,350.
, учитывая что z ¢(‑ r)=‑ z ¢(r), будем иметь z ¢=‑1,350.
По таблице нормального закона (П.2) из условия  , найдем t =1,95.
, найдем t =1,95.
Тогда 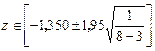
откуда z Î[‑2,222; 0,478].
По таблице z -преобразования (П.7) для z min=‑2,222 и z max=‑0,478 найдем интервальную оценку для r13:
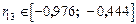 .
.
Полученная интервальная оценка подтверждает вывод о значимости парного коэффициента корреляции r13, т.к. нуль не находится внутри доверительного интервала.
Для частного коэффициента корреляции r 13(2) по таблице z -преобразования (П.7) при r 13(2)=‑0,462 будем иметь 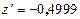 . Тогда
. Тогда
|
|
|
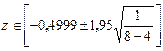
откуда
z Î[‑1,475; 0,475]
По таблице z -преобразования (П.7) для z min=‑1,475 и z max=0,475 найдем интервальную оценку для r 13(2):

Полученная интервальная оценка подтверждает вывод о незначимости частного коэффициента корреляции r 13(2) (нуль находится внутри доверительного интервала).
3. Найдем точечную оценку  и при a=0,05 проверим его значимость. Точечная оценка определяется по формуле
и при a=0,05 проверим его значимость. Точечная оценка определяется по формуле
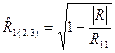 (1.6)
(1.6)
где ½ R ½— определитель корреляционной матрицы.
½ R ½=1+0,871(‑0,879)(‑0,874)+ 0,871(‑0,879)(‑0,874)-(-0,874)2‑0,8712‑(‑0,879)2=0,043
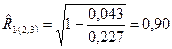
Проверим гипотезу H0: R 1(2,3)=0
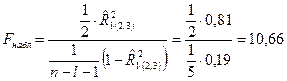 (1.7)
(1.7)
где l =2. Критическое значение по таблице F -распределения (П.5)
F kp(a=0,05, n1=2, n2=5)=5,79
т.к. F набл> F kp, то гипотеза H0 отвергается с вероятностью ошибки a=0,05, т.е. множественный коэффициент корреляции R 1(2,3)¹0, между результирующим показателем x (1) и величинами x (2) и x (3) существует зависимость.
Задачи и упражнения
1.1. Пусть из двумерной генеральной совокупности (x (1), x (2)), имеющей нормальное распределение взята выборка объемом n и пусть(xi (1), xi (2)), где i = 1, 2,..., n, результаты i -го наблюдения. Требуется:
а) доказать тождественность выражений:
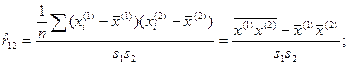 (1.8)
(1.8)
б) доказать справедливость равенств
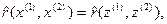
если
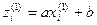 и
и 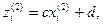
где
a, b, c и d - Const, a ¹ 0 и c ¹ 0.
в) определите при каких соотношениях между xi (1) и xi (2)) коэффициент корреляции 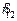 будет равен 1, а при каких -1.
будет равен 1, а при каких -1.
г) доказать, что -1 £ 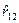 £ 1.
£ 1.
1.2. Пусть из трехмерной совокупности (x (1), x (2), x (3)) имеющей нормальное распределение, взята выборка объемом n, на основании которой получена корреляционная матрица
 .
.
Требуется доказать тождественность выражений для:
а) частного коэффициента корреляции
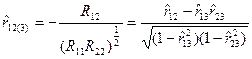 (1.9)
(1.9)
где R12, R11, R22 - алгебраические дополнения соответствующих элементов матрицы R,
б) множественного коэффициента корреляции
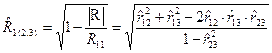 (1.10)
(1.10)
где ½ R ½ - определитель корреляционной матрицы R.
1.3. В табл. 1.2 представлены цены (в руб.) на следующие виды продовольственных товаров: говядина (x (1)), растительное масло (x (2)), сахар-песок (x (3)) и хлеб белый в/с (x (4)) в n =12 городах Центрального района России на июнь 1996г.
Таблица 1.2.
Цены на продовольственные товары в городах
Центрального района России
| i | город | x (1) | x (2) | x (3) | x (4) |
| Брянск | |||||
| Владимир | |||||
| Иваново | |||||
| Калуга | |||||
| Кострома | |||||
| Москва | |||||
| Орел | |||||
| Рязань | |||||
| Смоленск | |||||
| Тверь | |||||
| Тула | |||||
| Ярославль |
|
|
|
Требуется:
а) найти точечную оценку  коэффициента корреляции r 14 между ценами на говядину (x (1)) и хлеб белый в/с (x (4)), при a=0,01 проверить его значимость, а при g=0,875 найти его интервальную оценку. Сравнить полученные результаты;
коэффициента корреляции r 14 между ценами на говядину (x (1)) и хлеб белый в/с (x (4)), при a=0,01 проверить его значимость, а при g=0,875 найти его интервальную оценку. Сравнить полученные результаты;
б) оценить тесноту связи между x (2) и x (3) , при a=0,05 проверить значимость коэффициента корреляции между этими показателями, а при g=0,9 найти интервальную оценку для r 23;
в) определить долю (в %) дисперсии x (4), обусловленную влиянием x (2). При a=0,1 проверить значимость коэффициента корреляции r 24.
1.4. В табл.1.3 представлены темпы прироста (%) следующих макроэкономических показателей десяти развитых стран мира за 1992г.: ВНП (x (1)), промышленного производства (x (2)), индекса цен (x (3)) и доли безработных (x (4)).
Таблица 1.3.
| Страны | x (1) | x (2) | x (3) | x (4) |
| Япония | 3,5 | 4,3 | 2,1 | 2,3 |
| США | 3,1 | 4,6 | 3,9 | 6,3 |
| Германия | 2,2 | 2,0 | 3,4 | 5,1 |
| Франция | 2,7 | 3,1 | 2,9 | 9,7 |
| Италия | 2,7 | 3,0 | 5,6 | 11,1 |
| Великобритания | 1,6 | 1,4 | 4,0 | 9,5 |
| Канада | 3,1 | 3,4 | 3,0 | 10,0 |
| Австралия | 1,8 | 2,6 | 4,0 | 2,6 |
| Бельгия | 2,3 | 2,6 | 3,4 | 8,9 |
| Нидерланды | 2,3 | 2,4 | 3,5 | 6,4 |
Требуется:
а) найти оценку коэффициента корреляции между темпами прироста ВНП (x (1)) и промышленного производства (x (2)), при a=-0,05 проверить его значимость, а при g=0,923 найти его интервальную оценку;
б) оценить тесноту связи между x (1) и x (3), при a=0,05 проверить значимость коэффициента корреляции между этими показателями, а при g=0,857 найти интервальную оценку для r 13;
в) найти точечную и интервальную оценку коэффициента корреляции x (2) по x (3), приняв g=0,95;
г) определить долю дисперсии x (2), обусловленную влиянием x (4);
д) при a=0,05 проверить значимость, а при g=0,888 найти интервальную оценку коэффициента корреляции между x (3) и x (4).
1.5. При исследовании взаимосвязи цен на следующие виды продовольственных товаров: говядина (x (1)), растительное масло (x (2)), сахар-песок (x (3)) и хлеб белый в/с (x (4)) в n =22 городах Центрального района России получена матрица парных коэффициентов корреляции:

Для трехмерной совокупности x (1), x (2) и x (4) требуется:
а) построить матрицу парных коэффициентов корреляции;
б) при a=0,1 проверить значимость частного коэффициента корреляции r 12(4) и найти его интервальную оценку при g=0,954. Сравнить полученные результаты.
Как влияет показатель x (4) на тесноту связи между x (1) и x (2)?
в) при a=0,05 проверить значимость множественного коэффициента корреляции R 4(1,2).
1.6. По данным задачи 1.5 для трехмерной совокупности x (2), x (3), x (4) требуется:
а) построить матрицу парных коэффициентов корреляции R;
б) при a=0,01 проверить значимость частного коэффициента корреляции r 23(4) и найти его интервальную оценку при g=0,9. Сравнить полученные результаты. Как влияет показатель x (4) на тесноту связи между x (3) и x (2)?
в) при a=0,05 проверить значимость множественного коэффициента корреляции R2(3,4). Дайте интерпретацию 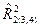 .
.
1.7. При исследовании взаимосвязи темпов приростов (%) следующих макроэкономических показателей десяти развитых стран мира за 1992г.: ВНП (x (1)), промышленного производства (x (2)), индекса цен (x (3)) и доли безработных (x (4)) рассчитана матрица парных коэффициентов корреляции (табл.1.4), а также векторы средних арифметических 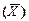 и среднеквадратических отклонений (S):
и среднеквадратических отклонений (S):
 ;
; 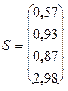 .
.
Таблица 1.4.
| x (1) | x (2) | x (3) | x (4) | |
| x (1) | 1,00 | 0,90 | -0,39 | -0,05 |
| x (2) | 0,90 | 1,00 | -0,28 | -0,23 |
| x (3) | -0,39 | -0,28 | 1,00 | 0,41 |
| x (4) | -0,05 | -0,23 | 0,41 | 1,00 |
Для трехмерной совокупности x (1), x (2) и x (3) требуется:
а) при a=0,05 проверить значимость частного коэффициента корреляции r 12(3) и найти его интервальную оценку с надежностью g=0,925;
б) при a=0,05 проверить значимость множественного коэффициента корреляции R1(2,3).
1.8. По данным задачи 1.7 для трехмерной совокупности x (1), x (2) и x (4) требуется:
а) при a=0,05 проверить значимость частного коэффициента корреляции r 12(4), а также найти его интервальную оценку с надежностью 0,836;
б) при a=0,05 проверить значимость множественного коэффициента детерминации 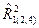 .
.
1.9. По данным задачи 1.7 провести корреляционный анализ трехмерной совокупности x (1), x (3) и x (4), приняв x (1) за результативный признак, и дать экономическую интерпретацию полученным результатам.
1.10. По данным задачи 1.7 провести корреляционный анализ трехмерной генеральной совокупности x (2), x (3) и x (4), приняв x (2) за результативный признак, и дать экономическую интерпретацию полученным результатам.
Тест
1. Известно, что при фиксированном значении x 3 между величинами x 1 и x 2 существует положительная связь. Какое значение может принять частный коэффициент корреляции r 12/3.
а) -0,8; в) 0,4;
б) 0; г) 1,3.
2. По результатам n =20 наблюдений получен частный коэффициент корреляции 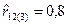 . Определите, чему при уровне значимости a=0,05 равна разность между наблюдаемым
. Определите, чему при уровне значимости a=0,05 равна разность между наблюдаемым 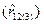 и критическим (r kp) значениями коэффициентов корреляции:
и критическим (r kp) значениями коэффициентов корреляции:
а) -0,513; в) 0,700;
б) 0,344; г) 0,133.
3. Известно, что x 3 усиливает связь между величинами x 1 и x 2. По результатам наблюдений получен частный коэффициент корреляции 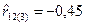 . Какое значение может принять парный коэффициент корреляции
. Какое значение может принять парный коэффициент корреляции 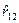 :
:
а) 0,4; в) -0,8;
б) 0,2; г) 1,2.
4. По результатам n =10 наблюдений рассчитан частный коэффициент корреляции 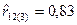 и с доверительной вероятностью g=0,95 найдена интервальная оценка 0,37£ r 12(3)£0,96. Какое значение принимает верхняя граница доверительного интервала для r 12(3) при g=0,9:
и с доверительной вероятностью g=0,95 найдена интервальная оценка 0,37£ r 12(3)£0,96. Какое значение принимает верхняя граница доверительного интервала для r 12(3) при g=0,9:
а) 0,94; в) 0,39;
б) 0,98; г) 0,27.
5. По результатам n =20 наблюдений рассчитан  и найден при g=0,95 доверительный интервал 0,23£ r 13(2)£0,83.
и найден при g=0,95 доверительный интервал 0,23£ r 13(2)£0,83.
Какое значение примет нижняя граница доверительного интервала для r 13(2) при n =10 если g и 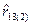 остались неизменными:
остались неизменными:
а) 0,45;
б) 0,20;
в) 0,32;
г) 0,89.
6. Множественный коэффициент корреляции  . Определите, какой процент дисперсии величины x 1 объясняется влиянием x 2 и x 3:
. Определите, какой процент дисперсии величины x 1 объясняется влиянием x 2 и x 3:
а) 28%;
б) 32%;
в) 64%;
г) 80%.
7. По результатам 20 наблюдений найден множественный коэффициент корреляции, т.е. гипотизу  . Проверьте значимость множественного коэффициента корреляции H0:
. Проверьте значимость множественного коэффициента корреляции H0:  при a=0,05 и определите разность между наблюдаемым Fнабл и критическим Fkp значениями статистики критерия:
при a=0,05 и определите разность между наблюдаемым Fнабл и критическим Fkp значениями статистики критерия:
а) 2,8;
б) -13,6;
в) 9,4;
г) 11,5.
8. Какое значение может принимать коэффициент детерминации:
а) -0,5;
б) -0,2;
в) 0,4;
г) 1,2.
9. Какое значение может принять множественный коэффициент корреляции:
а) -1;
б) -0,5;
в) 0;
г) 1,2.
10. По результатам n =25 наблюдений получен парный коэффициент корреляции 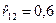 . Известно, что x 3 занижает связь между x 1 и x 2. Какое значение может принять частный коэффициент корреляции:
. Известно, что x 3 занижает связь между x 1 и x 2. Какое значение может принять частный коэффициент корреляции:
а) -0,5;
б) -0,6;
в) 0,5;
г) 0,8.
|
|
|


