Матрица парных коэффициентов корреляций

	y	x (1)	x (2)	x (3)	x (4)	x (5)
y	1.00	0.43	0.37	0.40	0.58	0.33
x (1)	0.43	1.00	0.85	0.98	0.11	0.34
x (2)	0.37	0.85	1.00	0.88	0.03	0.46
x (3)	0.40	0.98	0.88	1.00	0.03	0.28
x (4)	0.58	0.11	0.03	0.03	1.00	0.57
x (5)	0.33	0.34	0.46	0.28	0.57	1.00

Анализ матрицы парных коэффициентов корреляции показывает, что результативный показатель наиболее тесно связан с показателем x ⁽⁴⁾ — количество удобрений, расходуемых на 1 га ().

В то же время связь между признаками-аргументами достаточно тесная. Так, существует практически функциональная связь между числом колесных тракторов (x ⁽¹⁾) и числом орудий поверхностной обработки почвы .

О наличии мультиколлинеарности свидетельствуют также коэффициенты корреляции и . Учитывая тесную взаимосвязь показателей x ⁽¹⁾, x ⁽²⁾ и x ⁽³⁾, в регрессионную модель урожайности может войти лишь один из них.

Чтобы продемонстрировать отрицательное влияние мультиколлинеарности, рассмотрим регрессионную модель урожайности, включив в нее все исходные показатели:

(2.8)

F_набл = 121.

В скобках указаны значения исправленных оценок среднеквадратических отклонений оценок коэффициентов уравнения .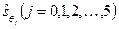

Под уравнением регрессии представлены следующие его параметры адекватности: множественный коэффициент детерминации ; исправленная оценка остаточной дисперсии , средняя относительная ошибка аппроксимации и расчетное значение -критерия F_набл = 121.

Уравнение регрессии значимо, т.к. F_набл = 121 > F_kp = 2,85 найденного по таблице F -распределения при a=0,05; n₁=6 и n₂=14.

Из этого следует, что Q¹0, т.е. и хотя бы один из коэффициентов уравнения q _j (j = 0, 1, 2,..., 5) не равен нулю.

Для проверки гипотезы о значимости отдельных коэффициентов регрессии H0: q_j=0, где j =1,2,3,4,5, сравнивают критическое значение t _kp = 2,14, найденное по таблице t -распределения при уровне значимости a=2 Q =0,05 и числе степеней свободы n=14, с расчетным значением . Из уравнения следует, что статистически значимым является коэффициент регрессии только при x ⁽⁴⁾, так как ½ t ₄½=2,90 > t _kp=2,14.

Не поддаются экономической интерпретации отрицательные знаки коэффициентов регрессии при x ⁽¹⁾ и x ⁽⁵⁾. Из отрицательных значений коэффициентов следует, что повышение насыщенности сельского хозяйства колесными тракторами (x ⁽¹⁾) и средствами оздоровления растений (x ⁽⁵⁾) отрицательно сказывается на урожайности. Таким образом, полученное уравнение регрессии неприемлемо.

Для получения уравнения регрессии со значимыми коэффициентами используем пошаговый алгоритм регрессионного анализа. Первоначально используем пошаговый алгоритм с исключением переменных.

Исключим из модели переменную x ⁽¹⁾, которой соответствует минимальное по абсолютной величине значение ½ t ₁½=0,01. Для оставшихся переменных вновь построим уравнение регрессии:

 

 

Полученное уравнение значимо, т.к. F_набл = 155 > F_kp = 2,90, найденного при уровне значимости a=0,05 и числах степеней свободы n₁=5 и n₂=15 по таблице F -распределения, т.е. вектор q¹0. Однако в уравнении значим только коэффициент регрессии при x ⁽⁴⁾. Расчетные значения ½ t _j½ для остальных коэффициентов меньше t _кр = 2,131, найденного по таблице t -распределения при a=2 Q =0,05 и n=15.

Исключив из модели переменную x ⁽³⁾, которой соответствует минимальное значение t ₃=0,35 и получим уравнение регрессии:

(2.9)

В полученном уравнении статистически не значим и экономически не интерпретируем коэффициент при x ⁽⁵⁾. Исключив x ⁽⁵⁾ получим уравнение регрессии:

(2.10)

Мы получили значимое уравнение регрессии со значимыми и интерпретируемыми коэффициентами.

Однако полученное уравнение является не единственно “хорошей” и не “самой лучшей” моделью урожайности в нашем примере.

Покажем, что в условии мультиколлинеарности пошаговый алгоритм с включением переменных является более эффективным. На первом шаге в модель урожайности y входит переменная x ⁽⁴⁾, имеющая самый высокий коэффициент корреляции с y, объясняемой переменной - r (y, x ⁽⁴⁾)=0,58. На втором шаге, включая уравнение наряду с x ⁽⁴⁾ переменные x ⁽¹⁾ или x ⁽³⁾, мы получим модели, которые по экономическим соображениям и статистическим характеристикам превосходят (2.10):

(2.11)

и

(2.12)

Включение в уравнение любой из трех оставшихся переменных ухудшает его свойства. Смотри, например, уравнение (2.9).

Таким образом, мы имеем три “хороших” модели урожайности, из которых нужно выбрать по экономическим и статистическим соображениям одну.

По статистическим критериям наиболее адекватна модель (2.11). Ей соответствуют минимальные значения остаточной дисперсии =2,26 и средней относительной ошибки аппроксимации и наибольшие значения и F_набл = 273.

Несколько худшие показатели адекватности имеет модель (2.12), а затем — модель (2.10).

Будем теперь выбирать наилучшую из моделей (2.11) и (2.12). Эти модели отличаются друг от друга переменными x ⁽¹⁾ и x ⁽³⁾. Однако в моделях урожайностей переменная x ⁽¹⁾ (число колесных тракторов на 100 га) более предпочтительна, чем переменная x ⁽³⁾ (число орудий поверхностной обработки почвы на 100 га), которая является в некоторой степени вторичной (или производной от x ⁽¹⁾).

В этой связи из экономических соображений предпочтение следует отдать модели (2.12). Таким образом, после реализации алгоритма пошагового регрессионного анализа с включением переменных и учета того, что в уравнение должна войти только одна из трех связанных переменных (x ⁽¹⁾, x ⁽²⁾ или x ⁽³⁾) выбираем окончательное уравнение регрессии:

Уравнение значимо при a=0,05, т.к. F_набл = 266 > F_kp = 3,20, найденного по таблице F -распределения при a= Q =0,05; n₁=3 и n₂=17. Значимы и все коэффициенты регрессии и в уравнении ½ t _j½> t _kp(a=2 Q =0,05; n=17)=2,11. Коэффициент регрессии q₁ следует признать значимым (q₁¹0) из экономических соображений, при этом t ₁=2,09 лишь незначительно меньше t _kp = 2,11.

Из уравнения регрессии следует, что увеличение на единицу числа тракторов на 100 га пашни (при фиксированном значении x ⁽⁴⁾) приводит к росту урожайности зерновых в среднем на 0,345 ц/га.

Приближенный расчет коэффициентов эластичности э₁»0,068 и э₂»0,161 показывает, что при увеличении показателей x ⁽¹⁾ и x ⁽⁴⁾ на 1% урожайность зерновых повышается в среднем соответственно на 0,068% и 0,161%.

Множественный коэффициент детерминации свидетельствует о том, что только 46,9% вариации урожайности объясняется вошедшими в модель показателями (x ⁽¹⁾ и x ⁽⁴⁾), то есть насыщенностью растениеводства тракторами и удобрениями. Остальная часть вариации обусловлена действием неучтенных факторов (x ⁽²⁾, x ⁽³⁾, x ⁽⁵⁾, погодные условия и др.). Средняя относительная ошибка аппроксимации характеризует адекватность модели, так же как и величина остаточной дисперсии . При интерпретации уравнения регрессии интерес представляют значения относительных ошибок аппроксимации . Напомним, что — модельное значение результативного показателя, характеризует среднее для совокупности рассматриваемых районов значение урожайности при условии, что значения объясняющих переменных x ⁽¹⁾ и x ⁽⁴⁾ зафиксированы на одном и том же уровне, а именно x ⁽¹⁾ = x_i ⁽¹⁾ и x ⁽⁴⁾ = x_i ⁽⁴⁾. Тогда по значениям d _i можно сопоставлять районы по урожайности. Районы, которым соответствуют значения d _i >0, имеют урожайность выше среднего, а d _i <0 — ниже среднего.

В нашем примере, по урожайности наиболее эффективно растениеводство ведется в районе, которому соответствует d ₇ =28%, где урожайность на 28% выше средней по региону, и наименее эффективно — в районе с d ₂₀ =-27,3%.

Задачи и упражнения

2.1. Из генеральной совокупности (y, x ⁽¹⁾,..., x ^(p)), где y имеет нормальный закон распределения с условным математическим ожиданием и дисперсией s², взята случайная выборка объемом n, и пусть (y_i, x_i ⁽¹⁾,..., x_i ^(p)) - результат i -го наблюдения (i =1, 2,..., n). Определить: а) математическое ожидание МНК-оценки вектора q; б) ковариационную матрицу МНК-оценки вектора q; в) математическое ожидание оценки .

 

2.2. По условию задачи 2.1 найти математическое ожидание суммы квадратов отклонений, обусловленных регрессией, т.е. EQ_R, где

.

 

2.3. По условию задачи 2.1 определить математическое ожидание суммы квадратов отклонений, обусловленных остаточной вариацией относительно линий регрессии, т.е. EQ _ост, где

.

 

2.4. Доказать, что при выполнении гипотезы Н₀: q=0 статистика

имеет F-распределение с числами степеней свободы n₁=p+1 и n₂=n-p-1.

 

2.5. Доказать, что при выполнении гипотезы Н₀: q_j=0 статистика имеет t-распределение с числом степеней свободы n=n-p-1.

 

2.6. На основании данных (табл.2.3) о зависимости усушки кормового хлеба (y) от продолжительности хранения (x) найти точечную оценку условного математического ожидания в предположении, что генеральное уравнение регрессии - линейное.

 

Таблица 2.3.

Продолжительность хранения (ч) (x)
Усушка (% к весу горячего хлеба) (y)	1,6	2,4	2,8	3,2	3,3

 

Требуется: а) найти оценки и остаточной дисперсии s² в предположении, что генеральное уравнение регрессии имеет вид 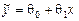; б) проверить при a=0,05 значимость уравнения регрессии, т.е. гипотезу Н₀: q=0; в) с надежностью g=0,9 определить интервальные оценки параметров q₀, q₁; г) с надежностью g=0,95 определить интервальную оценку условного математического ожидания при х ₀=6; д) определить при g=0,95 доверительный интервал предсказания в точке х =12.

 

2.7. На основании данных о динамике темпов прироста курса акций за 5 месяцев, приведенных в табл. 2.4.

Таблица 2.4.

месяцы (x)
y (%)

 

и предположения, что генеральное уравнение регрессии имеет вид , требуется: а) определить оценки и параметров уравнения регрессии и остаточной дисперсии s²; б) проверить при a=0,01 значимость коэффициента регрессии, т.е. гипотезы H₀: q₁=0;

в) с надежностью g=0,95 найти интервальные оценки параметров q₀ и q₁; г) с надежностью g=0,9 установить интервальную оценку условного математического ожидания при x ₀=4; д) определить при g=0,9 доверительный интервал предсказания в точке x =5.

 

2.8. Результаты исследования динамики привеса молодняка приведены в табл.2.5.

Таблица 2.5.

Возраст (недели) (x)
Вес (кг) (y)	1,2	2,5	3,9	5,2	6,4	7,7	9,2

 

Предполагая, что генеральное уравнение регрессии - линейное, требуется: а) определить оценки и параметров уравнения регрессии и остаточной дисперсии s²; б) проверить при a=0,05 значимость уравнения регрессии, т.е. гипотезы H₀: q=0;

в) с надежностью g=0,8 найти интервальные оценки параметров q₀ и q₁; г) с надежностью g=0,98 определить и сравнить интервальные оценки условного математического ожидания при x ₀=3 и x ₁=6;

д) определить при g=0,98 доверительный интервал предсказания в точке x =8.

 

2.9. Себестоимость (y) одного экземпляра книги в зависимости от тиража (x) (тыс.экз.) характеризуется данными, собранными издательством (табл.2.6). Определить МНК-оценки и параметров уравнения регрессии гиперболического вида , с надежностью g=0,9 построить доверительные интервалы для параметров q₀ и q₁, а также условного математического ожидания при x =10.

Таблица 2.6.

тираж (x) (тыс.экз.)
себестоимость (y)	9,10	5,30	4,11	2,83	2,11	1,62	1,41	1,30

 

2.10. Данные о расходе электроэнергии (кВт/ч) на изготовление одной тонны цемента (y) в зависимости от объема выпуска (x) продукции (тыс.т) цементными заводами приводятся в табл. 2.7.

Таблица 2.7.

Выпуск продукции x (тыс.т)
Расход электроэнергии у (кВт/ч)	10,0	8,2	7,3	6,3	6,4	5,2

 

Определить оценки и параметров уравнения регрессии вида , проверить при a=0,05 гипотезу Н₀: q₁=0 и построить с надежностью g=0,9 доверительные интервалы для параметров q₀ и q₁ и условного математического ожидания при x =20.

 

2.11. В табл. 2.8 представленные данные о темпах прироста (%) следующих макроэкономических показателей n =10 развитых стран мира за 1992г.: ВНП - x ⁽¹⁾, промышленного производства - x ⁽²⁾, индекса цен - x ⁽³⁾.

Таблица 2.8.

Страны	x (1)	x (2)	x (3)
Япония	3,5	4,3	2,1
США	3,1	4,6	3,9
Германия	2,2	2,0	3,4
Франция	2,7	3,1	2,9
Италия	2,7	3,0	5,6
Великобритания	1,6	1,4	4,0
Канада	3,1	3,4	3,0
Австралия	1,8	2,6	4,0
Бельгия	2,3	2,6	3,4
Нидерланды	2,3	2,4	3,5

 

Примем за объясняемую величину (у) показатель x ⁽¹⁾, а за объясняющую (х) переменную x ⁽²⁾ и предположим, что уравнение регрессии имеет вид:

1. .

2. .

3. .

Требуется: а) определить (с учетом линеаризации уравнения) МНК-оценки и параметров уравнения регрессии, оценку остаточной дисперсии; б) проверить при a=0,05 значимость коэффициента регрессии, т.е. Н₀: q₁=0; в) с надежностью g=0,9 найти интервальные оценки q₀ и q₁; г) найти при g=0,95 доверительный интервал для в точке х ₀= х_i, где i =5; д) сравнить статистические характеристики уравнений регрессий: 1, 2 и 3.

 

2.12. Задачу 2.11 решить, приняв за объясняемую величину (у) показатель x ⁽¹⁾, а за объясняющую (х) переменную x ⁽³⁾.

 

 

 

Список рекомендуемой литературы

1. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики: Учебник. М., ЮНИТИ, 1998 (2-е издание 2001);

 

2. Айвазян С.А., Мхитарян В.С. Прикладная статистика в задачах и упражнениях: Учебник. М. ЮНИТИ – ДАНА, 2001;

 

3. Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика. Исследование зависимостей. М., Финансы и статистика, 1985, 487с.;

 

4. Айвазян С.А., Бухштабер В. М., Енюков И.С., Мешалкин Л.Д. Прикладная статистика. Классификация и снижение размерностей. М., Финансы и статисика, 1989, 607с.;

 

5. Джонстон Дж. Эконометрические методы, М.: Статистика, 1980, 446с.;

 

6. Дубров А.В., Мхитарян В.С., Трошин Л.И. Многомерные статистические методы. М., Финансы и статистика, 2000;

 

7. Мхитарян В.С., Трошин Л.И. Исследование зависимостей методами корреляции и регрессии. М., МЭСИ, 1995, 120с.;

 

8. Мхитарян В.С., Дубров А.М., Трошин Л.И. Многомерные статистические методы в экономике. М., МЭСИ, 1995, 149с.;

 

9. Дубров А.М., Мхитарян В.С., Трошин Л.И. Математическая статистика для бизнесменов и менеджеров. М., МЭСИ, 2000, 140с.;

 

10. Лукашин Ю.И. Регрессионные и адаптивные методы прогнозирования: Учебное пособие, М., МЭСИ, 1997.

 

11. Лукашин Ю.И. Адаптивные методы краткосрочного прогнозирования. ‑ М., Статистика, 1979.

 

 

ПРИЛОЖЕНИЯ

Приложение 1. Варианты заданий для самостоятельных компьютерных исследований.

⇐ Предыдущая123

Поделиться:

Воспользуйтесь поиском по сайту: