Главная | Обратная связь | Поможем написать вашу работу!

Глава 2. Регрессионный анализ (классическая модель)

Регрессионная модель производительности труда

По данным годовых отчетов десяти (n =10) машиностроительных предприятий провести регрессионный анализ зависимости производительности труда у (тыс. руб. на чел.) от объема производства х (млн.руб.). Предполагается линейная модель, т.е. .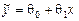

Таблица 2.1.

Исходная информация для анализа и результаты расчетов

номер п/п (i)	y_i	x_i
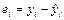
	2,1		2,77	-0,67
	2,8		3,52	-0,72
	3,2		4,27	-1,07
	4,5		4,27	0,23
	4,8		4,27	0,53
	4,9		4,27	0,63
	5,5		5,02	0,48
	6,5		5,77	0,73
	12,1		11,75	0,35
	15,1		15,50	-0,4

Решение: Определим вектор оценок коэффициентов регрессии. Согласно методу наименьших квадратов, вектор b получается из выражения:

(2.1)

Воспользовавшись правилами умножения матриц будем иметь

В матрице число 10, лежащее на пересечении 1-й строки и 1-го столбца, получено как сумма произведений элементов 1-й строки матрицы Х^Т и 1-го столбца матрицы Х, а число 75, лежащее на пересечении 1-й строки и 2-го столбца - как сумма произведений элементов 1-й строки матрицы Х^Т и 2-го столбца матрицы Х и т.д.

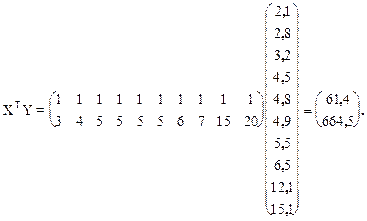
Найдем обратную матрицу

Тогда вектор оценок коэффициентов регрессии равен

а оценка уравнения регрессии будет иметь вид

(2.2)

Перейдем к статистическому анализу полученного уравнения регрессии: проверке значимости уравнения и его коэффициентов, исследованию абсолютных и относительных ошибок аппроксимации.

Предварительно определим вектор модельных значений результативного показателя :

Тогда

(2.3)

А несмещенная оценка остаточной дисперсии равна:

а оценка среднеквадратического отклонения

Проверим на уровне значимости a=0,05 значимость уравнения регрессии, т.е гипотезу H₀: q=0 (q₀=q₁=0). Для этого вычисляем величину

(2.4)

По таблице F-распределения для a=0,05, n₁=2 и n₂=8 находим F_кр=4,46. Так как F_набл>F_кр, то уравнение является значимым.

Найдем оценку ковариационной матрицы вектора :

(2.5)

Отсюда получаем несмещенные оценки дисперсий и среднеквадратических отклонений коэффициентов регрессии:

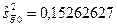
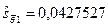
Для проверки значимости коэффициента регрессии, т.е. гипотезы Н₀: q₁=0, находим по таблице t-распределения при a=0,05, n=8 значение t_кр=2,31:

(2.6)

Так как больше t_кр=2,31, то коэффициент регрессии q₁ значимо отличается от нуля. Таким образом, окончательное уравнение регрессии имеет вид

Определим интервальные оценки коэффициентов уравнения с доверительной вероятностью g=0,95. Т.к.

(2.7)

где j=0; 1, то

q₀Î[0,525 ± 2,31´0,391], откуда -0,378 £ q₀ £ 1,428 и

q₁Î[0,74861 ± 2,31´0,0428], откуда 0,650 £ q₁ £ 0,847.

Приведенные неравенства подтверждают вывод о значимости q₁ (q₁¹ 0). В то же время коэффициент q₀ уравнения (2.2) не значим (границы доверительного интервала имеют разные знаки).

Регрессионная модель урожайности зерновых культур

По данным n =20 сельскохозяйственных районов региона требуется построить регрессионную модель урожайности на основе следующих показателей:

y — урожайность зерновых культур (ц/га);

x ⁽¹⁾— число колесных тракторов (приведенной мощности) на 100 га;

x ⁽²⁾— число зерноуборочных комбайнов на 100 га;

x ⁽³⁾— число орудий поверхностной обработки почвы на 100 га;

x ⁽⁴⁾— количество удобрений, расходуемых на гектар (т/га);

x ⁽⁵⁾— количество химических средств защиты растений, расходуемых на гектар (ц/га).

Исходные данные для анализа приведены в табл.2.1.

Таблица 2.1

Исходные данные для анализа

i	y _i	x _i⁽¹⁾	x _i⁽²⁾	x _i⁽³⁾	x _i⁽⁴⁾	x _i⁽⁵⁾
	9.70	1.59	0.26	2.05	0.32	0.14
	8.40	0.34	0.28	0.46	0.59	0.66
	9.00	2.53	0.31	2.46	0.30	0.31
	9.90	4.63	0.40	6.44	0.43	0.59
	9.60	2.16	0.26	2.16	0.39	0.16
	8.60	2.16	0.30	2.69	0.37	0.17
	12.50	0.68	0.29	0.73	0.42	0.23
	7.60	0.35	0.26	0.42	0.21	0.08
	6.90	0.52	0.24	0.49	0.20	0.08
	13.50	3.42	0.31	3.02	1.37	0.73
	9.70	1.78	0.30	3.19	0.73	0.17
	10.70	2.40	0.32	3.30	0.25	0.14
	12.10	9.36	0.40	11.51	0.39	0.38
	9.70	1.72	0.28	2.26	0.82	0.17
	7.00	0.59	0.29	0.60	0.13	0.35
	7.20	0.28	0.26	0.30	0.09	0.15
	8.20	1.64	0.29	1.44	0.20	0.08
	8.40	0.09	0.22	0.05	0.43	0.20
	13.10	0.08	0.25	0.03	0.73	0.20
	8.70	1.36	0.26	0.17	0.99	0.42

Решение. Предварительно, с целью анализа взаимосвязи показателей построена матрица парных коэффициентов корреляции .

Таблица 2.2.

⇐ Предыдущая 123 Следующая ⇒

Воспользуйтесь поиском по сайту: