 |
Сходящиеся числовые последовательности
|
|
|
|
ГЛАВА 2. ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
Определение 1. Функция, определенная на множестве N натуральных чисел и принимающая значения из множества Х 
R называется числовой последовательностью. Обозначается 
.Множество значений числовой последовательности 
обозначается 
.
Примеры.
1. 
, 
-множество значений есть рациональные числа вида 
, где n 
N;
2. хn= 1-(-1 )n, { хn }={2, 0, 2, 0,…}- множество значений состоит из двух чисел: 0 и 2.
3. хn=а=const, постоянная последовательность, множество значений состоит из одного числа а.
Определение 2. Числовая последовательность хn называется сходящейся, если существует число х0, такое, что для любого 
найдется номер члена числовой последовательности N, такой, что при всех 
имеет место неравенство: 
Символически это определение записывают следующим образом:
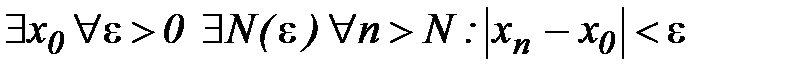(1)
Число х0 называется пределом последовательности хn. Говорят также, что последовательность { хn } сходится к числу х0. Обозначение: 
или 
.
Если последовательность не сходится ни к одному числу, то она называется расходящейся.
Геометрический смысл понятия предела состоит в том, что при произвольно заданном положительном числе 
можно указать номер члена последовательности 
, начиная с которого все члены последовательности окажутся в произвольной, сколь угодно малой ε - окрестности точки 
Построим отрицание определения существования предела, т.е. построим определение расходящейся числовой последовательности. Числовая последовательность { хn } называется расходящейся, если
Здесь мы воспользовались правилом построения отрицания с кванторами: квантор 
надо заменить на 
, а квантор на и после двоеточия изменить знак неравенства.
Примеры.
|
|
|
1. Пусть 
. Показать, что 
.
Решение. Действительно, неравенство 
, будет выполняться при n >[ 
]. Таким образом, N (ε)= [ ] и число 
является пределом последовательности.
Замечание. Функцией y= [ x ] называется целая часть числа x, т.е. наибольшее
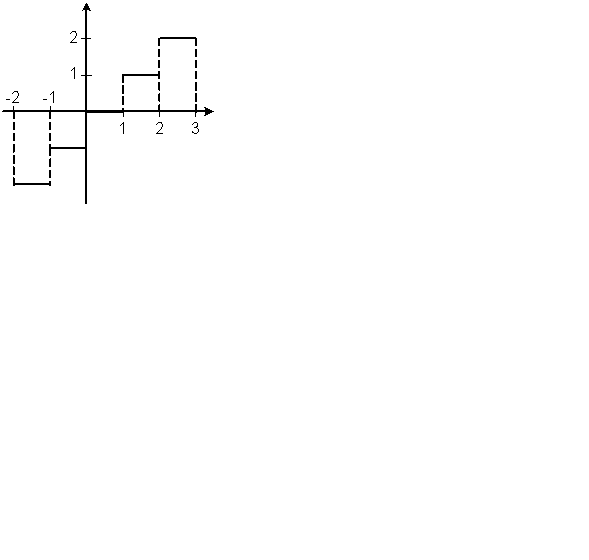
Рис.2.1.
целое число n, удовлетворяющее неравенству n ≤ х (рис.2.1). Например,
[1,8] = 1, [-5,3] = - 6.
2. Показать, что эта последовательность 
расходится.
Решение. От противного. Пусть предел существует, т.е. х0, что при n > N (ε): | хn – х0 | < ε. Возьмем число ε = 
.Если n – четное, то хn =1 и | 1 – х0 | < ε = , откуда
< х < 
. (*)
Если n – нечетное, 
, откуда
- < х0 <- . (**)
Отсюда ясно, что не существует такого х0, чтобы неравенства (*) и (**) выполнялись одновременно при произвольном ε. Таким образом, последовательность {(-1) n }-расходится.
Теорема 1 (о единственности предела). Всякая сходящаяся последовательность имеет только один предел.
□ Предположим противное, т.е. хn имеет два предела а и b, а ≠ b. По определению предела, каково бы ни было ε>0 N1 и N2, что | х n – а | < ε 
и 
. Выберем 
. Тогда при 
одновременно имеют место неравенства:
и 
Тогда
Получили противоречие, т.е. предположение неверно и теорема доказана. ■
Определение 3. Последовательность хn называется ограниченной, если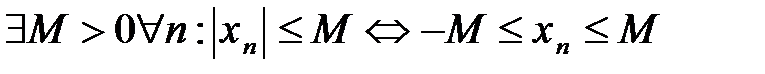 
.В противном случае последовательность называется неограниченной.
Например, последовательность 
ограниченная, а последовательность 
неограниченная.
Теорема 2. Сходящаяся последовательность ограничена.
□ Пусть хn сходящаяся последовательность, а х0 – её предел. Выберем ε >0 произвольно. По определению 2,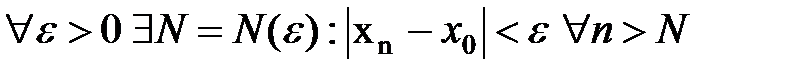 
. Тогда при 
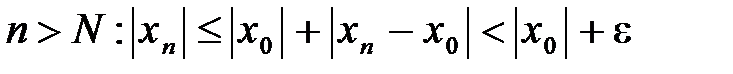, т.е. хn – ограничена при n > N. Положим 
. Очевидно, n | хn | ≤ М, следовательно множество { хn } ограничено и последовательность ограничена. ■
Замечание. Из ограниченности последовательности её сходимость не вытекает. Например, последовательность хn =(-1)n - ограничена, но расходится. Если последовательность неограниченна, то она расходится, т.к. не выполняется определение 2.
|
|
|
Пример. Исследовать сходимость последовательности 
в зависимости от значения параметра q.
Решение. Если | q |<1, то 
. Действительно,
Если 
при 
;
если ε > 1, то | qn | <ε при N =1.
Теперь, если q =1, то 
, т.к. 
если q =-1, то последовательность хn =(-1)n расходится (установлено ранее);
если | q | > 1, то последовательность расходится, т.к. она не ограничена.
Таким образом, 
Например, 
.
Определение 4. Последовательность хn называется неубывающей (невозрастающей), если 
. Неубывающие и невозрастающие последовательности называются монотонными.
Определение 5. Последовательность хn называется возрастающей (убывающей), если 
.Возрастающие и убывающие последовательности называются строго монотонными.
Теорема 3. Всякая монотонная ограниченная последовательность сходится.
□Пусть хn не убывает, т.е. 
. По условию теоремы последовательность { хn } ограничена, т.е. множество Х её значений ограничено. Тогда, в силу известной теоремы из главы 1, существует точная верхняя грань множества Х. Пусть 
. Т.к. х0 – точная верхняя грань, то по определению имеем:
1) 
;
2) ε >0 
.
В силу монотонности хn: 
. А это, если справа добавить + ε, то получим определение сходящейся числовой последовательности, т.е. 
, что и требовалось доказать. Для не возрастающей последовательности доказательство аналогичное. ■
|
|
|
