 |
Арифметические свойства сходящихся последовательностей
|
|
|
|
Пусть хn и yn – две числовые последовательности.
Определение 6. Суммой, разностью, произведением последовательности на число, произведением, частным двух последовательностей хn и yn называется следующие последовательности: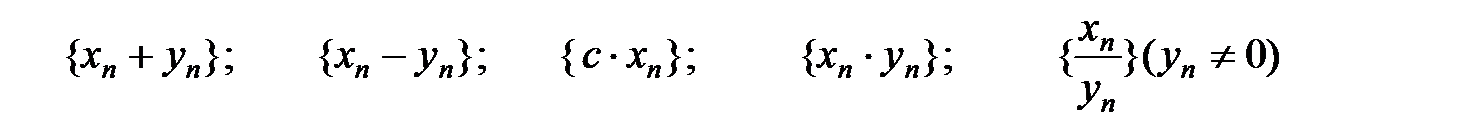 
.
Теорема 4. Пусть последовательности 
и 
сходятся, и 
, 
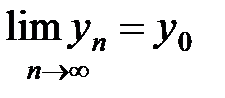. Тогда сходятся и последовательности 
, 
, 
, 
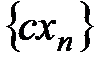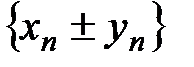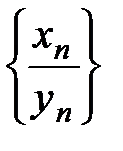(с =const, 
в последнем случае), причем пределы вычисляются по формулам:
а) 
;
б)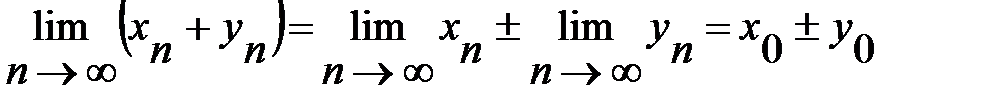 
;
в) 
= 
;
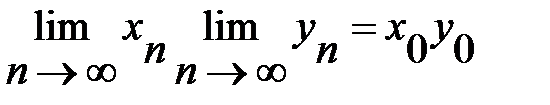г) 
, 
.
□ а) Покажем, что последовательность 
имеет предел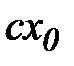 
. По определению предела, пусть 
- произвольное положительное число. Возьмем число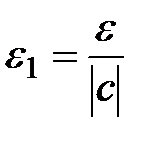 
(если с=0, то утверждение а) очевидно). Тогда существует такой 
, что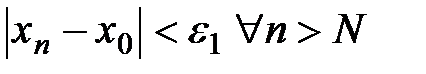 
. Откуда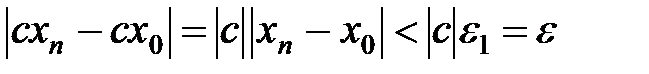 
.
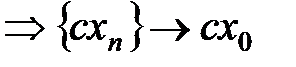б) По условию, т.к. пределы существуют, то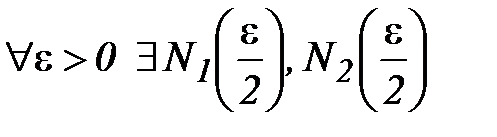 
такие, что выполняются неравенства 
Чтобы оба неравенства выполнялись одновременно положим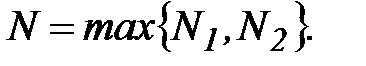 
, тогда
Таким образом,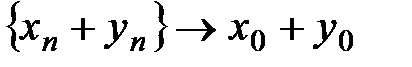 
.
в) Поскольку последовательност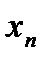и 
и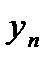 
сходятся, то они ограничены, в частности, существует такое число М, что выполняется неравенство: 
. Увеличивая число М, можно получить неравенство 
. Поскольку последовательности сходятся, то по определению: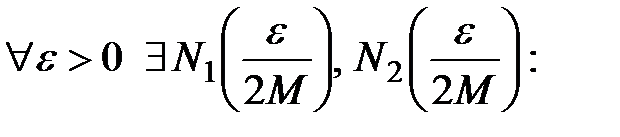 
.
Возьмем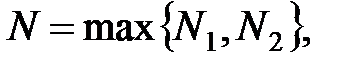 
тогда получим
г) Покажем сначала, что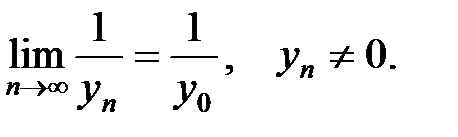 
Поскольку последовательность 
сходится, то для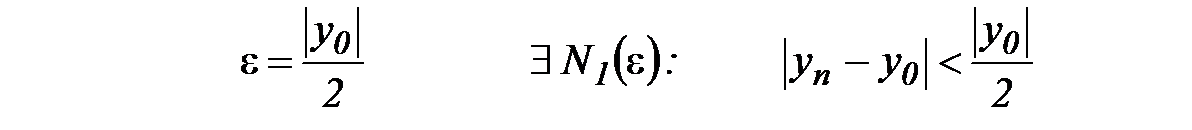 
.
Тогда
.
Снова, так как сходится, то по определению
.
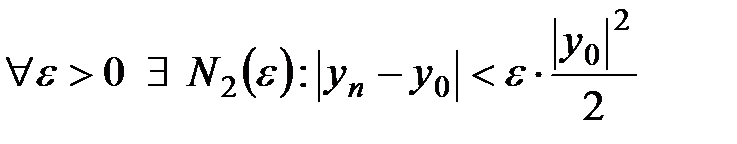Выберем число 
Тогда
т.е.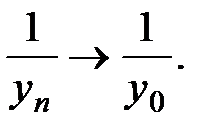 
Отсюда, по утверждению в):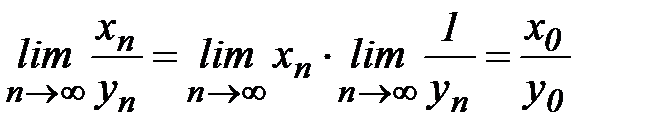 
. ■
Теорема 5 (сравнения, предельный переход в неравенствах). Пусть заданы последовательности 
, 
, 
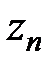.Тогда,
а) если 
и последовательности 
, 
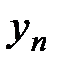сходятся, то выполняется неравенство: 
.
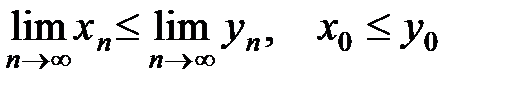б) если 
и последовательности 
и 
сходятся к одному пределу, то также сходится, причем к тому же пределу, т.е.
.
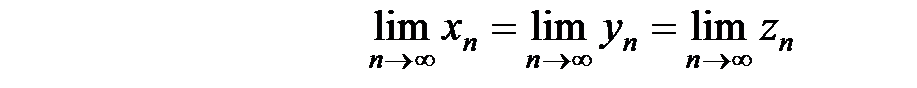□ а) Пусть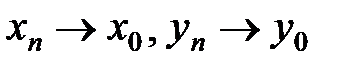 
. Докажем, что 
. От противного. Пусть 
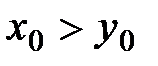. По определению, возьмем 
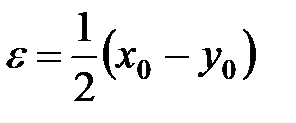. Тогда
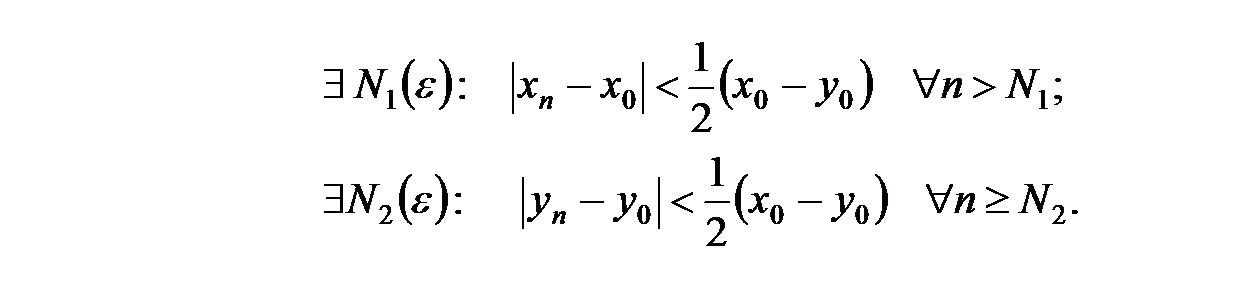
Обозначим число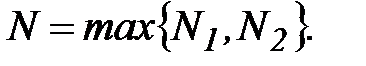 
Тогда 
Откуда 
. Пришли к противоречию, таким образом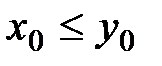 
.
|
|
|
б) Пусть 
, тогда по определению предела
.
Возьмем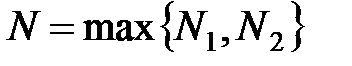 
. Тогда 
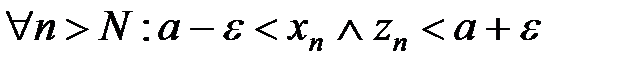, но по условию теоремы: 
.
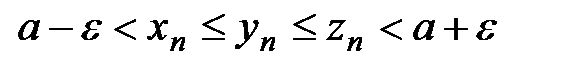
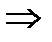
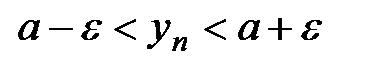Таким образом,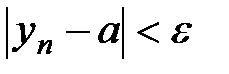 
, а это означает, что 
. ■
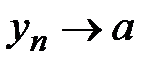Примеры. 1. Показать, что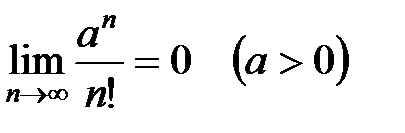 
.
Решение. Возьмем номер N члена последовательности такой, чтобы 
.Тогда,при 
. Откуда справедливо неравенство:
. (2)
Т.к.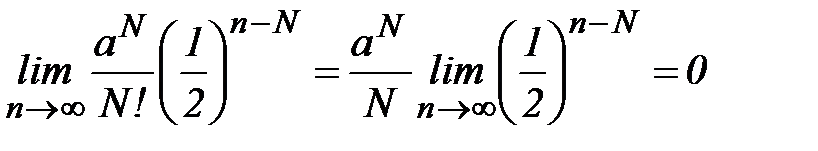 
, 
, то, в силу утверждения б) теоремы 5 из (2): 
, так как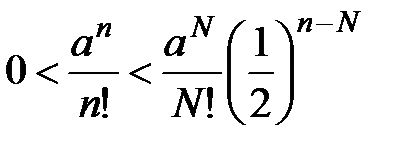 
,
(
).
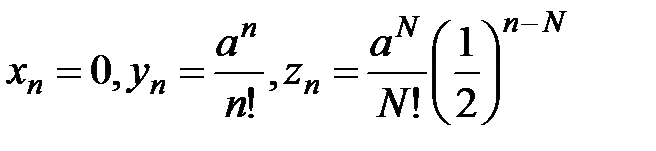2. Доказать, что при 
.
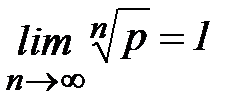Решение. Пусть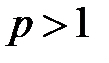 
. Положим 
, причем 
по формуле бинома 
. Переходя в этом неравенстве к пределу, получаем
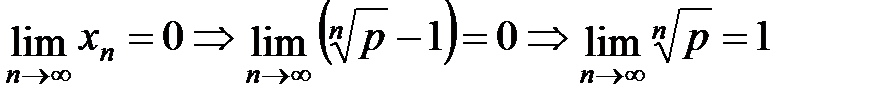
Если 
, то равенство очевидно. Если 
, то надо перейти к обратным числам,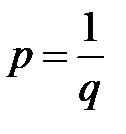 
, где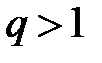 
.
3.Доказать, что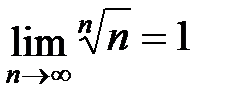 
.
Решение. Положим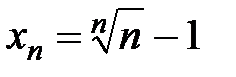 
. Тогда 
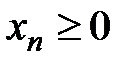и 
, 
при 
.
Тогда по теореме сравнения 
.
Определение 7. Последовательность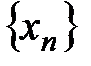 
называется бесконечно малой (б. м.), если 
.
Очевидно, что если 
, то последовательность 
бесконечно малая. Наоборот, если 
, где 
, то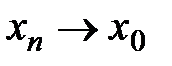 
. Действительно,
.
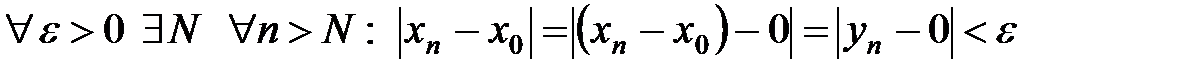Теорема 6. Произведение ограниченной последовательности на бесконечно малую есть бесконечно малая последовательность.
□ Пусть 
– бесконечно малая, а 
– ограниченная последовательность. Это означает, что 
и 
.
Тогда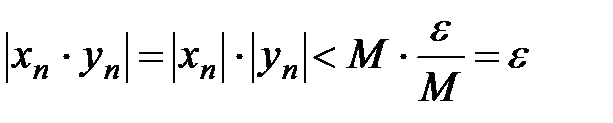 
, 
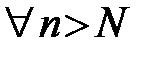, т.е. 
. ■
Определение 8. Последовательность 
называется бесконечно большой, если
.
В этом случае, если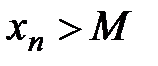 
, то пишут 
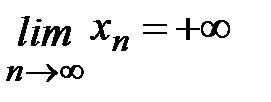, ес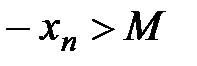ли 
или 
, то пишут 
.
Теорема 7. а) Есл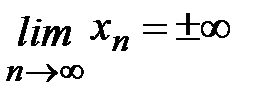и 
и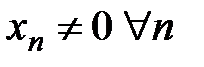 
, то последовательность 
– бесконечно малая;
б) если 
, то последовательность 
- бесконечно большая.
□ а) Пусть 
. Тогда для последовательности 
имеем: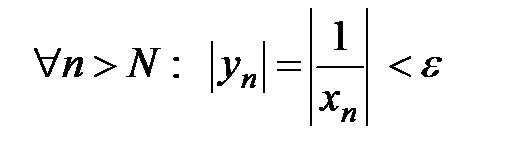 
, т. е. 
– бесконечно малая.
б) Доказать самостоятельно. ■
В заключение докажем теорему, которая определяет число e, играющее очень важную роль в математике.
Теорема 8. Последовательность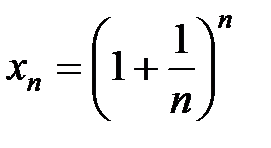 
имеет предел.
□ Сначала заметим, что при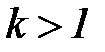 
выполняется неравенство
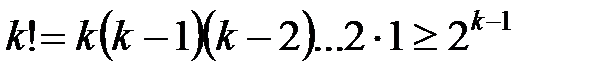или 
. (3)
Воспользуемся формулой бинома Ньютона:
При а=1, b=1/n получим:
Последовательность 
с ростом n возрастает, т.к. увеличивается каждый член суммы, а число членов всякий раз увеличивается на единицу, т.е. не убывает и ограничена. Тогда по теореме 3последовательность сходится.
|
|
|
■
Следуя Эйлеру, предел этой последовательности обозначают через e. Таким образом, записывают:
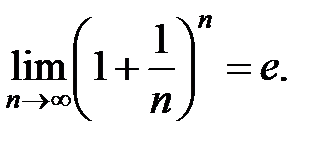
Известно, что (способ вычисления покажем в дальнейшем): e = 2,71828 …
Постоянное число e называют числом Д.Непера (1550-1617). Логарифм числа а по основанию e называется натуральным логарифмом числа а и обозначается символом a.
|
|
|
