 |
Теорема Больцано-Вейерштрасса. Фундаментальные
|
|
|
|
Последовательности
Больцано Бернар (чещс. 1781-1848), Вейерштрасс Карл (1815-1897).
Определение 9. Пусть 
- числовая последовательность и 
- возрастающая последовательность натуральных чисел. Последовательность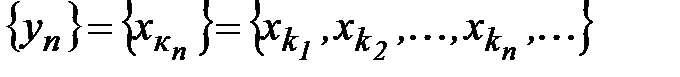 
называется подпоследовательностью последовательности 
.
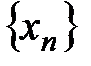Если подпоследовательность 
сходится, то ее предел называется частичным пределом последовательности 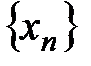. Например, последовательность 
не сходится, т.е. расходится. Ее подпоследовательность 
расходится, а 
сходится.
Теорема 9. Если последовательность 
сходится, то любая ее подпоследовательность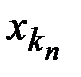 
также сходится и имеет тот же предел.
□ Пусть 
и 
, тогда 
. Очевидно, 
. Это значит, что 
. ■
Теорема 10 (о вложенных отрезках). Пусть 
- последовательность вложенных отрезков, т.е.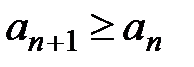 
, 
и 
или 
. Тогда существует по меньшей мере одна точка, принадлежащая всем отрезкам одновременно.
□ По условию последовательность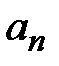 
не убывает, а 
не возрастает. Также по условию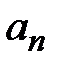 
и 
ограничены, т.к. 
. Тогда по теореме 3существуют 
и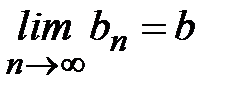 
. Причем 
(по теореме сравнения).Очевидно, что 
. Т.о., точки 
и 
принадлежат всем вложенным отрезкам (они могут и совпадать). ■
Теорема 11 (Больцано - Вейерштрасс). Из всякой ограниченной можно выделить сходящуюся подпоследовательность.
□ Пусть последовательность 
ограничена. Это означает, что 
, т.е. все значения 
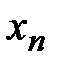лежат на отрезке 
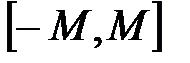.Обозначим для удобства этот отрезок как 
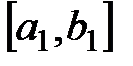. Разделим его пополам. По крайней мере, один из полученных отрезков содержит бесконечное число членов последовательности 
(или оба).
Выберем ту часть отрезка 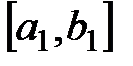, где 
- бесконечное множество, и обозначим ее через 
. Отрезок снова делим пополам и выбираем ту половину, где членов числовой последовательности 
бесконечно много и обозначаем ее 
и т.д. Получим последовательность вложенных отрезков. Причем длина отрезков равна:
|
|
|
, 
.
В силу теоремы 10, существует точка с, которая принадлежит всем отрезкам:
(4)
Построим подпоследовательность сходящуюся к числу с. В качестве 
возьмем любой член последовательности 
. В качестве 
возьмем элемент последовательности 
, лежащий на , у которого 
(т.к. на членов последовательности бесконечно много, то так всегда можно выбрать). В качестве 
возьмем элемент последовательности 
из отрезка 
, у которого 
:
(5)
Покажем, что 
. Действительно, из (4) и (5) и геометрических соображений следуют неравенства 
. Переходя к пределу, получим 
. ■
В качестве иллюстрации к этой теореме можно взять ограниченную последовательность 
, которая расходится. Её подпоследовательность 
- сходится.
Пусть 
- ограниченная последовательность: 
. Обозначим через 
множество частичных пределов последовательности 
. Ясно, что 
(по теореме 10).Очевидно, что ограничено, т.к. если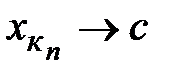 
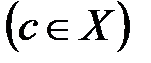, то из неравенства 
Поскольку - ограниченное множество, то 
и 
Обозначим 
, 
Теорема 12. Числа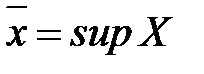 
, 
являются частичными пределами последовательности , т.е.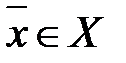 
, 
(без доказательства).
Определение 10. Числа 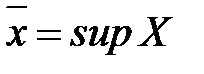и 
называются соответственно верхним и нижним пределами последовательности и обозначаются:
, 
.
Пример. Последовательность 
имеет верхний и нижний пределы 
, 
.
Определение сходимости последовательности связано с пределом 
этой последовательности, который заранее неизвестен, т.е. трудно непосредственно проверять сходимость. Поэтому желательно использовать для этого некоторые “внутренние свойства” последовательностей.
Определение 11. Последовательность 
называется фундаментальной, если
.
Ясно, что члены фундаментальной последовательности с увеличением номера сближаются между собой.
Теорема 13. Если последовательность фундаментальная, то она ограничена.
|
|
|
□ Фиксируем 
.Тогда 
. Возьмем 
, тогда 
и
.
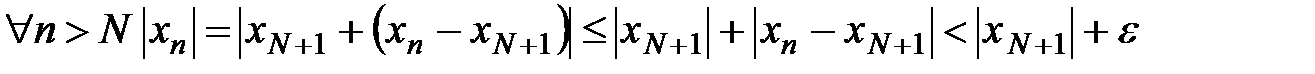Т.е. все члены 
при 
ограничены числом 
.
Положим 
. Очевидно, 
, т.е. по определению последовательность ограничена. ■
Теорема 14 (критерий Коши,1789-1857). Для того чтобы последовательность была сходящейся, необходимо и достаточно, чтобы она была фундаментальной.
□ а) Необходимость. Пусть 
сходится, - предел. Докажем, что она фундаментальная. По определению имеем:
.
Тогда
,
т.е. 
- фундаментальная.
б) Достаточность. Пусть - фундаментальная последовательность. Докажем, что она сходится.
Последовательность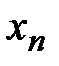 
ограничена (теорема 13).Следовательно, можно выделить подпоследовательность 
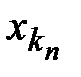, сходящуюся к некоторому числу .Покажем, что и 
сходится к .Пусть 
- произвольное положительное число. По условию теоремы, т.к. последовательность фундаментальная, то
и 
.
Поскольку 
, то из последнего неравенства при 
получим 
при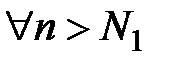 
. Подпоследовательность 
сходится, поэтому существует такой 
, что при 
выполняются неравенства: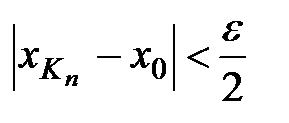 
.Пусть 
, тогда при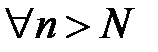 
:
Это означает, что последовательность сходится к . ■
Пример. Доказать, что последовательность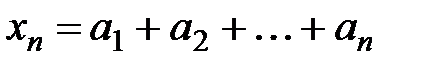 
,
где 
- произвольные вещественные числа, удовлетворяющие условию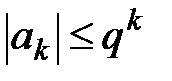 
, 
, сходится.
Решение. Пусть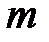 
и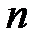 
- любые натуральные числа. Обозначим 
.
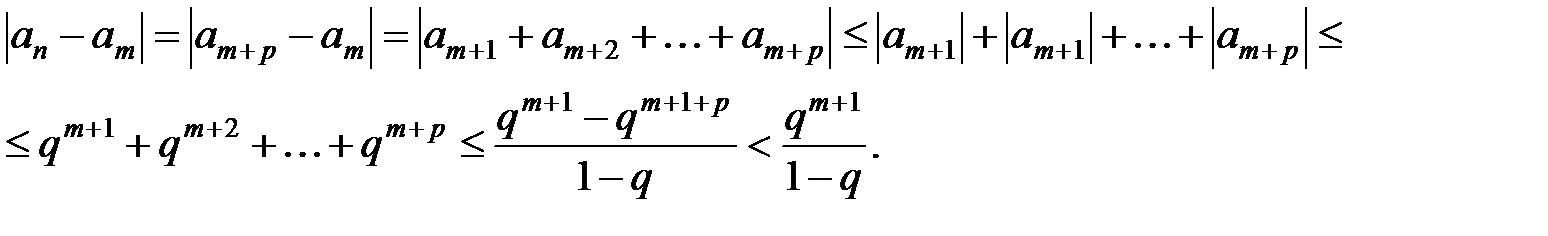
Учитывая, что последовательность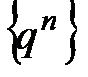 
- бесконечно малая, т.е. 
, получим, что при 
.
Числовые ряды.
Другой формой изучения числовых последовательностей являются числовые ряды. Пусть = 
- числовая последовательность.
Определение 12. Выражение вида (формально составленная сумма)
(6)
называется числовым рядом, а 
- его к - членом.
Другими словами, ряд есть бесконечная сумма членов некоторой числовой последовательности. Сумма первых n членов числовой последовательности 
называется частичной суммой ряда и обозначается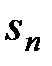 
:
.
Частичные суммы 
являются также членами числовой последовательностью и она называется последовательностью частичных сумм.
Определение 13. Числовой ряд называется сходящимся, если сходится последовательности его частичных сумм 
, т.е. если существует предел
,
который называют суммой ряда. В этом случае пишут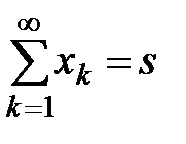 
и, следовательно,
.
Величина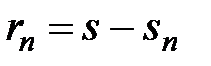 
называется остатком ряда.
Если последовательность 
расходится, то говорят, что и числовой ряд расходится.
|
|
|
Замечание. По определению 2 сходимость ряда (6) равносильна сходимости числовой последовательности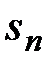 
. Наоборот, если 
некоторая числовая последовательность, то вопрос о ее сходимости равносилен сходимости ряда 
, 
, для которого частичными суммами будут как раз члены последовательности 
. Это иногда используют для доказательства сходимости рядов и последовательностей. Таким образом, числовые ряды есть новая форма изучения числовых последовательностей.
Одна из главных задач теории числовых рядов состоит в изучении вопроса о сходимости и расходимости.
Примеры. 1) Исследовать сходимость ряда 
.
Решение. Рассмотрим последовательность частичных сумм: 
, 
, 
,…., 
, 
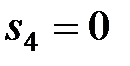,… т.е. 
. Эта последовательность не имеет предела, поэтому ряд расходится.
2) Исследовать сходимость ряда 
Решение. Составим последовательность частичных сумм 
. Так как
,
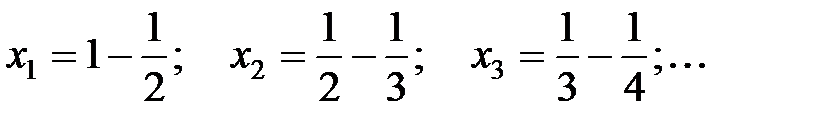
то 
.
Тогда 
,
откуда следует, что ряд сходится. Аналогичным образом можно найти сумму ряда
, где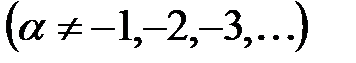 
3) Исследовать сходимость ряда 
в зависимости отпараметра q.
Решение. Частичной суммой ряда является сумма геометрической прогрессии:
Если 
не существует и ряд расходится.
При 
и ряд расходится.
При 
расходится (пример 1).
Если 
= 
, т.к. 
и ряд сходится.
4) Показать, что ряд 
расходится.
Решение. Так как частичную сумму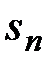 
можно записать следующим образом:
.
Тогда, т.к. 
при 
, то ряд расходится.
Пусть 
и 
- два числовых ряда.
Определение 14. Суммой и разностью этих рядов, а также произведением ряда на число называют следующие ряды:
; 
.
Теорема 15. Если ряды 
и 
сходятся, то сходится их сумма, разность и произведение на число, причем 
; 
Замечание. Отбрасывание или добавление конечного числа слагаемых к членам ряда не влияет на его сходимость или расходимость, т.к. в этом случае его частичная сумма изменится на постоянное число.
Теорема 16 (критерий Коши). Для сходимости ряда 
необходимо и достаточно, чтобы
Очевидно, что неравенство (2) равносильно следующему:
.
Следствие (необходимое условие сходимости ряда). Если ряд (6) сходится, то 
|
|
|
□ При 
получим, согласно критерия Коши, что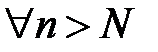 
: 
, т.е.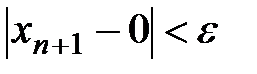 
, т.е. 
. ■
Отметим, что это условие необходимое, но не достаточное, т.е. если предел равен нулю, то ряд может сходиться, а может и расходиться.
Пример. Рассмотрим ряд 
, который называется гармоническим рядом.
Очевидно, что 
. Докажем, что ряд расходится. Воспользуемся критерием Коши. Возьмем 
и 
. Тогда
.
Следовательно, критерий Коши не выполняется и ряд расходится.
Определение 15. Числовой ряд (6) называется знакоположительным, если 
.
Если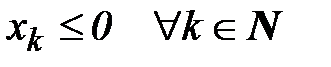 
, то ряд называется знакоотрицательным. Знакоположительные и знакоотрицательные ряды называются знакопостоянными. Для исследования сходимости знакопостоянных рядов достаточно изучать сходимость знакоположительных рядов.
Сформулируем основные достаточные признаки сходимости знакоположительных рядов.
Теорема 17 (основной признак). Для того чтобы знакоположительный ряд сходился необходимо и достаточно, чтобы его частичные суммы были ограничены сверху, т.е.
.
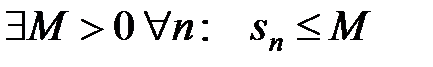Теорема 18 (признак разреженности). Пусть члены знакоположительного ряда монотонно убывают, т.е. 
Тогда ряд 
сходится тогда и только тогда, когда сходится ряд
Рассмотрим пример применения этого признака.
Пример. Ряд 
называется обобщенным гармоническим рядом. Исследуем его сходимость в зависимости от параметра α.
Решение. Если 
то частичные суммы неограниченны и ряд расходится.
Если 
то по теореме 4 этот ряд сходится одновременно с рядом
который сходится, если 
. При остальных значениях α ряд расходится. Отметим, что сумма сходящегося ряда 
называется «дзета-функцией Римана».
Теорема 19 (признак сравнения). Пусть имеются два знакоположительных ряда:
(7) 
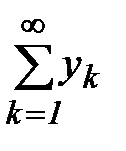(8)
причем
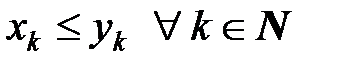. (9)
Тогда: а) если ряд (8) сходится, то сходится и ряд (7);
б) если ряд (7) расходится, то расходится и ряд (8).
Примеры. Исследовать сходимость рядов.
1) 
.
Решение. Ясно, что 
. Рассмотрим ряд 
, где 
. Поскольку 
а ряд 
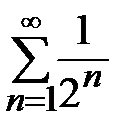- сходится как геометрическая прогрессия, следовательно, исходный ряд сходится.
2) 
.
Решение. Так как 
, а ряд 
расходится, как обобщенный гармонический ряд, следовательно, и ряд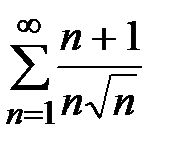 
расходится.
Теорема 20 (предельный признак сравнения). Пусть даны два знакоположительных ряда (7) и (8). Тогда, если существует конечный и отличный от нуля предел
,
то эти ряды одновременно сходятся или расходятся.
Пример. Исследовать сходимость ряда 
.
Решение. Проверим сначала необходимый признак:
.
Следовательно, ряд может сходиться, а может и расходиться. Используем достаточный признак сравнения в предельном виде
.
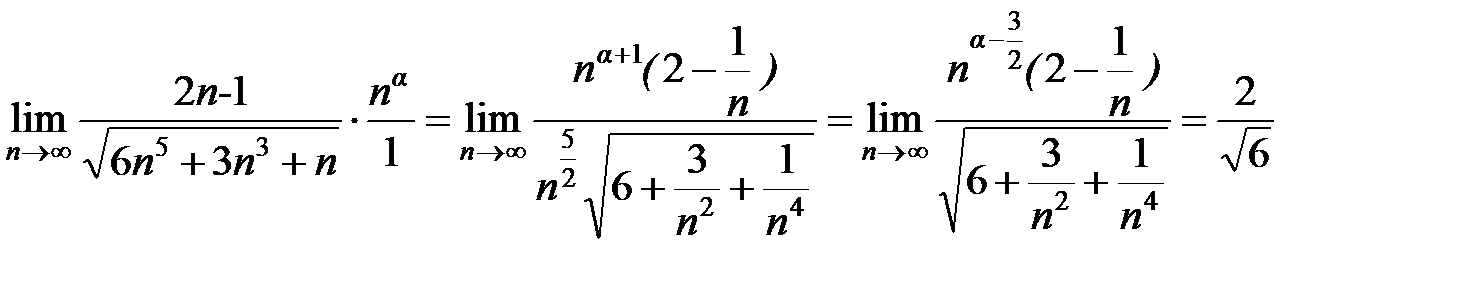Этот предел будет конечен и равен 
, когда 
, т.е. при 
Т.к. обобщенный гармонический ряд сходится, то по теореме ряд сходится.
|
|
|
Теорема 21 (признак Даламбера, фр. 1717-1783 ) Если существует предел 
,
то знакоположительный ряд 
сходится при λ< 1 и расходится при λ> 1.
Пример. Исследовать сходимость ряда 
.
Решение.
Согласно теореме, ряд расходится.
Замечание. Если 
, то ряд может сходиться, а может и расходиться.
Теорема 22 ( признак Коши, фр. 1789-1857). Если существует конечный предел
,
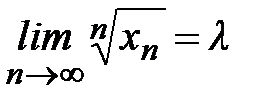то в случае 
знакоположительный ряд 
сходится, а при 
расходится.
Замечание. При λ= 1 ряд может сходиться, а может и расходиться.
Теорема 23 (интегральный признак). Пусть функция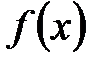 
определена на промежутке 
, неотрицательная и монотонно убывает на нем. Тогда числовой ряд 
сходится тогда и только тогда, когда сходится несобственный интеграл 
.
Замечание. Очевидно, что в условиях теоремы интеграл 
можно заменить интегралом 
, где 
- произвольное число.
Пример. Исследовать сходимость ряда 
.
Теперь снова остановимся на определении числа е, которое используется как основание для натуральных логарифмов 
. Рассмотрим ряд
Покажем, что он сходится. При 
очевидно неравенство 
.
Ряд 
есть сумма бесконечно убывающей прогрессии, он сходится и её значение равно
.
Тогда по признаку сравнения ряд 
тоже сходится. Сумма этого ряда обозначается через е:
Очевидны следующие неравенства:
Оценим погрешность, с которой частичная сумма 
приближает число е. Рассмотрим разность 
Таким образом, 
. Так, если n =6, n!=720, n! n =4320 
.
Число е с пятью знаками е ≈2,71828. Причем е – иррациональное число.
Определение 16. Числовой ряд 
называется знакопеременным, если его члены 
могут иметь как положительные, так и отрицательные знаки. Например, 
, 
.
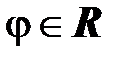Теорема 24 (достаточный признак сходимости). Если сходится ряд 
, то сходится и ряд 
.
Пример. Знакопеременный ряд 
сходится, т.к. сходится обобщенный гармонический ряд с показателем равным двум.
Определение 17. Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд из абсолютных величин его членов.
Из теоремы 10 ясно, что всякий абсолютно сходящийся ряд является просто сходящимся. Знакопеременный ряд называется условно сходящимся, если он сходится, а ряд, составленный из абсолютных величин его членов, расходится.
Пример. Знакопеременный ряд 
,(
) сходится абсолютно по признаку сравнения, т.к. 
, а ряд 
сходится.
Среди знакопеременных рядов очень важное место занимают знакочередующиеся ряды, т.е. ряды вида:
,
где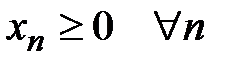 
.
Такой ряд иногда называют рядом Лейбница. Для этих рядов справедлив достаточный признак.
Теорема 25 (признак Лейбница). Пусть члены знакочередующегося ряда монотонно убывают, т.е.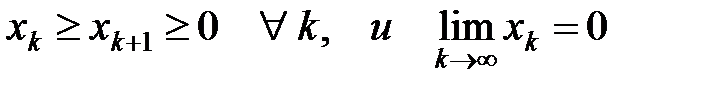 
, тогда ряд сходится.
Пример. Знакопеременный ряд 
сходится условно.
Следствие. Абсолютная погрешность при замене суммы знакочередующегося ряда его частичной суммой не превосходит первого отброшенного члена ряда, т.е.
.
Замечание. Теорема остается верной, если условие 
выполняется, начиная с некоторого натурального N.
Следствие играет большую роль в практических вычислениях с помощью рядов.
Пример. Вычислить с точностью δ =0,001 сумму ряда
.
Так как 
, то сумма будет приближенно равна 
2.5. Контрольные вопросы.
1. Сформулируйте определения: а) последовательности; б) ограниченной и неограниченной последовательности; в) предела последовательности. Дайте геометрическую интерпретацию этих определений.
2. Эквивалентно ли определение предела последовательности такому определению: 
, если 
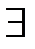положительное число K (не обязательно натуральное) такое, что 
.
3. Покажите на примере, что номер N, фигурирующий в определении предела последовательности, зависит, вообще говоря, от e.
4. Пусть последовательность 
и число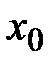 
удовлетворяют условию: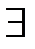 
такой, что 
и 
. Всякая ли сходящаяся к 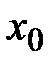последовательность удовлетворяет этому условию? Какова геометрическая интерпретация этого условия?
5.Пусть 
.
а) могут ли все члены последовательности быть положительными (отрицательными), если 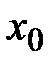=0?
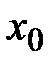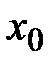б) может ли последовательность иметь бесконечно много отрицательных (равных нулю) членов, если =0; ¹0?
в) докажите, что 
; 
;
г) докажите, что ограничена.
6. Пусть в некоторой окрестности точки 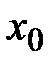лежит бесконечно много членов последовательности . Следует ли из этого условия, что: а) 
; б) никакая точка вне этой окрестности не является пределом последовательности ; в) ограничена?
7. Пусть в любой окрестности точки x0 лежит бесконечно много членов последовательности . Следует ли отсюда, что:
а) 
? б) ограничена?
8. Пусть последовательность является ограниченной (неограниченной). Следует ли из этого условия, что она сходится (расходится)?
9. Пусть последовательность сходится. Является ли сходящейся последовательность, которая получается из исходной, если:
а) из нее удалить конечное число членов, а оставшиеся заново перенумеровать в порядке их следования?
б) к ней добавить конечное число членов, перенумеровать члены последовательности в порядке их следования?
в) в ней изменить произвольным образом конечное число членов?
10. Сформулируйте определения: а) бесконечно малой последовательности; б) бесконечно большой последовательности. Дайте геометрическую интерпретацию этих определений.
11. Сформулируйте на языке "e – N " отрицание того, что последовательность является: а) бесконечно малой; б) бесконечно большой. Дайте геометрическую интерпретацию этих отрицаний.
12. Дайте определение, соответствующее символической записи 
13. а) Является ли бесконечно малая последовательность ограниченной?
б) Является ли бесконечно большая последовательность ограниченной: сходящейся?
в) Является ли любая неограниченная последовательность бесконечно большой?
14. Докажите, что сумма двух бесконечно малых последовательностей является бесконечно малой. Верно ли аналогичное утверждение для бесконечно больших последовательностей? Ответ обоснуйте.
15. Пусть 
- бесконечно малая последовательность. Следует ли отсюда, что 
и 
бесконечно малые последовательности. Ответ обоснуйте.
16. Пусть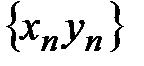 
- бесконечно малая последовательность. Следует ли отсюда, что хотя бы одна из последовательностей бесконечно малая? Ответ обоснуйте.
17. Сформулируйте на языке 
определение расходящейся последовательности и дайте геометрическую интерпретацию этого определения.
18. Пусть последовательность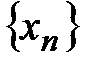 
сходится, а последовательность 
расходится. Докажите, что расходится, 
сходится, 
расходится при 
.Покажите на примерах, что последовательность 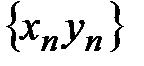может как сходиться, так и расходиться.
19. Сформулируйте: а) определение монотонной последовательности; б) признак сходимости монотонной последовательности.
20. Является ли ограниченность монотонной последовательности необходимым и достаточным условием сходимости: а) монотонной последовательности; б) произвольной последовательности?
21. Сформулируйте теорему Больцано-Вейерштрасса.
22. Верно ли утверждение: если последовательность неограниченая, то из нее можно выделить сходящуюся подпоследовательность?
23. Сформулируйте определения: а) фундаментальной последовательности; б) нефундаментальной последовательности.
24. Сформулируйте критерий Коши сходимости последовательности.
25. Какой предел называют числом e?
Числовые ряды
Примеры решения задач
Теоремы об арифметических операциях над числовыми последовательностями имеют очень большое как теоретическое, так и практическое значение. Но, несмотря на свою простоту, их правильное применение представ
|
|
|
