 |
Обработка результатов нескольких серий измерений одной и той же величины
|
|
|
|
Лабораторная работа №1
Определение погрешностей результатов измерений
Обработка результатов многократных измерений одной и той же величины.
Задание 1. При многократном измерении одной и той же физической величины Q получена серия из 24 результатов измерений Qi;  . Исключить ошибки из результатов измерений. Исходные данные:
. Исключить ошибки из результатов измерений. Исходные данные:
Таблица 1
| № измерения | Qi | № измерения | Qi | № измерения | Qi | № измерения | Qi |
Решение. 1). Определяем оценки результата измерения  и среднего квадратического отклонения
и среднего квадратического отклонения  по формулам:
по формулам:
 =
=  ,
, 
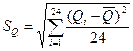 =
=  ,
,
и проверяем с помощью Microsoft Excel следующим образом: на листе Excel записываем столбцы 1 и 2 таблицы 1:
Таблица 2
| № | Qi | 
| 
|
| -1,9583 | 3,8351 | ||
| 1,0417 | 1,0851 | ||
| 2,0417 | 4,1684 | ||
| 2,0417 | 4,1684 | ||
| -0,9583 | 0,9184 | ||
| -0,9583 | 0,9184 | ||
| -0,9583 | 0,9184 | ||
| -0,9583 | 0,9184 | ||
| -2,9583 | 8,7517 | ||
| -3,9583 | 15,6684 | ||
| 8,0417 | 64,6684 | ||
| 2,0417 | 4,1684 | ||
| -0,9583 | 0,9184 | ||
| -0,9583 | 0,9184 | ||
| -0,9583 | 0,9184 | ||
| -0,9583 | 0,9184 | ||
| 0,0417 | 0,0017 | ||
| 0,0417 | 0,0017 | ||
| -0,9583 | 0,9184 | ||
| -1,9583 | 3,8351 | ||
| -2,9583 | 8,7517 | ||
| -2,9583 | 8,7517 | ||
| -0,9583 | 0,9184 | ||
| 11,0417 | 121,9184 | ||

| 483,9583 | ||

| 258,9582 |
а). Выделяем ячейку для искомого значения  (щелчком по левой кнопке), выбираем значок fx на панели инструментов, затем находим функцию Статистические - СРЗНАЧ в окне ниспадающего меню, нажимаем OK, в поле Число1 заносим столбец значений х с помощью мыши, нажимаем OK.
(щелчком по левой кнопке), выбираем значок fx на панели инструментов, затем находим функцию Статистические - СРЗНАЧ в окне ниспадающего меню, нажимаем OK, в поле Число1 заносим столбец значений х с помощью мыши, нажимаем OK.
|
|
|
b). Для удобства вычисления среднего квадратического отклонения результата измерения  добавим в таблицу столбцы 3 и 4. Для этого выделяем ячейку в строке рядом со значением Q1, в выделенной ячейке ставим знак “ = “, щелкаем мышью по ячейке, содержащей значение Q1, знак «-», щелкаем по ячейке, содержащей
добавим в таблицу столбцы 3 и 4. Для этого выделяем ячейку в строке рядом со значением Q1, в выделенной ячейке ставим знак “ = “, щелкаем мышью по ячейке, содержащей значение Q1, знак «-», щелкаем по ячейке, содержащей  , Enter. В строке формул выделяем знаком «$» букву номера ячейки, содержащей
, Enter. В строке формул выделяем знаком «$» букву номера ячейки, содержащей  , и протягивая мышью до последней строки, заполняемостальные ячейки третьего столбца.
, и протягивая мышью до последней строки, заполняемостальные ячейки третьего столбца.
Четвертый столбец заполняется по той же схеме: в выбранной ячейке ставим знак “ = “, щелкаем мышью по ячейке, содержащей значение Q1 -  , знак «*», щелкаем по ячейке, содержащей Q1 -
, знак «*», щелкаем по ячейке, содержащей Q1 -  , Enter. Протягивая мышью до последней строки, заполняемостальные ячейки четвертого столбца.
, Enter. Протягивая мышью до последней строки, заполняемостальные ячейки четвертого столбца.
с). Суммируем все значения (Qi -  )2 – содержимое ячеек четвертого столбца, используя значок ∑ (автосумма) на панели инструментов. Результат делим на 24 и используя значок fx на панели инструментов, находим функцию Математические – КОРЕНЬ, получаем:
)2 – содержимое ячеек четвертого столбца, используя значок ∑ (автосумма) на панели инструментов. Результат делим на 24 и используя значок fx на панели инструментов, находим функцию Математические – КОРЕНЬ, получаем:

2. Чтобы обнаружить и исключить ошибки результатов измерений:
– вычисляем наибольшее по абсолютному значению нормированное отклонение


– задаемся доверительной вероятностью P = 0,95 и из соответствующих таблиц с учетом q = 1 – P находим соответствующее ей теоретическое (табличное) значение  :
:

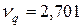 при n = 24;
при n = 24;
– сравниваем  и
и  :
:  . Это означает, что результат измерения Q24 является ошибочным, он должен быть отброшен.
. Это означает, что результат измерения Q24 является ошибочным, он должен быть отброшен.
Необходимо повторить вычисления согласно п.п. 1 и 2 для сокращенной серии результатов измерений и проводить их до тех пор, пока не будет выполняться условие  для всех результатов измерений.
для всех результатов измерений.
Повторяем вычисления, отбросив измерение №24. Получим согласно таблице 3:




Таблица 3
| № измерения | Qi | 
| 
|
| -1,4783 | 2,1853 | ||
| 1,5217 | 2,3157 | ||
| 2,5217 | 6,3592 | ||
| 2,5217 | 6,3592 | ||
| -0,4783 | 0,2287 | ||
| -0,4783 | 0,2287 | ||
| -0,4783 | 0,2287 | ||
| -0,4783 | 0,2287 | ||
| -2,4783 | 6,1418 | ||
| -3,4783 | 12,0983 | ||
| 8,5217 | 72,6200 | ||
| 2,5217 | 6,3592 | ||
| -0,4783 | 0,2287 | ||
| -0,4783 | 0,2287 | ||
| -0,4783 | 0,2287 | ||
| -0,4783 | 0,2287 | ||
| 0,5217 | 0,2722 | ||
| 0,5217 | 0,2722 | ||
| -0,4783 | 0,2287 | ||
| -1,4783 | 2,1853 | ||
| -2,4783 | 6,1418 | ||
| -2,4783 | 6,1418 | ||
| -0,4783 | 0,2287 | ||
| Σ | 131,7391 |
Имеем:
|
|
|

 при n = 23;
при n = 23;
Сравниваем  и
и  :
:  . Отбрасываем измерение №11 и повторяем вычисления. Для n = 22 аналогично получим:
. Отбрасываем измерение №11 и повторяем вычисления. Для n = 22 аналогично получим:

 ,
, 
 ,
,  ,
,  при n = 22;
при n = 22;
Сравниваем  и
и  . Так как
. Так как  , то результат измерения №10 не является ошибочным. Следовательно, окончательно остается 22 измерения, т.е. n = 22.
, то результат измерения №10 не является ошибочным. Следовательно, окончательно остается 22 измерения, т.е. n = 22.
Обработка результатов нескольких серий измерений одной и той же величины
Задание 2. При многократных измерениях одной и той же величины получены две серии по 12 результатов измерений в каждой. Эти результаты после внесения поправок представлены в таблице 5. Исключить ошибки из результатов измерений.
Исходные данные:
Таблица 4
| Серия 1 | Серия 2 | ||||||
| № измерения | Результат измерения | № измерения | Результат измерения | № измерения | Результат измерения | № измерения | Результат измерения |
Решение. 1). Обрабатываем экспериментальные данные по алгоритму, изложенному в п.п. 1,2 задания 1, при этом:
– определяем оценки результата измерения  и среднеквадратического отклонения
и среднеквадратического отклонения  ,
,
j = 1,2, используя таблицу 5 и этапы a) – c):
Таблица 5
| Серия 1 | Серия 2 | ||||||
| № из-мерения | Q1i | 
| 
| № из-мерения | Q2i | 
| 
|
| -2,1667 | 4,6944 | -0,7500 | 0,5625 | ||||
| 0,8333 | 0,6944 |  -0,7500 -0,7500
| 0,5625 | ||||
| 1,8333 | 3,3611 | -0,7500 | 0,5625 | ||||
| 1,8333 | 3,3611 | -0,7500 | 0,5625 | ||||
| -1,1667 | 1,3611 | 0,2500 | 0,0625 | ||||
| -1,1667 | 1,3611 | 0,2500 | 0,0625 | ||||
| -1,1667 | 1,3611 | -0,7500 | 0,5625 | ||||
| -1,1667 | 1,3611 | -1,7500 | 3,0625 | ||||
| -3,1667 | 10,0278 | -2,7500 | 7,5625 | ||||
| -4,1667 | 17,3611 | -2,7500 | 7,5625 | ||||
| 7,8333 | 61,3611 | -0,7500 | 0,5625 | ||||
| 1,8333 | 3,3611 | 11,2500 | 126,5625 | ||||
| Σ | 109,6667 | Σ | 148,2500 |

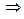
 ,
,  ;
;

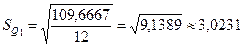 ,
,  ;
;
– обнаруживаем и исключаем ошибки:
|
|
|
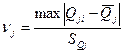
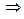
 ,
,  ;
;
 при n = 12;
при n = 12;
– сравниваем  и
и  с
с  :
:  и
и  . Результаты измерения Q 1,11 и Q 2,12 являются ошибочными, они должны быть отброшены.
. Результаты измерения Q 1,11 и Q 2,12 являются ошибочными, они должны быть отброшены.
Повторяем вычисления, при этом отбрасываем измерения 11 из серии №1 и 12 из серии №2 и используем таблицу 6:

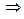
 ,
,  ;
;

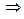
 ;
; 
Таблица 6
| Серия 1 | Серия 2 | ||||||
| № из-мерения | Q1i | 
| 
| № из-мерения | Q2i | 
| 
|
| -1,4545 | 2,1157 | 0,2727 | 0,0744 | ||||
| 1,5455 | 2,3884 | 0,2727 | 0,0744 | ||||
| 2,5455 | 6,4793 | 0,2727 | 0,0744 | ||||
| 2,5455 | 6,4793 | 0,2727 | 0,0744 | ||||
| -0,4545 | 0,2066 | 1,2727 | 1,6198 | ||||
| -0,4545 | 0,2066 | 1,2727 | 1,6198 | ||||
| -0,4545 | 0,2066 | 0,2727 | 0,0744 | ||||
| -0,4545 | 0,2066 | -0,7273 | 0,5289 | ||||
| -2,4545 | 6,0248 | -1,7273 | 2,9835 | ||||
| -3,4545 | 11,9339 | -1,7273 | 2,9835 | ||||
| 2,5455 | 6,4793 | 0,2727 | 0,0744 | ||||
| Σ | 42,7273 | Σ | 10,1818 |
 ;
;  ;
;
 при n = 11;
при n = 11;
Сравниваем  и
и  с
с  :
:  и
и  . Результаты измерений 10 из серии №1 и 9 из серии №2 не являются ошибочными и окончательно остается 11 измерений для обеих серий, т.е. n = 11.
. Результаты измерений 10 из серии №1 и 9 из серии №2 не являются ошибочными и окончательно остается 11 измерений для обеих серий, т.е. n = 11.
Считая результаты измерений распределенными нормально с вероятностью  ,
,
проверим значимость различия средних арифметических серий. Для этого:
– вычисляем моменты закона распределения разности:

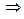
 , n 1 = n 2 = n
, n 1 = n 2 = n
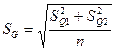
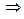

Задавшись доверительной вероятностью P = 0,95, определяем из таблицы интегральной функции нормированного нормального распределения Ф (t) значение t

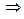 t = 1,645
t = 1,645
и сравниваем  с
с  , при
, при  :
:  <
<  . Различия между средними арифметическими в сериях с доверительной вероятностью P можно признать незначимыми.
. Различия между средними арифметическими в сериях с доверительной вероятностью P можно признать незначимыми.
3. Обрабатываем совместно результаты измерения обеих серий с учетом весовых коэффициентов:
1) определяем оценки результата измерения  и среднеквадратического отклонения S
и среднеквадратического отклонения S
 ,
,
 ,
,

 .
.
2) задавшись доверительной вероятностью P = 0,95, определяем по таблице t = 1,96 и доверительный интервал:
 ,
,
 ,
,
 .
.
Лабораторная работа №2
|
|
|


