 |
Проверка адекватности модели парной регрессии
|
|
|
|
Задание:
1. Вычислить коэффициент детерминации для полученной модели, используя различные формы представления коэффициента.
2. Проверить значимость коэффициента детерминации на основании F – теста.
Основная формула
Σ (yt - 
)2 = Σ (yэмп - )2 + Σ (yt-yэмп)2
или
TSS = ESS + RSS,
где TSS – полная сумма квадратов;
ESS - сумма квадратов, объясненная моделью;
RSS – остаточная сумма квадратов.
Ход работы
1). Находим эмпирическое значение yэмп величины y: выделяем ячейку, в выделенной ячейке ставим знак =, щелкаем мышью по ячейке, содержащей значение а, ставим в строке формул знак $ перед буквой и цифрой, чтобы зафиксировать значение, ставим знак +, щелкаем мышью по ячейке, содержащей значение b,снова ставим в верхней строке формулы знак $ перед буквой и перед цифрой, чтобы зафиксировать значение, нажимаем знак *, щелкаем мышью по ячейке, содержащей значение x, нажимаем Enter. Удерживая левую кнопку мыши, протягиваем вниз, чтобы получилось 15 ячеек. Нашли 15 значений yэмп, соответствующие значениям х.
2). Находим ESS: выделяем одну ячейку, в выделенной ячейке ставим знак «=», открываем скобку, щелкаем мышью по ячейке, содержащей первое значение yэмп, ставим знак «-», далее щелкаем мышью по ячейке, содержащей среднее значение 
, фиксируем его в строке формул знаком $ перед буквой и перед цифрой, закрываем скобку, и умножаем на аналогичную скобку, так как нам нужен её квадрат, нажимаем Enter. Удерживая левую кнопку мыши, протягиваем вниз еще на 14 ячеек. Затем находим сумму получившихся значений: щелкаем по ячейке, находящейся ниже этих значений, ставим знак =, выбираем значок ∑ (автосумма) на панели инструментов, и выделяем с помощью мыши все получившиеся значения произведений, нажимаем Enter.
|
|
|
3). Находим TSS: делаем все то же самое что и в пункте 2), только вычитаем среднее значение 
не от yэмп, а от y.
4). Находим RSS: выделяем 1 ячейку, в выделенной ячейке ставим знак «=», открываем скобку, щелкаем мышью по ячейке, содержащей первое значение y, ставим знак «-», далее щелкаем мышью по ячейке, содержащей значение yэмп, закрываем скобку и умножаем на аналогичную скобку, нажимаем Enter. Удерживая левую кнопку мыши, протягиваем вниз еще на 14 ячеек. Находим сумму получившихся значений: щелкаем по ячейке, находящейся ниже этих значений, ставим знак =, выбираем значок ∑ (автосумма) на панели инструментов, и выделяем с помощью мыши все получившиеся значения произведений, нажимаем Enter.
5). Находим коэффициент детерминации по первой формуле:
R2 = ESS/TSS.
Выделяем ячейку, ставим знак «=», щелкаем мышью по ячейке, содержащей значение суммы ESS, ставим знак «/», щелкаем мышью по ячейке, содержащей значение суммы TSS, нажимаем Enter.
6). Находим коэффициент детерминации по второй формуле:
R2 = 1- (RSS/TSS).
Выделяем ячейку, ставим знак «=»,нажимаем 1, ставим знак «-», затем открываем скобку, щелкаем мышью по ячейке, содержащей значение суммы RSS, ставим знак «/», щелкаем мышью по ячейке, содержащей значение суммы TSS, закрываем скобку, нажимаем Enter.
7). Находим коэффициент детерминации по третьей формуле:
R2 = r(y, yэмп )2,
где
r(y, yэмп )2 =cov(y, yэмп) / (var(y)*var(yэмп)),
cov(y, yэмп)= 1/(t-1)* Σ (y- )* (yэмп- 
).
Для этого выполняем промежуточные действия:
1). Находим аналогично из первого задания.
2). Находим сумму из формулы ковариации: выделяем ячейку, в выделенной ячейке ставим знак «=», открываем скобку, щелкаем мышью по ячейке, содержащей первое значение y, ставим знак «-», далее щелкаем мышью по ячейке, содержащей значение , фиксируем его в верхней строке формулы знаком $ перед буквой и перед цифрой, закрываем скобку, ставим знак «*», открываем скобку, щелкаем мышью по ячейке, содержащей первое значение yэмп, ставим знак «-», далее щелкаем мышью по ячейке, содержащей значение yэмп и фиксируем его в верхней строке формулы знаком $ перед буквой и перед цифрой, закрываем скобку, нажимаем Enter. Удерживая левую кнопку мыши, протягиваем вниз еще на 14 ячеек. Находим сумму получившихся значений: щелкаем по ячейке, находящейся ниже этих значений, ставим знак «=», выбираем значок ∑ (автосумма) на панели инструментов, и выделяем с помощью мыши все получившиеся значения произведений, нажимаем Enter.
|
|
|
3). Находим ковариацию. Выделяем ячейку, ставим знак «=», нажимаем 1, ставим знак «/» на клавиатуре набираем 14, [так как t =15, в формуле t -1], щелкаем мышью по ячейке, содержащей значение суммы из пункта 2), нажимаем Enter.
4). Находим var - дисперсию y и yэмп. Выделяем ячейку, ставим знак «=», выбираем значок fx на панели инструментов, затем находим ДИСП в окне меню, нажимаем OK, выделяем область по y, которая заносится в поле Число 1. Нажимаем OK. Аналогично находим дисперсию для величины yэмп.
5). Находим произведение дисперсий. Выделяем ячейку, ставим знак «=», щелкаем мышью по ячейке, содержащей значение дисперсии y, ставим знак «*», далее щелкаем мышью по ячейке, содержащей значение дисперсии yэмп, нажимаем Enter.
6). Извлекаем корень из произведения дисперсий. Выделяем ячейку, ставим знак «=», выбираем значок fx на панели инструментов, затем находим КОРЕНЬ в окне меню, нажимаем OK, выделяем ячейку со значением из пункта 5), которая заносится в поле. Нажимаем OK.
7). Находим коэффициент корреляции r. Выделяем ячейку, ставим знак «=», щелкаем мышью по ячейке, содержащей значение ковариации из пункта 3), ставим знак «/», далее щелкаем мышью по ячейке, содержащей значение корня из пункта 6), нажимаем Enter.
8). Находим коэффициент детерминации по третьей формуле. Выделяем ячейку, ставим знак «=», щелкаем мышью по ячейке, содержащей значение коэффициента корреляции r из пункта 7), ставим знак «*», и щелкаем по той же ячейке, нажимаем Enter.
8). Проверяем адекватность модели с помощью F - теста. Вычисляем значение F -критерия на основе формулы
F = R2/((1- R2)/(t-2)),
где t =15- число наблюдений.
|
|
|
Выделяем ячейку, ставим знак «=», щелкаем мышью по ячейке, содержащей значение коэффициента детерминации R2 из пункта 5), ставим знак «/», ставим скобки ((, затем 1, ставим знак «-», и щелкаем по той же ячейке R2, первую скобку закрываем, ставим знак «/», число 13, вторую скобку закрываем, нажимаем Enter.
9). Находим F табличное для уровней значимости 0,05 и 0,01.
Если F, полученное в пункте 8), больше F табличного для данного уровня значимости, то нулевая гипотеза H0 отклоняется на этом уровне значимости.
Варианты для парной регрессионной модели
Вариант № 1
| ||||||||||
| ||||||||||
|
Вариант № 2
|
| ||||||||||
|
| ||||||||||
|
|
Вариант № 3
|
| ||||||||||
|
| ||||||||||
|
|
Вариант № 4
|
| ||||||||||
|
| ||||||||||
|
|
Вариант № 5
|
| ||||||||||
|
| ||||||||||
|
|
Вариант № 6
|
| ||||||||||
|
| ||||||||||
|
|
Вариант № 7
|
| ||||||||||
|
| ||||||||||
|
|
Вариант № 8
|
| ||||||||||
|
| ||||||||||
|
|
Вариант № 9
|
| ||||||||||
|
| ||||||||||
|
|
|
|
|
Вариант № 10
|
| ||||||||||
|
| ||||||||||
|
|
Вариант № 11
|
| ||||||||||
|
| ||||||||||
|
|
Вариант № 12
|
| ||||||||||
|
| ||||||||||
|
|
Вариант № 13
|
| ||||||||||
|
| ||||||||||
|
|
Вариант № 14
|
| ||||||||||
|
| ||||||||||
|
|
Вариант № 15
|
| ||||||||||
|
| ||||||||||
|
|
Лабораторная работа №5
Задачи оптимизации
Планирование правовой, производственно-хозяйственной, управленческой и административной деятельности приводит к задачам, имеющим множество допустимых решений. Из этого множества решений нужно выбрать такое, которое бы оптимальным образом учитывало внутренние возможности и внешние условия для хозяйствующего или управляющего субъекта (выбор производственной программы, прикрепление к поставщикам, маршрутизация, раскрой материалов, приготовление смесей и т.д.).
Суть принципа оптимальности состоит в стремлении выбрать такое планово-управленческое решение 
, где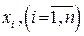 
– его компоненты, которое наилучшим образом учитывало бы внутренние возможности и внешние условия производственной деятельности хозяйствующего субъекта. С этой целью нужно выбрать некоторый критерий оптимальности экономического или правового показателя, позволяющего сравнивать эффективность тех или иных планово-управленческих решений («максимум прибыли», «минимум затрат»,
«максимум рентабельности» и т.д.). При этом выбор планово-управленческого решения осуществляется из некоторой области возможных (допустимых) решений D; эту область называют также областью определения задачи.
На практике принцип оптимальности в планировании и управлении означает решить экстремальную задачу об отыскании максимума или минимума функции
при ограничениях
Вектор называется допустимым решением, или планом задачи оптимального программирования, если он удовлетворяет системе ограничений. А то допустимое решение , которое доставляет максимум или минимум целевой функции , называется оптимальным планом (решением) задачи.
|
|
|
Программирование – это процесс распределения ресурсов.
Математическое программирование - это использование математических моделей и методов для решения проблем программирования.
Если целевая функция является линейной, а система ограничений на ресурсы представляет собой систему линейных взаимосвязей между переменными, то такая задача является задачей линейного программирования.
|
|
|
