 |
9. Критерии сравнения средних двух нормальных генеральных совокупностей. Сравнение двух средних нормальных генеральных совокупностей в R.
|
|
|
|
9. Критерии сравнения средних двух нормальных генеральных совокупностей. Сравнение двух средних нормальных генеральных совокупностей в R.
Эффективность очистных сооружений
Санэпидемстанцией города Казани были проведены измерения концентрации ртути в воде реки Волги выше и ниже места сброса с очистных сооружений (по 20 проб выше и ниже сброса).
Вопрос: Влияет ли сброс на концентрацию ртути? Уровень значимости 0. 05.
Исходные данные: колонка 15, 20.
Файлы: “3. txt” – данные 1, 2 колонок
х- выборка значений концентрации ртути выше места сброса
у- выборка значений концентрации ртути ниже места сброса
α =0, 05 – уровень значимости
Рассмотрим 2 гипотезы:
Н0: Mx=My – сброс не влияет на концентрацию ртути
Н1: Mx< My– сброс влияет, при этом концентрация ртути выше места сброса меньше концентрации ртути ниже места сброса
Для проверки гипотез используют критерий Стьюдента.
Ход работы:
1. Укажем путь к рабочей папке:
> setwd(" D: \\2019-2020\\02-707\\Novikova" ) или > setwd(" D: /2019-2020/02-707/Novikova" )
2. Читаем данные из текстового файла и выводим их на экран:
> mydata< -read. table(" 3. txt", header=TRUE, sep="; ", dec=". " )
> mydata
3. Найдем среднее для каждой из колонок:
> mean(mydata[, 1]) – среднее x
[1] 11. 02905
> mean(mydata[, 2])- среднее y
[1] 12. 52705
4. Найдем дисперсию для каждой из колонок:
> var(mydata[, 1]) – дисперсия x
[1] 39. 66387
> var(mydata[, 2]) – дисперсия y
[1] 26. 25756
5. Чтобы проверить основные гипотезы, сначала необходимо проверить доп. гипотезы о равенстве дисперсий:
Н’0: Dx=Dy
Н’1: Dx≠ Dy
> var. test(mydata[, 1], mydata[, 2], alternative=" two. sided" ), mydata[, 1]-x, mydata[, 2]-y
6. Сравним мат. ожидания по критерию Стьюдента:
> t. test(mydata[, 1], mydata[, 2], alternative=" less", var. equal=TRUE), mydata[, 1]-x, mydata[, 2]-y
|
|
|
10. Критерии для сравнения дисперсий нескольких нормальных генеральных совокупностей. Сравнение нескольких средних нормальных генеральных совокупностей в R.
Рассматриваются k нормальных генер. совокупностей:
X1 ∼ N(a1, σ 1)
. . .
Xk ∼ N(ak, σ k )
Задача: проверить гипотезу о равенстве двух дисперсий
H0: D1 = D2 =... = Dk
H1: не все равны
Критерий Бартлетта (ni - не все равны) (bartlett. test(значения, группы) или bartlett. test(list(X1, X2, ..., Xk )))
Критерий Кохрана (n1 = n2 =... = nk )
11. Критерии сравнения средних нескольких нормальных генеральных совокупностей. Дисперсионный анализ в R.
Чтобы проверить основные гипотезы, сначала необходимо проверить доп. гипотезы о равенстве дисперсий по критерию Фишера:
Н’0: Dx=Dy Это м. б. в случае, если измерения проведены по одной методике.
Н’1: Dx≠ Dy
> var. test(mydata[, 1], mydata[, 2], alternative=" two. sided" )
· Критерий Стьюдента: t. test(mydata[, 1], mydata[, 2], alternative=" less", var. equal=TRUE)
· Рассмотрим 2 гипотезы:
Н0: Mx=My – сброс не влияет на концентрацию ртути
Н1: Mx< My– сброс влияет, при этом концентрация ртути выше места сброса меньше концентрации ртути ниже места сброса
1)Генеральные совокупности распределены нормально, причем их дисперсии неизвестны, а объем выборок n и m мал (следовательно, нельзя получить хорошие оценки генеральных дисперсий). Если предположить, что генеральные дисперсии равны, то в качестве критерия для проверки нулевой гипотезы Но: М (Х) = М (Y) служит случайная величина, имеющая при справедливости нулевой гипотезы распределение Стьюдента с k = n + m – 2 степенями свободы. Наблюдаемое значение критерия вычисляется по формуле
Критическая область строится в зависимости от вида конкурирующей гипотезы.
а) Н1: М (Х) ≠ М (Y) – критическая область двусторонняя, задаваемая неравенством |T| > tдвуст. кр. , где tдвуст. кр. (α /2, k= n + m – 2) находится из таблицы критических точек распределения Стьюдента.
б) Н1: М (Х) > М (Y) – критическая область правосторонняя, определяемая условием T > tправ. кр. . Критическая точка вновь находится по таблице критических точек распределения Стьюдента. Tкр. =(α; k = n + m – 2)
|
|
|
в) Н1: М (Х) < М (Y) – критическая область левосторонняя, T < – t. Tкр. =(α; k = n + m – 2)
2) Разные дисперсии. Критерий Стьюдента с поправкой Уэлча.
t. test(mydata[, 1], mydata[, 2], alternative=" less", var. equal=FALSE, paired=TRUE)
1) Генеральные совокупности Х и Y распределены нормально, причем известны их дисперсии. Из этих генеральных совокупностей извлечены выборки объемов соответственно т и п, для которых найдены выборочные средние. При заданном уровне значимости α проверяется нулевая гипотеза о равенстве математических ожиданий генеральных совокупностей:
Но: М (Х) = М (Y).
Статистическим критерием для проверки этой гипотезы является нормированная нормально распределенная случайная величина
. Вид критической области зависит от типа конкурирующей гипотезы:
а) Н1: М (Х) ≠ М (Y) – критическая область двусторонняя, zкр определяется как аргумент функции Лапласа, при котором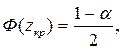 
и критическая область задается неравенством |Z| > zкр.
б) Н1: М (Х) > М (Y) – критическая область правосторонняя, zкр определяется как аргумент функции Лапласа, при котором 
и критическая область определяется неравенством Z > zкр.
в) Н1: М (Х) < М (Y) – критическая область левосторонняя, заданная неравенством Z < -zкр, где zкр вычисляется так же, как в предыдущем случае.
2) Имеются две независимые выборки большого объема, извлеченные из генеральных совокупностей, законы распределения и дисперсии которых неизвестны. При этом для объема выборки, не меньшего 30, можно считать, что выборочные средние распределены приближенно нормально, а выборочные дисперсии являются достаточно хорошими оценками генеральных дисперсий (следовательно, считаем известными приближенные значения генеральных дисперсий). Тогда задача сводится к предыдущей, и статистический критерий имеет вид:
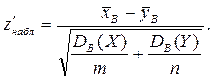
При этом выбор вида критической области и определение критических точек проводятся так же, как в пункте 1.
3) Генеральные совокупности распределены нормально, причем их дисперсии неизвестны, а объем выборок т и п мал (следовательно, нельзя получить хорошие оценки генеральных дисперсий). Если предположить, что генеральные дисперсии равны, то в качестве критерия для проверки нулевой гипотезы Но: М (Х) = М (Y) служит случайная величина,
|
|
|
,
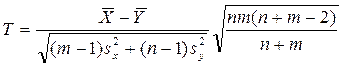имеющая при справедливости нулевой гипотезы распределение Стьюдента с k = n + m – 2 степенями свободы. Наблюдаемое значение критерия вычисляется по формуле
.
Критическая область строится в зависимости от вида конкурирующей гипотезы.
а) Н1: М (Х) ≠ М (Y) – критическая область двусторонняя, задаваемая неравенством |T| > tдвуст. кр. , где tдвуст. кр. (α /2, k) находится из таблицы критических точек распределения Стьюдента.
б) Н1: М (Х) > М (Y) – критическая область правосторонняя, где tкр. (α , k) определяемая условием T > tправ. кр. . Критическая точка вновь находится по таблице критических точек распределения Стьюдента.
в) Н1: М (Х) < М (Y) – критическая область левосторонняя, где tкр. (α , k). T < – tправ. кр. .
|
|
|
