 |
Дисперсионный анализ. Описание функции. anova(object). Параметры. Fнабл.=S2fact/S2ost, Fcrit=(a,k1=p-1,k2=pq-p). 12. Критерии для проверки гипотез (сравнение дисперсий) о генеральных совокупностях, которые не следуют нормальному закону распределения.
|
|
|
|
Дисперсионный анализ
Проверка гипотезы о равенстве мат. ожиданий. х1, х2, х3, …, хn – независимые с. в., распределенные нормально. На практике применяется ля установления влияния качественного фактора.
Рассмотрим 2 гипотезы:
Н0: M(x1)= M(x2)= M(x3) – фактор удаленности от дороги не влияет на концентрацию свинца
Н1: M(x1) ≠ M(x2) ≠ M(x3) – фактор удаленности от дороги влияет на концентрацию свинца
Описание функции
anova(object)
Параметры
object Объект класса lm, glm
Данный метод основан на разложении общей дисперсии численного признака на составляющие ее компоненты (отсюда и название метода ANalysis Of VAriance или ANOVA), сравнивая которые с друг другом посредством F-критерия Фишера можно определить, какую долю (по отношению к
совокупности случайных причин) общей вариации признака обуславливает действие на него известных величин (факторов). Метод основан на сравнении межгрупповой и внутригрупповой
изменчивости признака.
Fнабл. =S2fact/S2ost, Fcrit=(a, k1=p-1, k2=pq-p)
12. Критерии для проверки гипотез (сравнение дисперсий) о генеральных совокупностях, которые не следуют нормальному закону распределения.
А если данные не являются нормальными?
В этом случае применяют непараметрические тесты.
В отличие от параметрических тестов – непараметрические критерии (тесты) позволяют исследовать данные без каких-либо допущений о характере распределения переменных.
В непараметрических критериях обрабатываются не значения переменных, а их ранги или частоты. Ранг - это число, определяющее положение наблюдения в выборке отсортированных данных.
Непараметрические тесты можно применять при наличии в данных " выбросов" и неоднородных данных.
|
|
|
Тест Флигнера-Киллина - это непараметрический тест на однородность(равенство) групповых дисперсий на основе рангов.
Это полезно, когда данные распределяются ненормально или когда проблемы, связанные с выбросами в наборе данных, не могут быть решены.
Тест Флиннера-Киллина - один из многих тестов на однородность дисперсий, который наиболее устойчив к отклонениям от нормальности.
Для вычисления теста можно использовать функцию R fligner. test().
fligner. test(значения, группы)
Чтобы использовать функцию fligner. test() необходимо объединить два числовых вектора X и Y в одну переменную XX и добавить к этой переменной столбец Group, содержащий значения фактора, относящий значение переменной к определенной группе
fligner. test(XX, Group)
13. Критерии для проверки гипотез (сравнение медиан) о генеральных совокупностях, которые не следуют нормальному закону распределения.
При выборе критерия следует обратить внимание на две вещи: зависимость данных выборок друг от друга и объем выборок.
Независимые выборки (U-критерий Манна-Уитни)
wilcox. test(X, Y)
Зависимые (критерий Вилкоксона)
wilcox. test(X, Y, paired = T)
14. Корреляционный анализ (коэффициент корреляции и проверка гипотезы о его значимости, показатель ранговой корреляции). Корреляционный анализ в R.
Если при изменении одной с. в. меняется среднее значение (матожидание) другой, то такую зависимость называют корреляционной.
Примеры: 1)При увеличении удобрений, повышается сред. уровень урожаемости;
2)При увел-и уровня загазованности, повыш-ся уровень заболеваемости;
3)При увелич-и затрат на рекламу, повыщ-ся сред. уровень прибыли.
Корреляционный анализ - это проверка гипотез о связях между переменными с использованием коэффициентов корреляции.
Коэффициент корреляции
Коэффициент корреляции - это мера прямой или обратной пропорциональности между двумя переменными. Он чувствителен к связи только в том случае, если эта связь является монотонной, то есть не меняет направления по мере увеличения значений одной из переменных.
|
|
|
Обозначим коэффициент корреляции через г.
Свойства коэффициента корреляции:
1) 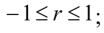
2) если X и Y - независимые случайные величины, то г = 0;
3) если r = 1 или г = -1, то данные равенства дают основание полагать, что между величинами имеет место быть зависимость;
4) если г > 0, то связь прямая (увеличение одного из исследуемых признаков (факторного) ведет к увеличению другого (результативного)), если г < 0, то связь обратная (увеличение одного из исследуемых признаков (факторного) ведет к уменьшению другого (результативного));
Коэффициент корреляции:
Все методы определения меры связи между случайными величинами делятся на параметрические и непараметрические. Параметрические включают в формулу расчета параметры распределения (коэффициент Пирсона, множественные коэффициенты корреляции), непараметрические - не включают в формулу для расчета параметры распределения и основаны на оперировании частотами и рангами (коэффициенты Фехнера, Спирмена, Кендалла).
Рассмотрим некоторые из перечисленных выше коэффициентов.
Числовой характеристикой тесноты линейной корреляционной связи двух переменных, измеренных в шкале интервалов или шкале отношений, является выборочный коэффициент корреляции Пирсона:
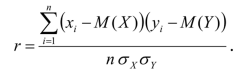
Формула для вычисления данного коэффициента корреляции содержит параметры м(х), м(у), ах, ау, поэтому данный метод определения меры связи является параметрическим. Также коэффициент Пирсона может быть вычислен в программе MS Excel с использованием стандартной функции «КОРРЕЛ». Подчеркнем еще раз, что коэффициент корреляции Пирсона есть мера прямолинейной взаимосвязи, он не чувствителен к криволинейным связям.
Достаточно ли этих данных, чтобы говорить о наличии зависимости м/у этими величинами? Другими словами, значимо ли выборочный коэф-т корр-и отличается от 0.
Проверка значимости выборочного коэф-та корреляции:
(х1, у1); (х2, у2); …(xn; yn) – парная выборка из 2х случайных величин Х и У.
Н0: r=0 – коэф-т кор-и =0
H1: r≠ 0 – коэф-т корр-и не равен 0
По критерию Стьюдента Тнабл. =r*(1/2*(n-2))/(1/2*(1-r2))
|
|
|
Ткр. =(а, k=n-2). |Tnabl|< Tcrit => H0 принимаем. Коэф-т корр-и не значим.
Теперь мы рассмотрим, как можно оценить корреляцию, обратившись непосредственно в среде R к функциям cor() и cor. test(). Различие между этими двумя функциями заключается в том, что cor() позволяет вычислить только сам коэффициент корреляции, тогда как cor. test() выполняет еще и оценку статистической значимости коэффициента, проверяя нулевую гипотезу о равенстве его
нулю. Естественно, предпочтительнее использовать именно вторую функцию.
Необходимо помнить, что коэффициент корреляции Пирсона основан на следующих важных допущениях:
° обе анализируемые переменные распределены нормально;
° связь между этими переменными линейна.
Для ненормально распределенных переменных, а также при наличии нелинейной связи между переменными, следует использовать непараметрический коэффициент корреляции Спирмена (англ. Spearman correlation coefficient). В отличие от коэффициента Пирсона, этот вариант коэффициента корреляции работает не с исходными значениями переменных, а с их рангами (однако формула при этом используется та же, что и для коэффициента Пирсона). Для вычисления коэффициента Спирмена в R при вызове функции cor. test() необходимо воспользоваться аргументом method со значением " spearman": cor. test (CAnumber, ZMlength, method = " spearman" ).
В качестве критериев оценки назависимости могут применяться и другие коэффициенты корреляции, например показатель ранговой корреляции Спирмена, позволяющий оценить нелинейную, но монотонную зависимость: в этом случае вычисляется кореляция не самих значений, а их рангов (порядковых номеров при упорядочении). Другим ранговым критерием
является τ -критерий Кендалла
|
|
|


