 |
Многолучевая интерференция
|
|
|
|
Допустим, что в некоторую точку экрана приходит N когерентных лучей с одинаковой интенсивностью. При этом фаза каждого последующего луча сдвинута относительно предыдущего на постоянную величину 
. Рассмотрим интерференционную картину, возникающую в этом случае.
Колебания,возбуждаемые лучами можно представить в виде экспонент:
………………………….. (1)
…………………………..
Результирующее колебание в точке наблюдения равно сумме колебаний (1):
(2)
Сумма в соотношении (2) представляет собой сумму N членов геометрической прогрессии с единичным первым членом, знаменателем 
и последним членом 
.
Известно, что сумма членов геометрической прогрессии определяется формулой:
(q – знаменатель прогрессии, b 1 и bn – первый и последний члены).
Поэтому результирующее колебание в (2) представим в виде:
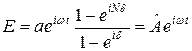, (3)
где 
– комплексная амплитуда результирующего колебания.
По определению комплексной амплитуды
,
где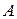 
- обычная амплитуда, а 
- начальная фаза.
Для нахождения квадрата амплитуды результирующего колебания (которому пропорциональна интенсивность света в данной точке) найдем произведение 
(комплексной амплитуды и комплексно сопряженной):
В соответствии с формулой Эйлера 
. Поэтому 
, а 
. Тогда
(4)
Каждый из лучей создает в точке наблюдения интенсивность, пропорциональную квадрату его амплитуды – 
(k – коэффициент пропорциональности). Тогда результирующая интенсивность 
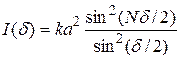. (5)
Из (5) видно, что при значениях
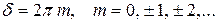(6)
дробь в соотношении (5) становится неопределенной. Значение дроби получим, взяв предел при 
. Воспользовавшись дважды правилом Лопиталя, получим:
. (7)
Следовательно, в точках экрана, где выполняется условие (6), для интенсивности света справедливо соотношение:
|
|
|
, (8)
а значит интенсивность в N2 раз больше по сравнению с интенсивностью от одного луча. Эти точки называются главными максимумами интерференционной картины, условие (6) – условием наблюдения главного максимума, число m называется порядком главного максимума.
Рассмотрим подробнее изменение интенсивности в промежутке между двумя главными максимумами.
В соотношении (5) 
при изменении m на единицу, т.е. при переходе к соседнему главному максимуму, d меняется на 2 p, а d/2 – на p. (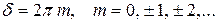). Следовательно, в промежутке между двумя главными максимумами знаменатель везде, кроме концов, конечен.
Представим, что 
плавно изменяется на p. Тогда аргумент синуса в числителе – N d /2 – изменяется на N p. При этом он проходит значения
N d/2 = p, 2 p,…(N - 1) p,
в которых числитель обращается в нуль. Всего таких значений имеется N – 1. Следовательно, в промежутке между соседними главными максимумами на экране располагается N - 1 минимум. Этим минимумам отвечает условие:
d = 
2p,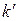 
=1, 2, 3, … N – 1.
Поскольку при плавном изменении d числитель изменяется периодически по закону синуса, а знаменатель при этом конечен, то в промежутках между минимумами естественно располагаются максимумы, которые называют вторичными. У вторичных максимумов, ближайших к главному интенсивность максимальна, вследствие того, что синус в знаменателе при приближении к краям рассматриваемого интервала изменения d уменьшается. Но, можно показать, что она не превышает 1/22 интенсивности главного максимума. Итоговая интерференционная картина имеет вид, показанный на рисунке.
Пунктиром на рисунке показано распределение интенсивности по экрану в случае двух источников – N = 2 (например, для двух щелей в опыте Юнга). Очевидно, что с ростом N главное максимумы сужаются. Действительно, первое нулевое значение синуса в числителе – 
– c ростом N наблюдается при меньшем 
. При этом интенсивность света в точках главных максимумов возрастает (
).
|
|
|
Рисунок 1.
Дифракционная решетка
Дифракционной решеткой (ДР) в простейшем случае называют совокупность одинаковых щелей, отстоящих на одинаковое расстояние друг от друга, как это показано на рисунке 2. Пусть b – ширина щели, а d – постоянная решетки (период пространственной повторяемости).
Допустим, что линза сверху освещается параллельным пучком света. После дифракции на щелях ДР лучи, идущие под углом φ к оптической оси линзы, собираются ею в точке наблюдения Р.
Лучи от одинаковых точек двух соседних щелей возбуждают в точке P колебания сдвинутые по фазе на некоторую величину , которая определяется оптической разностью хода 
между этими лучами. Поэтому и результирующие колебания от поверхностей двух соседних щелей будут сдвинуты по фазе на ту же величину . Поэтому результирующее колебание в точке Р является суммой колебаний с одинаковой амплитудой 
, сдвинутых по фазе друг относительно друга на одинаковую величину .
Сдвиг по фазе определяется постоянной решетки d, углом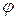 
и длиной волны 
используемого света:
. (9)
Таким образом, дифракционная решетка создает пучок лучей, очень похожий на рассмотренный нами случай многолучевой интерференции. Существенным отличием является тот факт, что интенсивность лучей идущих от щелей зависит от угла, который они составляют с оптической осью линзы.
Интенсивность результирующего колебания будет определяться формулой:
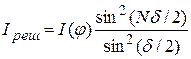, где (10)
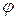– зависящая от угла функция, описывающая распределение света, идущего от одной щели в результате дифракции.
Для тех углов, для которых (в соответствии с (6)) d = d sin j 
= 2 
m,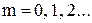 
наблюдаются главные максимумы. Условие их наблюдения можно представить в виде
, (11)
которое и называют условием наблюдения главного максимума ДР.
В тех направлениях, для которых
, (12)
= 0 в (10), и ни одна из щелей не посылает света.
Кроме этого между главными максимумами наблюдается N - 1 минимум, которым соответствует условие d sinj = 
, 
= 1, 2,… N - 1, N + 1,...,2 N - 1, 2 N + 1,…
Примерный вид распределения интенсивности света по экрану, создаваемый ДР, показан на рисунке 3. Подчеркнём, что пунктир на рисунке только качественно описывает распределение интенсивности по экрану от одной щели. При количественном построении график функции должен проходить намного ближе к оси абсцисс, поскольку интенсивность света одной щели намного меньше, чем в главных максиумах.
|
|
|
Отметим еще следующее. Поскольку 
, то количество наблюдающихся главных максимумов ДР, в соответствии с соотношением (11), не может быть более m 
d/l. В частности, если d/l < 2, то максимумов второго и более высоких порядков не наблюдается. Т.е. если постоянная ДР достаточно мала, то кроме нулевого порядка будут наблюдаться только максимумы первого порядка.
|
|
|
