 |
Интерференция в тонких пленках
|
|
|
|
26.1.  Интерференция света при отражении от тонких пластинок
Интерференция света при отражении от тонких пластинок
Путь на плоскопараллельную пластинку толщиной  с показателем преломления
с показателем преломления 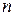 падает параллельный пучок света под углом
падает параллельный пучок света под углом  и отражается в точке
и отражается в точке  . Одновременно в точке
. Одновременно в точке  отражается и идет в том же направлении другой луч. Назовем эти лучи 1 и 2. Между отраженными лучами имеется оптическая разность xода:
отражается и идет в том же направлении другой луч. Назовем эти лучи 1 и 2. Между отраженными лучами имеется оптическая разность xода:
 (1)
(1)
Если она не превышает длины когерентности и расстояние АВ между лучами меньше радиуса пространственной когерентности, то при наложении отраженных лучей 1 и 2 должна наблюдаться их интерференция.
Из геометрических соображений следует:
 (2)
(2)
Поэтому оптическая разность хода 
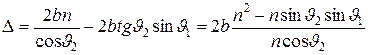 (2)
(2)
Но по закону отражения света  . Поэтому знаменатель
. Поэтому знаменатель

Тогда оптическая разность хода
 (3)
(3)
Учтем изменение фазы луча 1 при отражении в точке  – изменение фазы на
– изменение фазы на  эквивалентно увеличению разности хода на
эквивалентно увеличению разности хода на  :
:
 (4)
(4)
Для выполнения условия временной когерентности разность кода не должна превышать длину когерентности, а значит должно выполняться условие:

Выразим толщину пленки и получим условие, которому она должна удовлетворять, чтобы можно было наблюдать интерференцию лучей, отраженных от ее поверхностей:
 (5)
(5)
 в числителе можно пренебречь по сравнению с
в числителе можно пренебречь по сравнению с  . Корень в знаменателе имеет величину порядка единицы. Поэтому ориентировочно толщина пленки должна удовлетворять должна удовлетворять соотношению:
. Корень в знаменателе имеет величину порядка единицы. Поэтому ориентировочно толщина пленки должна удовлетворять должна удовлетворять соотношению:

Если для наблюдения интерференции использовать солнечный свет, то можно положить, что  . Человеческий глаз отличает оттенки цвета, отличающиеся по длине волны на
. Человеческий глаз отличает оттенки цвета, отличающиеся по длине волны на  . В этом случае интерференция наблюдаема при толщине пленки
. В этом случае интерференция наблюдаема при толщине пленки  . Именно по этой причине мы не наблюдаем интерференции при отражении света от поверхностей обыкновенного стекла.
. Именно по этой причине мы не наблюдаем интерференции при отражении света от поверхностей обыкновенного стекла.
|
|
|
Лучи 1 и 2 в падающем пучке отстоят на расстояние  = АВ. Из геометрических соображений следует, что
= АВ. Из геометрических соображений следует, что
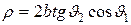
При угле падения порядка 
 можно положить
можно положить 
Радиус пространственной когерентности  солнечного света определяется угловым размером солнца, который составляет
солнечного света определяется угловым размером солнца, который составляет  рад. Поэтому
рад. Поэтому

 Поэтому, если мы хотим наблюдать интерференцию в солнечном свете при углах падения
Поэтому, если мы хотим наблюдать интерференцию в солнечном свете при углах падения  , необходимы пленки толщиной менее
, необходимы пленки толщиной менее 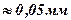 . Пленками такой и меньшей толщины растекаются по поверхности воды минеральные масла, и именно об этом свидетельствует радужная окраска поверхности воды в лужах.
. Пленками такой и меньшей толщины растекаются по поверхности воды минеральные масла, и именно об этом свидетельствует радужная окраска поверхности воды в лужах.
Полосы равного наклона
Пусть тонкая плоскопараллельная пластинка освещается рассеянным монохроматическим светом. Расположим параллельно пластинке собирающую линзу, в ее фокальной плоскости – экран. В рассеянном свете имеются лучи самых разнообразных направлений. Лучи, падающие под углом  , дают по 2 отраженных, которые соберутся в точке
, дают по 2 отраженных, которые соберутся в точке  . Это справедливо для всех лучей, падающих на поверхность пластинки под данным углом, во всех точках пластинки. Линза обеспечивает сведение всех таких лучей в одну точку, поскольку параллельные лучи, падающие на линзу под определенным углом, собираются ею в одной точке фокальной плоскости, т.е. на экране. В точке О птическая ось линзы пересекает экран. В этой точке собираются лучи, идущие параллельно оптической оси.
. Это справедливо для всех лучей, падающих на поверхность пластинки под данным углом, во всех точках пластинки. Линза обеспечивает сведение всех таких лучей в одну точку, поскольку параллельные лучи, падающие на линзу под определенным углом, собираются ею в одной точке фокальной плоскости, т.е. на экране. В точке О птическая ось линзы пересекает экран. В этой точке собираются лучи, идущие параллельно оптической оси.
Лучи, падающие под углом  , но не в плоскости рисунка, а в других плоскостях, соберутся в точках, расположенных на таком же расстоянии от точки
, но не в плоскости рисунка, а в других плоскостях, соберутся в точках, расположенных на таком же расстоянии от точки  , как и точка
, как и точка  . В результате интерференции этих лучей на некотором расстоянии от точки
. В результате интерференции этих лучей на некотором расстоянии от точки  образуется окружность с определенной интенсивностью падающего света. Лучи, падающие под другим углом, образуют на экране окружность с другой освещенностью, которая зависит от их оптической разности хода. В результате на экране образуются чередующиеся темные и светлые полосы в форме окружностей. Каждая из окружностей образована лучами, падающими под определенным углом, и они называются полосами равного наклона. Локализованы эти полосы в бесконечности.
образуется окружность с определенной интенсивностью падающего света. Лучи, падающие под другим углом, образуют на экране окружность с другой освещенностью, которая зависит от их оптической разности хода. В результате на экране образуются чередующиеся темные и светлые полосы в форме окружностей. Каждая из окружностей образована лучами, падающими под определенным углом, и они называются полосами равного наклона. Локализованы эти полосы в бесконечности.
|
|
|
Роль линзы может исполнять хрусталик, а экрана – сетчатка глаза. При этом глаз должен быть аккомодирован на бесконечность. В белом свете получаются разноцветные полосы.
Полосы равной толщины
Возьмем пластинку в виде клина. Пусть на нее падает параллельный пучок света. Рассмотрим лучи, отразившиеся от верхней и нижней граней пластинки. Если эти лучи свести линзой в точке  , то они будут интерферировать. При небольшом угле
, то они будут интерферировать. При небольшом угле  между гранями пластинки, разность хода лучей можно вычислять по форму
между гранями пластинки, разность хода лучей можно вычислять по форму  ле для плоскопараллельной пластинки. Лучи образовавшиеся от падения луча в некоторую другую точку пластинки соберутся линзой в точке
ле для плоскопараллельной пластинки. Лучи образовавшиеся от падения луча в некоторую другую точку пластинки соберутся линзой в точке  . Разность их хода определится толщиной пластинки в соответствующем месте. Можно доказать, что все точки типа Р лежат в одной плоскости, проходящей через вершину клина.
. Разность их хода определится толщиной пластинки в соответствующем месте. Можно доказать, что все точки типа Р лежат в одной плоскости, проходящей через вершину клина.
Если расположить экран так, чтобы он был сопряжен с поверхностью, в которой лежат точки P, Р1 Р2 то на нем возникнет система светлых и темных полос, каждая из которых образована за счет отражений от пластинки в местах определенной толщины. Поэтому в данном случае полосы называются полосами равной толщины.
При наблюдении в белом свете полосы будут окрашенными. Локализованы полосы равной толщины вблизи поверхности пластинки. При нормальном падении света – на поверхности.
В реальных условиях, при наблюдении окрашивания мыльных и масляных пленок наблюдается полосы смешанного типа.
|
|
|


