 |
Интерференция цилиндрических волн
|
|
|
|
Допустим, что имеются два когерентных источника 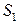 и
и 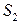 , которые совершают колебания в одной фазе и излучают когерентные волны. Расстояние от источников до экрана
, которые совершают колебания в одной фазе и излучают когерентные волны. Расстояние от источников до экрана 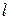 , между источниками
, между источниками 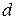 . На экране должна наблюдаться интерференционная картина.
. На экране должна наблюдаться интерференционная картина.
Рассчитаем оптическую разность хода лучей от источников до точки наблюдения  . Положение точки на экране будем характеризовать координатой
. Положение точки на экране будем характеризовать координатой 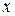 , отсчитываемой от точки О – проекции на экран середины отрезка между источниками. Свет от источника
, отсчитываемой от точки О – проекции на экран середины отрезка между источниками. Свет от источника 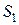 проходит расстояние
проходит расстояние 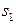 , от источника
, от источника 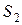 –
–  .
.  Из геометрических соображений можно записать следующие соотношения:
Из геометрических соображений можно записать следующие соотношения:
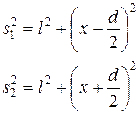 (24.21)
(24.21)
Вычтем левые и правые части и представим разность квадратов по известному алгебраическому соотношению:
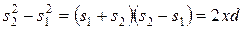 . (24.22)
. (24.22)
Будем считать, что в точках наблюдения выполняется соотношение:
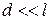 . (24.23)
. (24.23)
(Выполнение этого соотношения необходимо для того, чтобы интерференционная картина была различимой. Ниже мы это покажем.) Считая, что 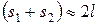 , получим, что разность
, получим, что разность 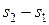 , равная оптической разности хода для источников в вакууме:
, равная оптической разности хода для источников в вакууме:
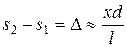 (24.24)
(24.24)
В среде с показателем преломления 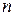
 . (24.25)
. (24.25)
Если в точке наблюдения выполняется условие
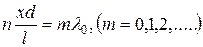 (24.26)
(24.26)
означающее, что оптическая разность хода равна целому числу волн в вакууме, то в точке наблюдения волны усиливают друг друга, и интенсивность света достигает максимального значения. Координаты таких точек получим, разрешив уравнение (24.26) относительно х:
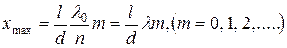 . (24.27)
. (24.27)
Соответственно в точках экрана, где выполняется условие
 (24.28)
(24.28)
означающее, что оптическая разность хода равна нечетному числу полуволн в вакууме, волны ослабляют друг друга, и интенсивность света достигает минимального значения. Координаты таких точек
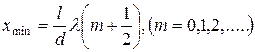 (24.29)
(24.29)
Картина, наблюдаемая на экране, если использовать свет с длиной волны, соответствующей красной части спектра, будет иметь вид:
|
|
|
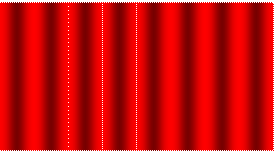
Если использовать голубой свет, то картина будет выглядеть немного иначе: у голубого света длина волны меньше, и соответственно полосы будут расположены гуще:
 |
Ширина полосы (расстояние между соседними максимумами)
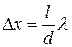 . (24.29)
. (24.29)
Очевидно, что условие 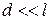 (24.23) необходимо для достижения полос шириной значительно больше длины волны света, а только такие полосы можно увидеть на экране.
(24.23) необходимо для достижения полос шириной значительно больше длины волны света, а только такие полосы можно увидеть на экране.
При использовании белого света в центре экрана будет светлая полоса, а по мере смещения из центра, в результате наложения интерференционных картин для различных длин волн, будет наблюдаться разложение света в спектр. Отметим, что ближе всего к центру картины будет наблюдаться максимум для фиолетовых волн (самых коротких из видимых), а потом максимумы для других цветов в соответствии с ростом длины волны.
Интерференция цилиндрических волн
КОГЕРЕНТНОСТЬ
Когерентность – согласованное протекание двух или нескольких волновых процессов. Абсолютной согласованности никогда не бывает, поэтому можно говорить о различной степени когерентности.
Различают временную и пространственную когерентность.
Временная когерентность
Уравнение реальных волн
Мы рассмотрели интерференцию волн, описываемых уравнениями вида:
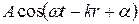 (1)
(1)
Однако такие волны являются математической абстракцией, поскольку волна, описываемая (1), должна быть бесконечной во времени и пространстве. Только в этом случае величины 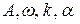 могут быть определенными константами.
могут быть определенными константами.
Реальная волна, образующаяся в результате наложения цугов от различных атомов, содержит в себе составляющие, частоты которых лежат в конечном диапазоне частот 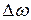 (соответственно волновые векторы в
(соответственно волновые векторы в 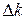 ), а А и a испытывают непрерывные хаотические изменения. Колебания, возбуждаемые в некоторой точке накладывающимися реальными волнами, можно описать выражением:
), а А и a испытывают непрерывные хаотические изменения. Колебания, возбуждаемые в некоторой точке накладывающимися реальными волнами, можно описать выражением:
|
|
|
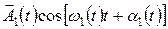
 и
и  (2)
(2)
Причем хаотические изменения функций от времени в (2) являются независимыми.
Для простоты анализа положим амплитуды волн постоянными и одинаковыми (экспериментально это условие реализуется достаточно просто):

Изменения частоты и фазы можно свести к изменениям только частоты или только фазы. Действительно, допустим, негармоничность функций (2) обусловлена скачками фазы. Но, по доказываемой в математике теореме Фурье, любую негармоническую функцию можно представить в виде суммы гармонических составляющих, частоты которых заключены в некоторых 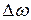 . В предельном случае сумма переходит в интеграл: любая конечная и интегрируемая функция
. В предельном случае сумма переходит в интеграл: любая конечная и интегрируемая функция 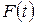 может быть представлена интегралом Фурье:
может быть представлена интегралом Фурье:
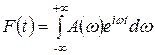 , (3)
, (3)
где  есть амплитуда гармонической составляющей частоты
есть амплитуда гармонической составляющей частоты 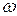 , аналитически определяемая соотношением:
, аналитически определяемая соотношением:
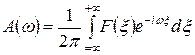 (4)
(4)
Итак, негармоническая вследствие изменения фазы функция представима в виде суперпозиции гармонических составляющих с частотами в некотором 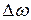 .
.
С другой стороны, функцию с переменной частотой и фазой можно свести к функции с переменной только фазой:
 (5)
(5)
Поэтому для укрощения дальнейшего анализа будем считать:

т. е. реализуем фазовый подход к понятию «Временная когерентность».
|
|
|


