 |
3.3. Определение химического состава сплава и соотношения фаз (или структурных составляющих)
|
|
|
|
3. 3. Определение химического состава сплава и соотношения фаз (или структурных составляющих)
На практике, используя правило отрезков, можно приближенно рассчитать химический состав сплава по соотношению основных структурных составляющих, определяемых при микроструктурном анализе. Например, требуется определить химический состав сплава системы свинец – сурьма (рис. 3. 3), если известно, что соотношение структурных составляющих (эвтектики и избыточной β -фазы) при температуре 20 оС равно 1: 2 или 33: 67 (в долевых %).
Определим на диаграмме концентрационную область существования искомого сплава Сх по его основным структурным составляющим эвтектике и β -фазе. Область с такими структурными составляющими расположена между точками Е и D, то есть 17, 3 < Сх< 98%. Затем при 20 оС проводим коноду, концы которой ограничиваются данными концентрациями. Строим схему рычага и, пользуясь правилом отрезков, запишем соотношение:
QЭ∙ EK= Qβ ∙ KD, или QЭ / Qβ = KD∙ EK
Находим длины отрезков через концентрации сплавов: KD=98% – Сх EK= Сх –17, 5%. Откуда QЭ / Qβ =98% – Сх / Сх –17, 5%=1/2 из условия задачи. Решая это равенство относительно Сх, получим состав сплава: ~71% Sb, остальное – Pb.
Для найденного состава сплава определим соотношение фаз α и β при 150 оС. Для этого проведем коноду через точку k´ до пересечения с ближайшими линиями на диаграмме (точки c´ и d´ ). Определяем химический состав фаз α (содержит 4% Sb, ост. Pb) и β (99% Sb, ост. Pb). Строим схему рычага и записываем соотношение Qα /Qβ = k´ d´ /c´ k´. Выражаем длины отрезков через концентрации сплавов, тогда Qα /Qβ = 99 –71(%) / 71– 4(%) = 28/67. В долевых процентах Qα и Qβ соответственно равны 29, 5 и 70, 5 %.
|
|
|
Правило отрезков можно применять для построения зависимости весовой доли какой-либо фазы от состава сплава при данной температуре или ее же от температуры для рассматриваемого сплава. На рис. 3. 4 приводится зависимость весовой доли фазы Al2Li от состава сплава Al - Li при 300 оС.
Графическое изображение такой зависимости дает возможность определить долю конкретной фазы в двухкомпонентной системе при определенной температуре.
На рис. 3. 5 построена температурная зависимость равновесного количества β -фазы системы Pb - Sb в сплаве с 60% Sb, остальное – Pb.

Рис. 3. 3. Зависимость весовой доли фазы Al2Li от состава сплава Al-Li при 300 оС.

Рис. 3. 5. Температурная зависимость равновесного количества β -фазы системы Pb–Sb в сплаве с 60 % Sb, остальное – Pb
Построение таких зависимостей позволяет для конкретного сплава определить соотношение фаз при любой температуре.
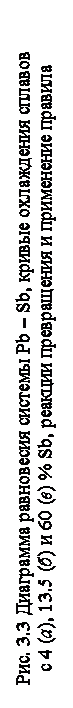

IV. ДИАГРАММЫ СОСТОЯНИЯ ТРЕХКОМПОНЕНТНЫХ СИСТЕМ
Пространственные диаграммы тройных сплавов сложны при рассмотрении процесса кристаллизации сплава. Поэтому для анализа процессов фазовых превращений используют построение изотермических и политермических разрезов, а также проекций изотерм и поверхностей ликвидуса и солидуса на плоскость концентрационного треугольника.
4. 1. Проекции поверхностей ликвидуса
В некоторых случаях большую информацию дают проекции поверхностей ликвидуса и солидуса. На рис. 4. 1 представлена проекция поверхностей ликвидуса и изотермы ликвидуса диаграммы состояния Pb–Bi–Sn с тройной эвтектикой.

Рис. 4. 1. Проекции изотерм и поверхностей ликвидуса трехкомпонентной системы Bi- Pb-Sn
Линии e1E, e2E и e3E – это проекции линий моновариантных трехфазных равновесий (Ж ↔ Ф1 + Ф2), показывающих изменение состава жидкой фазы при кристаллизации двойных эвтектик. Изменение состава жидкости и температуры следует по направлению стрелок. Проекции поверхностей ликвидуса показывают поля кристаллизации первичных фаз. В данном случае в областях I, II и III кристаллизация начинается с выделения Bi, Pb или Sn соответственно.
|
|
|
Три моновариантные кривые сходятся в одной точке четырехфазного равновесия, указывающей на состав жидкой фазы. Различают три варианта пересечения моновариантных кривых в нонвариантных точках (см. рис. 4. 2).

Рис. 4. 2. Пересечение моновариантых кривых фазовых равновесий в нонвариантных точках
Исходя из правила центра тяжести весового треугольника, можно записать реакции четырехфазного равновесия для указанных случаев:

| – эвтектическая; |

| – простая перитектическая; |

| – двойная перитектическая. |
В первом случае три кривые сходятся в одной точке, во втором – две кривые сходятся и одна выходит, причем с жидкостью взаимодействует фаза, находящаяся между сходящимися кривыми. В третьем случае – получающаяся твердая фаза располагается между расходящимися кривыми. Аналогичным правилам подчиняются монотектическая и монотектоидная, синтектическая и перитектоидная реакции четырехфазных равновесий.
Таким образом, проекции поверхностей ликвидуса образуют поля кристаллизации первичных фаз (I, II, III), обозначают точки нонвариантных превращений, соответствующие трехфазным равновесиям в двойных сплавах (е1, е2, е3), четырехфазным (Е) – в тройных сплавах, и показывают проекции моновариантных кривых трехфазных равновесий, соответствующих изменению состава жидких фаз, а также направление изменения состава и температуры. Проекции поверхностей солидуса, в свою очередь, указывают области существования одно-, двух- и трехфазных сплавов в твердом состоянии, а также на изменение состава твердых растворов. В данном случае проекцией поверхности солидуса будет треугольник АВС.
Проведем анализ проекций поверхностей ликвидуса диаграммы равновесия золото–теллур–висмут (рис. 4. 3).

Рис. 4. 3. Проекции поверхностей ликвидуса диаграммы Au – Te – Bi
На проекции диаграммы представлены восемь полей кристаллизации первичных фаз: 1) Bi; 2) Au; 3) AuTe2; 4) Te; 5) Bi2Te3; 6) Bi5Te3 и 7) Bi4Te.
|
|
|
На проекции также расположены пять эвтектических точек (e1–e5) трехфазных нонвариантных равновесий в двойных системах и три эвтектические точки (Е1, Е2 и Е3), соответствующие четырехфазным нонвариантным равновесиям. Приведем реакции эвтектических равновесий:
| 402 оС | 
|
| 383 оС | 
|
| 235 оС | 
|
Точки р1, р2 и р3 соответствуют перитектическим точкам нонвариантного превращения в двойных сплавах, а Р1, Р2 и Р3 – перитектическим точкам нонвариантного равновесия в тройных сплавах. Приведем температуры и реакции перитектических превращений:
| 456 оС | 
|
| 374 оС | 
|
| 346 оС | 
|
По этим реакциям можно проследить их написание по ранее изложенным правилам. Линии, соединяющие точки еi с Еi и Еi c Еi+n, отвечают трехфазному моновариантному эвтектическому равновесию (Ж ↔ Ф1 + Ф2), а линии, соединяющие точки еi c Рi, Ei с pi и pi с Рi – трехфазному моновариантному перитектическому равновесию (ЖРi + Ф1 ↔ Ф2). Проекция диаграммы имеет еще две характерные точки Sк1 и Sк2, лежащие на квазибинарных разрезах, называемые перевальными, по левую и правую стороны которых идет снижение температуры.
|
|
|


