 |
Метод регрессии с переключениями
|
|
Для выявления более корректной тенденции цены используем метод Регрессия с переключениями.
Регрессия с переключениями (регрессионные модели с переменным) наравне с адаптивным подходом является средством моделирования изменения структуры экономического процесса. Однако в отличие от адаптивного подхода здесь считается, что изменение структуры может происходить не в каждый момент времени.
В общем случае проблема построения регрессионной модели с переменной структурой включает решение следующих задач:
· Выявление точек перелома зависимостей (или их задание);
· Установление характера перехода (плавное или скачкообразное);
· Построение модели с переменной структурой;
· Проверка гипотезы о наличии структурных изменений.
Решение указанных задач представляет собой значительные трудности, а некоторые еще не имеют надежного формального решения. Однако при решении практических задач довольно часто встречаются ситуации, когда не требуется решение первых двух задач, поскольку априори можно сформулировать гипотезы о положении точек перелома и характере перехода. Например, при изучении во времени какого-либо экономического показателя предприятия (объем выпуска, себестоимость продукции и т.д.) заранее можно сказать, что в большинстве случаев переходы будут плавные, а точки перелома зависимости будут располагаться на временной оси в момент осуществления изменений условий производства (приватизация, изменение собственника, изменение технологии и т.д.). В ряде случаев, когда нет достаточно надежной априорной информации, местоположение точек перелома можно определить по графику экономического показателя от времени.
Поясним сущность регрессии с переключениями на примере. С этой целью рассмотрим рисунок 4.
Рисунок 4 – Пример регрессии с переключениями
На данном рисунке приведен скачкообразный переход от регрессии I к регрессии II. Непрерывный переход от регрессии I к регрессии III, изображенных пунктирной линией также приведен на рисунке 4.
На рисунке 4 штрихпунктирной линией показано изменение коэффициента регрессии на каждом шаге (адаптивный алгоритм) [13].
Использование априорной информации позволяет повысит точность оценивания параметров регрессии. Это важно при построении математических моделей экономических процессов, так как часто исходными данными являются короткие временные ряды. Предположим что область параметров задается в виде нечетких ограничений – равенств и неравенств. Рассматриваемая регрессия имеет вид
(17)
где 
- зависимая переменная, 
- параметр регрессии,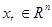 
– независимая переменная, 
- случайная величина, здесь и далее « / » означает транспонирование. Относительно регрессоров далее используется такое допущение
Допущение 1. Матрица 
невырождена
Лемма 1. Если выполняется допущение 1 и 
( 
- выпуклое множество), то 
строго монотонно возрастает, а 
строго монотонно убывает при 
, где 
Рассматриваемую задачу можно трактовать как задачу с двумя нечеткими целями выбора, так как с ростом r увеличивается первый критерий и уменьшается второй, и наоборот. Нечеткой i - целью, i = 1,2 , в множестве Z является некоторое его нечеткое подмножество, обозначим его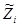 
. Функция принадлежности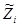
(18)
где 
.
Согласно лемме 1, 
уменьшается от 1 до 0, а 
увеличивается от 0 до 1.
Рассмотрим модель регрессии с переключением при одномерном переключателе, зависящем от времени t:
, (19)
где 
- n – мерный вектор регрессоров, 
- n – мерный вектор истинных значений параметров регрессии, 
- индекс точки переключения, 
- шум.
На отрезке времени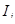 
с числом наблюдений 
параметры регрессии постоянны и равны 
. Пусть 
. Далее будем считать, что точки переключения 
известны, а величина 
может быть меньше n.
Пусть параметры регрессии на соседних отрезках It и It +1 достаточно близки, что можно сформулировать в виде нечеткого ограничения-равенства 
, где 
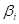– вектор, его компоненты – нечетко заданные числа, функции принадлежности которых сосредоточены в окрестности 0.
Расхождения, аналогичные приведенные в разделе 1, показывают, что задачу оценивания можно сформулировать как двухкритериальную.
(20)
(21)
где, 
, 
- выпуклое множество, 
и 
- весовые коэффициенты (известные величины). В частности, 
Введем следующие матрицы:
размерности mi x n;
X = diag (X(1), …, X(N)) размерности
;
Сформируем матрицу
.
Здесь r > 0 , 
,
где матрица 
имеет размерность
( N -1)xN .
Имеем 
где 
- вектор, размерность которого 
.
Причем 
.
Здесь 
где 
, 
.
Размерность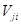 
равна 
. У вектора 
размерности 
компонента с индексом 
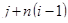равна 
, с индексом 
- равна 
, остальные компоненты нулевые.
Относительно регрессоров принимаем допущение
Допущение 6. У матрицы 
размерности 
столбцы линейно независимы.
Лемма 2. Пусть выполняется допущение 6, элементы матрицы 
.
Тогда матрица M имеет полный ранг.
Доказательство. Необходимое и достаточное условие линейной независимости векторов 
(существование полного ранга у M) – выполнение равенства
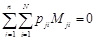(22)
для всех 
*.
Из (22) имеем две системы уравнений
, 
(23)
Количество уравнений в первой системе - 
, во второй - 
. Первую систему в развернутом виде можно представить как N систем уравнений
(24)
Вторую систему уравнений в (23) в развернутом виде представим так:
, (25)
где 
, 
- k-я компонента вектора .
Обратимся к первому уравнению в (25), коэффициенты которого 
, 
, 
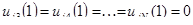. Отсюда следует 
.
Рассуждая аналогично, получим из остальных уравнение в (25)
(26)
Из этого соотношения и (24) получаем систему уравнений 
, где 
, 
. Согласно условию леммы, ее решение 
. Отсюда и из (26) следует 
. Лемма доказана.
Для определения оценок параметров регрессии с переключениями свернем два критерия в один.
Теорема 8. Если выполняются условия леммы 2, 
, где 
- выпуклое множество, то P - оценка параметров регрессии (19), соответствующая критериям (20), (21), является решением задачи
(27)
Доказательство. Квадратичный член функции цели 
имеет вид
Но M, согласно лемме 2, имеет полный ранг. Поэтому квадратичная форма 
положительно определена и, следовательно, (27) имеет единственное решение. Отсюда следует утверждение теоремы:
Можно показать, что свойства критериев такие же, что и приведенные в разделе 1. Поэтому единственная компромиссная P-оценка параметров регрессии с переключениями, соответствующая значению r = r*, может быть найдена по правилам, описанным в этом разделе, т.е. 
, функции 
определены в (18), 
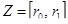. Здесь 
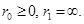[7, 14]
Описанный алгоритм оценивания реализован в пакете программ «ПРОГНОЗ».
Для нахождения коэффициентов регрессии и их среднеквадратических ошибок применяется пакет программ «ПРОГНОЗ».
Пакет программ «ПРОГНОЗ» предназначен для создания линейных по параметрам регрессионных моделей и моделей временных рядов с переменными или постоянными во времени параметрами. Полученные модели используются для многофакторного прогнозирования по уравнениям регрессии и однофакторного прогнозирования по модели временного ряда. Кроме того, пакет позволяет проводить предварительный анализ данных по выборке: оценивать математическое ожидание и дисперсию, взаимную корреляционную матрицу, проверять гипотезы о нормальном распределении генеральной совокупности.
Пакет ориентирован на персональные компьютеры (ПК) типа IBM PC XT/AT и совместимые с ними. Информация для расчетов находится в базе данных, создаваемой с помощью СУБД типа dBase, foxbase, Карат и т.п. БД состоит из двух файлов. Первый файл содержит числовые данные о переменных: каждое поле – одна переменная. Второй файл содержит справочник русских названий полей, а также название единицы отсчета данных (месяц, год, и т.п.).
Пакет «Прогноз» может быть использован для решения различных задач моделирования и прогнозирования. К ним относятся:
1) прогнозирование курса валют, акций, индексов цен различных товаров;
2) многофакторный прогноз себестоимости продукции;
3) определение норм расхода материалов и энергоносителей;
4) прогнозирование качества продукции по некоторым факторам (например, определение механического свойства металлопродукции по ее химическому составу);
5) анализ и прогнозирование инвестиционных процессов.
Регрессионная модель с переменными параметрами
Рассмотрим модель вида
, (4)
где t - номер наблюдений. В качестве регрессора zt используются линейные или нелинейные функции от исходных переменных xj , имеющихся в БД. Параметры в модели (4) могут меняться от наблюдения к наблюдению, либо быть постоянными на некоторых отрезках времени, задаваемых пользователем (регрессия с переключениями).
2.1. Параметры модели изменяются на каждом шаге. В этом случае используются два алгоритма. Первый алгоритм основан на постепенном забывании предыстории путем придания «старым» наблюдениям меньшего веса. Причем в течении некоторого периода времени веса всех наблюдений одинаковы, а от периода к периоду изменяются по показательному закону. Параметры регрессии в (4) оцениваются рекуррентно:
, t = 1, 2, …
,
где 
; 
; 
,
если t-е наблюдение – первое в 
-ом периоде постоянства весов, сt = 1 в противном случае.
Второй алгоритм оценивания параметров регрессии в (4) основан на трактовке задачи оценивании как двухкритериальной. Первый критерий –
,
второй критерий –
.
Искомая последовательность векторов 
находится в результате минимизации (2) где r определяется из условия, что первый критерий является главным.
Результаты решения: оценки параметров регрессии и среднеквадратические ошибки остатков выводятся в виде таблиц и графиков. Кроме того, вычисляются и выводятся сглаженные оценки указанных величин.
Сглаживание производится согласно соотношению
где 
- сглаженная оценка. Параметр 
задается пользователем.
Прогнозирование по одному временному ряду
Рассматривается модель с переменными параметрами 
(8)
где 
- последовательность независимых случайных величин, l – неизвестно. Параметры в (8) находятся двумя способами. Первый состоит в рекуррентном оценивании:
,
, (9)
где 
, 
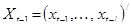, Ol - l-мерный вектор. Величины 
и l ( 
) выбираются такими, чтобы минимизировать ошибку прогноза на 1 шаг вперед на отрезке обучения [1, Т]:
,
где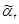 
находится по (9).
Другой способ определения параметров в (8) аналогичен определению параметров в (4) по второму алгоритму (см. р. 2.1). Отличие состоит в замене вектора zt в (5) на векторе Xt-1 [12].
Рисунок 5 – Общая схема построения регрессии в ПО «ПРОГНОЗ»