 |
Электростатическое поле в вакууме
|
|
|
|
Методические указания
К лабораторному практикуму с общим
Теоретическим введением
ЭЛЕКТРОСТАТИКА
312 – 8
МОСКВА 2007
Сборник методических указаний содержит описание лабораторных работ, относящихся к разделу «Электричество и магнетизм» типовой программы по физике для инженерно-технических специальностей высших учебных заведений.
Под редакцией проф. Н.П.Калашникова
Составитель проф. В.П.Красин
РИЦ МГИУ, 109280, Москва, Автозаводская, 16
СОДЕРЖАНИЕ
Теоретическое введение « Электростатика»
(проф. В.П. Красин)…………………………………….… …. 4
Лабораторная работа № 36
Изучение электростатического поля
(доц. А.Е. Горский, доц. В.В. Максименко)………………. 23
Лабораторная работа № 37
Изучение характеристик электростатического поля
(доц. А.Е. Горский),,………………………………………… 31
Лабораторная работа № 38
Определение ёмкости конденсатора
(проф. В.П.Красин)…………………………………………… 40
Лабораторная работа № 39
Измерение диэлектрической проницаемости
различных сред
(проф. В.П.Красин)…………………………………………… 49
Лабораторная работа № 40
Изучение процесса разряда конденсатора
(доц. И.Л. Галстян)…………………………………………… 56
Лабораторная работа № 41
Определение электроемкости конденсатора по осциллограмме его разряда через резистор
(доц. Г. Кучин)…………………………………………………63
ЭЛЕКТРОСТАТИКА
ВВЕДЕНИЕ
Современная жизнь немыслима без радио и телевидения, телефонов и телеграфа, всевозможных осветительных и нагревательных приборов, машин и устройств, в основе которых лежит возможность использования электрического тока.
Открытие электрического тока и всех последующих открытий, связанных с ним, можно отнести к концу XIX- началу XX веков. В это время по всей Европе и в том числе России прокатилась волна открытий, связанных с электричеством. Пошла цепная реакция, когда одно открытие открывало дорогу для последующих открытий на многие десятилетия вперёд.
|
|
|
Начинается внедрение электричества во все отрасли производства, появляются электрические двигатели, телефон, телеграф, радио, электронагревательные приборы, начинается изучение электромагнитных волн и влияние их на различные материалы, внедрение электричества в медицину.
Удивительный XIX век, заложивший основы научно-технической революции, так изменившей мир, начался с гальванического элемента - первой батарейки, химического источника тока (вольтова столба). Этим чрезвычайно важным изобретением итальянский учёный А. Вольта встретил новый 1800 год. Вольтов столб позволил вести систематическое изучение электрических токов и находить им практическое применение.
Над закладкой фундамента электродинамики трудилась целая плеяда ученых и изобретателей. Датчанин Х. Эрстед, француз А. Ампер, немцы Г. Ом и Г. Герц, англичане М. Фарадей и Дж. Максвелл, американцы Дж. Генри и Т. Эдисон.
Блестящие исследования в области электричества провел Ш. Кулон (14.06.1736 г. – 23.08.1806 г.) – французский физик и военный инженер. Исследовал и сконструировал в 1784 г. крутильные весы, с помощью которых в 1785 г. установил основной закон электростатики, а в 1788 г. распространил его на взаимодействия магнитных полюсов. Выдвинул гипотезу магнетизма, по которой магнитные жидкости не свободны, а связаны с отдельными молекулами, поляризующимися в процессе намагничивания. Сконструировал магнетометр (1785 г.).
К 60-м годам 19 века электродинамика благодаря работам Ф. Неймана, В.Вебера и Г. Гельмгольца считалась уже окончательно сформировавшейся наукой с четко определенными границами. Однако оригинальные идеи М. Фарадея заинтересовали Максвелла, и он задумал придать им математическую форму. Введя понятия токов смещения и напряженности поля, Максвелл сначала создал электродинамику диэлектриков, используя теорию О. Моссотти. Распространяя эти представления с поправками на магнетизм, он создает и теорию электромагнитной индукции. В итоге все построение сводится к знаменитым шести уравнениям Максвелла. Эти уравнения устанавливают непрерывность явлений, определяют изменения поля в отличие от ньютоновской модели, где законы определяют изменения поведения материальных частиц.
|
|
|
Целью настоящего теоретического введения является изучение основных положений электростатики, относящихся к разделам «Электростатическое поле и его характеристики» и «Проводники в электростатическом поле».
ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ И ЕГО ХАРАКТЕРИСТИКИ
Электростатическое поле в вакууме
Электростатическим полем называется поле, созданное любым неподвижным заряженным телом (в дальнейшем, для краткости, будем называть его зарядом).
Всякий заряд изменяет свойства окружающего его пространства, создает электрическое поле. Понятие поля является одним из фундаментальных, первичных понятий в физике.
Поле является формой материи, осуществляющей взаимодействие частиц вещества. Электростатическое поле определяется по действию силы на электрический заряд, помещенный в какую-либо точку поля. Следовательно, для того, чтобы выяснить, имеется ли в данном месте электростатическое поле, нужно поместить в данную точку заряд и установить, испытывает ли он действие силы или нет. По величине силы, действующей на данный заряд, можно судить об интенсивности поля.
Для обнаружения и исследования электрического поля нужно воспользоваться некоторым «пробным» зарядом. Исследуем с помощью точечного пробного заряда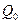 
поле, созданное точечным зарядом 
. Поместив пробный заряд в точку, положение которой относительно заряда определяется радиусом – вектором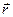 
, обнаружим, что на пробный заряд действует сила (в соответствии с законом Кулона):
. (1)
Из (1) следует, что сила, действующая на пробный заряд, зависит не только от величин, определяющих поле (
и 
), но и от величины пробного заряда 
. Из (1) видно, что 
для всех пробных зарядов зависит лишь от и . Поэтому принимают отношение в качестве величины, характеризующей электрическое поле:
|
|
|
. (2)
Векторную величину 
называют напряженностью электростатического поля в данной точке. В соответствии с (2) напряженность электростатического поля численно равна силе, действующей на единичный, точечный заряд, находящийся в данной точке поля. Направление вектора совпадает с направлением силы, действующей на положительный заряд.
Как следует из (1) и (2), напряженность поля точечного заряда пропорциональна величине заряда и обратно пропорциональна квадрату расстояния 
от заряда до данной точки поля:
. (3)
Вектор ориентирован вдоль прямой, проходящей через точку, в которой располагается заряд , и точку поля, в которой определяется напряженность. Причем, если заряд положителен, вектор направлен от заряда , если же отрицателен – к заряду.
За единицу напряженности электростатического поля принимается напряженность в такой точке, в которой на заряд, равный 1Кл, действует сила 1H. Эта единица имеет наименование вольт на метр (В/м).
Опыт показывает, что сила, с которой система зарядов действует на некоторый, не входящий в систему заряд, равна векторной сумме сил, с которыми действует на данный заряд каждый из зарядов системы в отдельности. Отсюда вытекает, что напряженность поля системы зарядов равна векторной сумме напряженностей полей, которые создавал бы каждый из зарядов системы в отдельности:
. (4)
Последнее утверждение носит название принципа суперпозиции (наложения) электростатических полей.
Принцип суперпозиции позволяет вычислять напряженность поля любой системы зарядов.
Электростатическое поле можно визуально представить с помощью силовых линий (или линий напряженности электростатического поля). Силовые линии проводят так, чтобы касательная к ним совпадала с направлением вектора . Густота линий выбирается так, чтобы количество линий, пронизывающих единицу поверхности перпендикулярной к линиям площадки, была равна численному значению вектора (рис. 1).
|
|
|
Рис. 1
Тогда по картине силовых линий напряженности можно судить о направлении и величине вектора в разных точках пространства. Рассмотрим поле, созданное положительным зарядом (рис. 2).
Рис. 2
Силовые линии поля, созданного положительным зарядом , представляют собой совокупность радиальных прямых, направленных от заряда.
Работа потенциальных сил при перемещении заряда по замкнутому пути равна нулю. Работа, совершаемая силами поля над зарядом при перемещении его по замкнутому контуру, может быть представлена следующим образом:
, (5)
где 
- проекция вектора на направление элементарного перемещения 
. (Кружок у знака интеграла означает, что интегрирование производится по замкнутому контуру).
Следовательно, 
,
выносим из-под знака интеграла и, т.к. 
получаем
(6)
Выражение 
называют циркуляцией вектора по контуру. Таким образом, для электростатических полей циркуляция вектора напряженности электростатического поля по любому замкнутому контуру равна нулю.
Из механики известно, что тело, находящееся в потенциальном поле сил, обладает потенциальной энергией, за счет которой совершается работа силами поля и, следовательно, работа может быть представлена как разность значений потенциальной энергии, которыми обладал заряд в точках 1 и 2 поля заряда 
:
.
Отсюда, для потенциальной энергии заряда в поле заряда получаем
.
Значение 
в выражении для потенциальной энергии обычно выбирается таким образом, чтобы при удалении заряда на бесконечность (
) потенциальная энергия обращалась в нуль. Тогда получаем 
, а формулу для потенциальной энергии можно записать в виде
. (7)
Воспользуемся зарядом 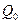в качестве пробного заряда для исследования поля. Как следует из (7), потенциальная энергия, которой обладает пробный заряд, зависит не только от его величины, но и от величин 
и 
, определяющих поле. Из (7) видно, что отношение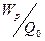 
не будет зависеть от величины пробного заряда .
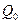. (8)
Величина 
называется потенциалом поля в данной точке и используется для описания электростатических полей. Потенциал численно равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки на бесконечность.
Подставляя в (8) значение потенциальной энергии (7), получаем для потенциала точечного заряда выражение
.
Потенциал поля, созданного системой зарядов в соответствии с принципом суперпозиции, равен алгебраической сумме потенциалов, созданных каждым зарядом в отдельности.
|
|
|
.
Вычисление потенциалов гораздо проще вычисления напряженности при наложении полей, т.к. напряженности складываются векторно, а потенциалы алгебраически.
Из (8) следует, что заряд , находящийся в точке поля с потенциалом , обладает потенциальной энергией.
. (9)
Следовательно, работа сил поля по перемещению заряда может быть выражена через разность потенциалов:
. (10)
Таким образом, работа, совершаемая над зарядом силами поля, равна произведению величин заряда на разность потенциалов в начальной и конечной точках. Если заряд точки с потенциалом удаляется на бесконечность (где по условию потенциал равен нулю), работа сил поля будет
. (11)
Из (11) следует, что потенциал численно равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки поля на бесконечность.
Единица потенциала – Вольт (В): 1B есть потенциал такой точки поля, в которой заряд в 1Кл обладает потенциальной энергией 1Дж.
Из всего сказанного следует, что электростатическое поле может быть описано как с помощью векторной величины , так и с помощью скалярной величины .
Определим связь между напряженностью и потенциалом электростатического поля. Если учесть, что пропорционально силе, действующей на заряд, а - потенциальной энергии заряда, легко сообразить, что связь должна быть аналогична связи между потенциальной энергией и силой.
Работа 
сил поля над зарядом на отрезке пути может быть представлена, с одной стороны, как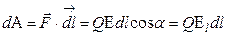 
, где - проекция вектора на направление , с другой стороны - как убыль потенциальной энергии заряда, т.е. как
Приравняв эти выражения, получим
,
откуда
,
где через 
обозначено произвольное направление в пространстве. В частности,
; 
; 
.
В общем случае:
.
Выражение, стоящее в скобках, называется градиентом скаляра (
), т.е.
(12)
Зависимость (12) отражает связь между напряженностью 
и потенциалом 
в общем случае.
Для наглядного изображения поля можно вместо силовых линий напряженности воспользоваться поверхностями равного потенциала или эквипотенциальными поверхностями. Если потенциал задан как функция координат 
, уравнение эквипотенциальной поверхности имеет вид:
.
Таким образом, эквипотенциальные поверхности - это геометрическое место точек с одинаковыми потенциалами.
Cиловые линии поля в любой точке ортогональны (перпендикулярны) эквипотенциальным поверхностям.
Эквипотенциальную поверхность можно провести через любую точку поля, следовательно, таких поверхностей можно провести бесконечное множество. Однако условились проводить поверхности таким образом, чтобы разность потенциалов 
для двух соседних поверхностей была всюду одна в та же. Тогда по густоте эквипотенциальных поверхностей можно судить о величине напряженности поля. Чем гуще располагаются эквипотенциальные поверхности, тем быстрее изменяется потенциал при перемещении вдоль нормали к поверхности. Следовательно, тем больше в этом месте , а значит и .
На рис. 3 и 4 приведены общие картины расположения силовых (сплошные) линий и эквипотенциальных (пунктирные) линий поверхностей для двух случаев; рис. 3 - изолированный (удаленный от всех) отрицательный заряд, рис. 6 - диполь.
Рис. 3 Рис. 4
Вычисление напряженности поля системы электрических зарядов можно значительно упростить, используя выведенную немецким математиком К. Гауссом (1777-1855) теорему, определяющую поток вектора электрического поля через произвольную замкнутую поверхность.
Поток вектора напряженности электрического поля через произвольную поверхность S, помещенную в неоднородное поле,
или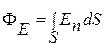 
,
где a — угол между вектором напряженности и нормалью 
к элементу поверхности; d S — площадь элемента поверхности; En — проекция вектора напряженности на нормаль.
Поток вектора напряженности через замкнутую поверхность
,
где интегрирование ведется по всей поверхности. В дальнейшем под понимаются векторы внешних нормалей, т. е. направленные вовне из области, ограниченной этой поверхностью.
Теорема Остроградского — Гаусса. Поток вектора напряженности через любую замкнутую поверхность, охватывающую заряды Ql, Q2,..., Qn,
Где 
— алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности; N — число зарядов.
|
|
|
