 |
Параллельное соединение конденсаторов
|
|
|
|
Батарея параллельно соединенных конденсаторов представлена на рис. 6.
Рис. 6
Так как одноименные обкладки соединены проводниками, а проводник является эквипотенциальным телом, то потенциалы всех одноименных обкладок равны между собой, то есть
. (18)
Из рис. 6.а видно, что общий заряд на батарее равен сумме зарядов на каждом из конденсаторов:
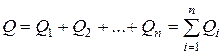. (19)
Подставляя в уравнение (19) формулу (14) и учитывая соотношение (18), получим формулу, определяющую общую ёмкость батареи конденсаторов, соединенных параллельно:
. (20)
Из формулы (20) видно, что если, например, соединено 
одинаковых конденсаторов ёмкостью 
каждый, то 
.
Параллельное соединение конденсаторов дает возможность:
а) увеличить ёмкость;
б) увеличить запасаемую энергию.
3.5. Заряд конденсатора
Большую роль в электрических цепях играют процессы заряда и разряда конденсаторов.
Рассмотрим процесс заряда конденсатора ёмкостью , включенного последовательно с резистором, обладающим сопротивлением 
(рис. 7,а). В исходном состоянии конденсатор разряжен, ключ разомкнут, на клеммах напряжение 
.
а) б)
Рис. 7
При замыкании ключа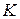 
в момент времени 
в цепи пойдет ток заряда конденсатора 
. Сумма падения напряжения на резисторе и напряжения на конденсаторе равна напряжению на клеммах 1, 2 
:
.
Учитывая законы Ома для участков цепи 
и определение электроёмкости (14), это выражение можно записать в виде
,
где Q = UcC - заряд на конденсаторе. Далее, учитывая определение силы тока 
, получим:
.
После преобразований имеем
.
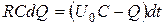Заменив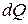 
на 
, получим 
. Интегрируя это уравнение, получим
, где 
- постоянная интегрирования.
После потенцирования получаем 
.
Из начальных условий: при , 
, 
, то есть 
, где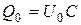 
- максимальный заряд на конденсаторе.
|
|
|
Учитывая, что 
, получим выражение, определяющее напряжение на обкладках конденсатора при заряде как функцию времени:
или, введя обозначение
, (21)
получим
Вид этой зависимости представлен на рис. 7,б.
3.6. Разряд конденсатора
Рассмотрим процесс разряда конденсатора ёмкостью через резистор, обладающий сопротивлением (рис. 8,а). В исходном состоянии конденсатор заряжен до напряжения 
, ключ разомкнут.
а) б)
Рис. 8
При замыкании ключа 
в момент времени в цепи пойдет ток разряда конденсатора 
. Так как ЭДС в цепи равна нулю, то по закону Ома в каждый момент времени
,
где 
- мгновенное значение падения напряжения на резисторе.
Учитывая, что , , 
, получим
или
.
Интегрируя эти уравнения, получим
, где 
- постоянная интегрирования.
Далее имеем:
.
Так как 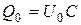при 
, то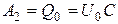 
, то есть 
, где 
- заряд на конденсаторе в момент начала разряда 
.
Учитывая, что 
, получим выражение, определяющее напряжение на обкладках конденсатора при его разряде как функцию времени:
(22)
или, учитывая соотношение (21),
Вид этой зависимости представлен на рис. 8,б.
Проанализируем выражение (22). В момент времени 
напряжение на конденсаторе 
, то есть численно равно времени, в течение которого напряжение на обкладках конденсатора при разряде уменьшается в 
раз (см. рис. 8,б).
При разряде потенциальная энергия электрического поля, накопленная в конденсаторе в процессе заряда, расходуется на поддержание в цепи электрического тока.
Для определения ёмкости в данной работе используется процесс разряда конденсатора (рис. 8,б), описываемый формулой (22). Пусть конденсатор неизвестной ёмкости С разряжается через резистор, обладающий сопротивлением R. Этот процесс описывается уравнением
,
из которого после логарифмирования получим
. (23)
Формула (23) используется для расчета ёмкости конденсатора.
Литература
Калашников Н.П., Смондырев М.А. Основы физики, т.1. Гл. 10, 11. М.: Дрофа, 2003.
|
|
|
Лабораторная работа №36
ИЗУЧЕНИЕ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Цель лабораторной работы
Целью лабораторной работы является изучение законов электростатики и экспериментальное исследование электростатического поля в простейших случаях.
|
|
|
