 |
Корреляционно-регрессионный анализ
|
|
|
|
Любой закон природы или общественное явление могут быть выражены в виде описания взаимосвязей, существующих между показателями этого закона или явления. При анализе характеристик инновационного проекта изучаются связи между его показателями, часть из которых является случайными величинами. Корреляционно-регрессионные модели базируются на том, что существует ряд факторов, влияющих на данную экономическую характеристику, например, величина инвестиций в инновационный проект влияет на величину чистой прибыли, которая будет получена от этого проекта.
Задача измерения связи между переменными решается на эмпирическом материале, представляющем собой выборку объема n из (k + 1)-мерной совокупности наблюдений или матрицы размером (k + 1)n (таблица 4).
Если количество независимых переменных больше двух, то исследуемая модель называется многофакторной. В таблице 4 представлена k-факторная модель.
Постановка задачи начинается с предварительного теоретического исследования инновационного проекта. Устанавливаются объект и задача исследования, формулируются теоретические гипотезы о наличии причинно-следственных связей. Затем приступают к сбору исходных данных, т.е. формируют выборку. Выборка должна быть репрезентативной — достаточной для того, чтобы по ее характеристикам судить о генеральной совокупности.
Как правило, исследуемые экономические процессы зависят от множества факторов. Включение в модель всех факторов приведет к ее неоправданному усложнению. Поэтому в модель включаются те факторы, которые охватывают наиболее существенные причинно-следственные связи. Обычно отсев слабо влияющих на исследуемый показатель факторов осуществляется в ходе построения многофакторной модели путем многошагового анализа. Вначале строится уравнение регрессии с максимально возможным количеством факторов. Затем с помощью определенных критериев, например t - критерия Стьюдента, исключаются факторы, оказывающие несущественное влияние на исследуемый параметр. На каждом шаге отсеивается по одному фактору. Отсеивание проводится до тех пор, пока в модели не останутся только значимые факторы.
|
|
|
Таблица 4
K – факторная модель
| Номер наблюдения | Переменные | |||||
| y | x1 | … | xj | … | xk | |
| y1 | x11 | … | x1j | … | x1k | |
| y2 | x21 | … | x2j | … | x2k | |
| … | … | … | … | … | … | … |
| i | yi | xi1 | … | xij | … | xik |
| … | … | … | … | … | … | … |
| n | yn | xn1 | … | xnj | … | xnk |
Метод «Монте-Карло»
Впервые описание метода «Монте-Карло» появилось в 1949 г. Название методу дал известный своими казино город Монте-Карло в княжестве Монако, так как именно рулетка является простейшим механическим прибором по реализации процесса получения случайных чисел, используемых в данном методе. При использовании метода строится математическая модель результирующего показателя инновационного проекта как функции от переменных и параметров. Под переменными понимаются величины, которые будут изменяться в процессе компьютерного эксперимента. Параметры — это величины, не изменяющиеся во времени.
На основе этой модели на электронной вычислительной машине проводятся имитационные эксперименты. При этом в каждом эксперименте результирующий показатель рассчитывается для значений переменных, выбираемых случайным образом за счет генерирования случайных чисел. Результаты всех имитационных экспериментов объединяются в выборку и анализируются с помощью статистических методов в целях получения закона распределения результирующего показателя. В отдельных случаях закон распределения не определяют, а ограничиваются моментами, характеризующими статистические параметры объекта.
|
|
|
Для анализа имитационных моделей обычно используются современные электронные вычислительные машины, поскольку расчеты являются достаточно трудоемкими и их количество велико.
Алгоритм определения закона распределения интересующего показателя или моментов этого распределения сводится к следующему:
1. Строится математическая модель результирующего показателя как функции от переменных и параметров.
2. Проводится анализ выбранных переменных. Из их числа выбираются только те, изменение которых существенно влияет на результат. Для этих целей можно, например, провести анализ чувствительности исследуемого основного показателя от различных факторов и выбрать из них те, к которым этот показатель наиболее чувствителен.
3. Определяются законы распределения выбранных переменных и корреляционные связи между ними.
4. Проводится компьютерный эксперимент, состоящий из заданного количества опытов. Это количество должно быть достаточным для построения репрезентативной модели.
4.1.для каждого опыта генерируются случайные числа, являющиеся реализацией каждой случайной переменной;
4.2.для полученных случайных чисел рассчитывают результирующий показатель и получают выборку, имеющую количество результирующих показателей, равное количеству опытов;
4.3.проводят статистический анализ выборки на предмет определения закона распределения результирующего показателя или для определения моментов этого распределения.
Метод «Монте-Карло» может быть применим к любому выходному показателю инновационного проекта. К таким показателям могут относиться, например, чистый приведенный доход, индекс прибыльности, внутренняя норма доходности и т.д.
Анализ безубыточности
Анализ безубыточности представляет собой расчет и анализ объема реализации, необходимого для возмещения всех издержек. Точка безубыточности представляет собой критический объем реализации товара (услуг), при котором совокупные доходы равны сумме всех издержек. Другими словами, точка безубыточности характеризует объем продаж, при котором выручка от реализации продукции совпадает с издержками производства. Смысл точки безубыточности поясняется на рисунке 4.
|
|
|
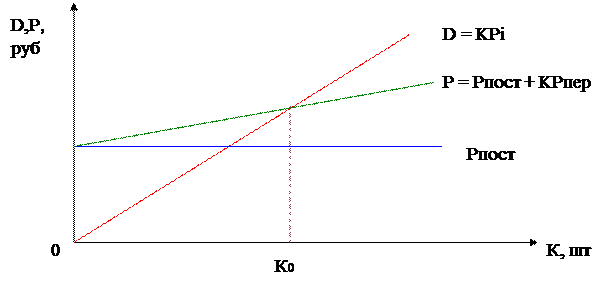
Рисунок 4 Точка безубыточности
Рпост – постоянные издержки, которые не изменяются при изменении объемов производства; P = Pпост + KPпер - совокупные расходы, состоящие из постоянных издержек и переменных издержек, изменяющихся пропорционально объему производства; Рпер – переменные издержки на единицу продукции; К - количество единиц продукции; D = KPi – совокупные расходы; Pi – цена единицы продукции.
Точка безубыточности К0 определяется равенством совокупных расходов и совокупных доходов D = P или K0P1 = Pпост + K0Pпер. Отсюда находим
Рпост
 К0 =.
К0 =.
Р1 - Рпер
Эта формула позволяет найти количество реализованного товара, при котором совокупные доходы равны сумме всех издержек. Чем ниже точка безубыточности, тем устойчивее эффект.
Анализ чувствительности
Прежде чем переходить к исследованию чувствительности проекта к различным показателям, введем понятие «эластичность». Понятие «эластичность функции» тесно связано с дифференцированием функции.
Эластичностью функции - называется предел отношения относительного приращения функции к относительному приращению переменной при стремлении приращения переменной к нулю.
Используя понятие «эластичность», определение чувствительности инновационного проекта можно сформулировать следующим образом: чувствительность инновационного проекта показывает, на сколько процентов изменится основной показатель этого проекта при изменении заданного параметра на один процент. Для проведения анализа чувствительности используется следующий алгоритм.
1. Выбирают основной показатель проекта (например, чистый
приведенный доход, внутреннюю норму доходности и т.д.).
2. Выбирают факторы, наиболее существенно влияющие на чувствительность (например, цена реализации, объем продаж, плата за кредит, сумма инвестиционных затрат, стоимость привлекаемого капитала и т.д.).
3. Рассчитывают значение основного показателя для заданных диапазонов выбранных факторов.
|
|
|
4. Определяют факторы, к которым проект наиболее чувствителен, и рассчитывают чувствительность.
5. По величине чувствительности проекта принимают решение о реализации проекта или о доработке технико-экономического обоснования.
Обычно доработку проекта проводят в целях снижения чувствительности. Это связано с тем, что при высоком значении чувствительности к изменению какого-либо фактора незначительное изменение этого фактора может привести к состоянию, при котором проект будет убыточным.
|
|
|


