 |
Порядок определения оптимальной партии заказа.
|
|
|
|
Расчёт минимальных совокупных издержек хранения запасов и порядок организации заказы сырья и материалов.
Важнейшим этапом управления запасами сырья и материалов, вошедших по методу ABC в группу A и частично в группу В, является определение оптимальной партии заказа.
В западной теории и практике для этих целей обычно применяется модель EOQ – модель Уилсона. Цель определения оптимальной партии заказа состоит в обеспечении запасами, необходимыми для поддержания производственного процесса при минимальных совокупных издержках хранения и организации заказа.
Идея модели Уилсона – это разделение затрат на:
ü расходы по хранению запасов (переменные);
ü расходы по организации заказов (условно постоянные).
Предположим,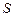 
– это годовой объём продаж; 
– годовое число заказов; 
– заказываемое количество товара потребителем. Тогда: 
.
Уровень запасов будет колебаться от величины Q после поступления заказа до нуля (или страхового запаса) накануне следующего поступления заказа.
При расчёте потребности в оборотных средствах обычно учитывается средняя стоимость запасов (M). Её можно определить:
(1), где:
– средняя величина запасов;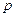 
– это цена единицы сырья или материала.
(2)
При расчёте издержек хранения учитываются затраты на аренду складов, амортизацию помещений, коммунальные услуги, охрану, страхование, потери от уценки (счёт 14), порчи, устаревание и другие затраты. Иногда эти издержки в виде стоимости денег на хранение трактуют как издержки упущенных возможностей.
Пусть все издержки хранения обозначим за C – это величина может быть приблизительная, и высокая точность расчётов вряд ли вообще возможна; с – это затраты по хранению единицы запаса (будем считать условно, что это некий норматив).
|
|
|
Теперь определим общую сумму издержек хранения (TCC). Она будет равна:
TCC=c*p*A
TCC, как правило, переменны, но стоимость организации каждого заказа принято считать постоянной (переписка, телефон-факс, представительские, командировочные расходы).
Пусть постоянные издержки равны F. И если размещается N заказов в год, то общая стоимость организации заказов (TOC) определяется:
(4)
Тогда: TCC=c*P*A=c*p*Q:2 (3)
N=S:2A
Из данной формулы видно, что число заказов снижается с ростом объёмов партии. Если сами заказы велики, их число в течение года мало, то малы и издержки организации заказов. Подставляя N в 4 формулу, мы можем определить TOC следующим образом:
TOC=FS:2A=FS:Q (5)
Общие совокупные издержки хранения и организация заказов (TIC) будут равны:
TIS=C*p*Q:2=F*S:Q (6)
Это формула служит основой для определения оптимальной партии заказа. Она позволяет найти компромисс между издержками, которые растут, и издержками, которые снижаются.
Приравнивание производной к нулю позволяет найти минимум издержек:
Отсюда: EOQ=кор кв из 2FS:CP
Это выражение и называется моделью Уилсона.
Как должна изменяться оптимальная величина заказа
при изменении объёма продаж?
При увеличении объёма расхода материалов оптимальный размер заказа растёт непропорционально изменению объёма расхода.
Главный вывод модели Уилсона – оптимальный размер заказа и средний размер запасов увеличиваются не пропорционально объёму продаж, а на множитель, равный корню квадратному из темпов роста объёма продаж. Отношение запасов к объёму продаж будет снижаться по мере роста объёмов продаж.
В каких случаях целесообразно использовать модель Уилсона
и какие ограничения имеет эта модель?
Данная модель даёт важные практические ориентиры для расчёта оптимальной партии заказа. В то же время она верна лишь при определённых условиях:
|
|
|
ü объём производства определён точно;
ü продажи равномерны;
ü поставка запасов идёт без задержек.
Даже в странах с развитой рыночной экономикой её рассматривают как теоретическую. В этой модели не предусмотрен страховой запас (резерв) на случай непредвиденного роста объёма продаж и сбоев в поставках.
Другая проблема этой модели – невозможность точно определить затраты на хранение.
|
|
|
