 |
Основные методы уточнения корней уравнения
|
|
|
|
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
(ДГТУ)
Кафедра «Программное обеспечение вычислительной техники
И автоматизированных систем»
УТВЕРЖДАЮ:
Заведующий кафедрой ПОВТиАС
________________ Карапетянц А.А.
" ____ " ________________ 20___ г
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к учебной практике на тему:
«Программирование методов решения нелинейных уравнений»
Практикант Куранов Артем Гагикович Группа ВПР12
Специальность 09.03.04 Программная инженерия
Руководитель работы / Землянухин В.Н. /
Ростов-на-Дону
2015 г.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
(ДГТУ)
Кафедра «Программное обеспечение вычислительной техники
И автоматизированных систем»
УТВЕРЖДАЮ:
Заведующий кафедрой ПОВТиАС
________________ Карапетянц А.А.
" ____ " ________________ 20___ г
ЗАДАНИЕ
На учебную практику
Студент Куранов Артем Гагикович Группа ВПР12
Тема Программирование методов решения нелинейных уравнений _
Срок представления отчета к защите "_____" 2015 г.
Исходные данные для учебной практики задание научного руководителя _
Руководитель практики / Землянухин В.Н. /
Задание принял к исполнению _______________ / Куранов А.Г. /
«____» ___________2015 год
Теоретическая часть
Отделение корней
В общем случае отделение корней уравнения f(x)=0 базируется на известной теореме, утверждающей, что если непрерывная функция f(x) на концах отрезка [a,b] имеет значения разных знаков, т.е. f(a)×f(b)< 0, то в указанном промежутке содержится хотя бы один корень. Например, для уравнения f(x)=x3-6x+2=0 видим, что при 
при 
что уже свидетельствует о наличии хотя бы одного корня.
|
|
|
Для уравнения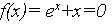 
видим, что 
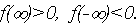Обнаружив, что 
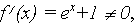устанавливаем факт наличия единственного корня, и остается лишь найти его (как говорится, за немногим стало дело).
Если предварительный анализ функции затруднителен, можно “пойти в лобовую атаку”. При уверенности в том, что все корни различны, выбираем некоторый диапазон возможного существования корней (никаких универсальных рецептов!) и производим “прогулку” по этому интервалу с некоторым шагом, вычисляя значения f(x) и фиксируя перемены знаков. При выборе шага приходится брать его по возможности большим для минимизации объема вычислений, но достаточно малым, чтобы не пропустить перемену знаков.
Рис. 3. Графическая интерпретация решения уравнения tg(x)=1/x
Часто на помощь приходит и графическая интерпретация задач (рис.3). Так, например, для упомянутого уравнения tg(x)=1/x можно построить графики двух элементарных функций y = tg(x) и y = 1/x и убедиться, что их пересечение происходит при значениях аргумента из диапазонов 
k=0, ± 1, ± 2,…. Теперь можно выбрать интересующий нас интервал и провести уточнение корня до заданной точности.
Прежде чем говорить об уточнении корней, несколько слов об обеспечении точности. Не надейтесь никогда найти точное значение корня и добиться обращения функции в нуль при использовании калькулятора, где сами числа представлены ограниченным числом знаков. Здесь критерием может служить абсолютная или относительная погрешность корня. Если корень близок к нулю, то лишь относительная погрешность даст необходимое число значащих цифр. Если же он весьма велик по абсолютной величине, то критерий абсолютной погрешности часто дает совершенно излишние верные цифры. Для функций, быстро изменяющихся в окрестности корня, может быть привлечен и критерий: абсолютная величина значения функции не превышает заданной допустимой погрешности.
|
|
|
Основные методы уточнения корней уравнения
|
|
|
