 |
Метод касательных (Ньютона)
|
|
|
|
Другую обширную группу методов уточнения корня представляют итерационные методы - методы последовательных приближений. Здесь в отличие от методов дихотомии и хорд задается не начальный интервал местонахождения корня, а его начальное приближение.
Наиболее популярным из итерационных методов является метод Ньютона (метод касательных).
Пусть известно некоторое приближенное значение Zn корня X*. Применяя формулу Тейлора и ограничиваясь в ней двумя членами, имеем
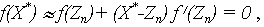
откуда
Геометрически этот метод предлагает построить касательную к кривой y=f(x) в выбранной точке x= Zn, найти точку пересечения её с осью абсцисс и принять эту точку за очередное приближение к корню (рис. 7).
Очевидно, что этот метод обеспечивает сходящийся процесс приближений лишь при выполнении некоторых условий (например, при непрерывности и знакопостоянстве первой и второй производной функции в окрестности корня) и при их нарушении либо дает расходящийся процесс (рис. 8), либо приводит к другому корню (рис. 9).
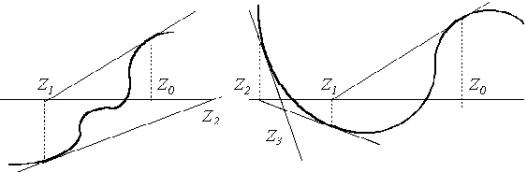
| Рис. 8 | Рис. 9 |
Очевидно, что для функций, производная от которых в окрестности корня близка к нулю, использовать метод Ньютона едва ли разумно.
Если производная функции мало изменяется в окрестности корня, то можно использовать видоизменение метода
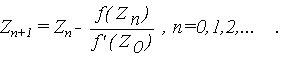
Существуют и другие модификации метода Ньютона.
Метод простой итерации
Другим представителем итерационных методов является метод простой итерации. Здесь уравнение f(x)=0 заменяется равносильным уравнением x= 
(x) и строится последовательность значений
Xn+1 = (Xn), n=0,1,2,....
Если функция (x) определена и дифференцируема на некотором интервале, причем | ’ (x) |< 1, то эта последовательность сходится к корню уравнения x= (x) на этом интервале.
|
|
|
Геометрическая интерпретация процесса представлена на рис. 10-12. Здесь первые два из них демонстрируют одностороннее и двустороннее приближение к корню, третий же выступает иллюстрацией расходящегося процесса (| ’ (x) | > 1).
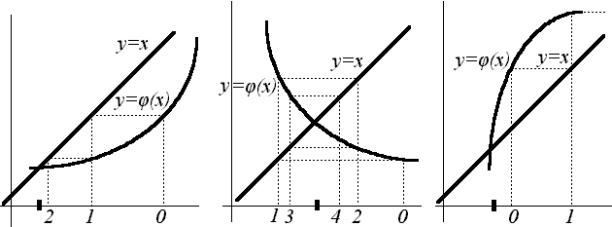
| Рис. 10 | Рис. 11 | Рис. 12 |
Если f’(x) > 0, то подбор равносильного уравнения можно свести к замене x=x- 
·f(x), т.е. к выбору (x)= x- ·f(x), где >0 подбирается так, чтобы в окрестности корня
0 < ’ (x)= 1- ·f’(x)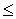 
1. Отсюда может быть построен итерационный процесс
’
где M 
max| f’(x)| (в случае f’(x)<0 возьмите функцию f(x) с противоположным знаком).
Возьмем для примера уравнение x3 + x -1000 = 0. Очевидно, что корень данного уравнения несколько меньше 10. Если переписать это уравнение в виде x =1000 - x3 и начать итерационный процесс при x0=10, то из первых же приближений очевидна его
расходимость. Если же учесть f’(x)=3x2+1>0 и принять за приближенное значение максимума f’(x) M=300, то можно построить сходящийся итерационный процесс на основе представления
.
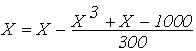Можно и искусственно подобрать подходящую форму уравнения, например:
или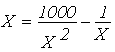 
.
.
Заметим, что существуют и другие методы (наискорейшего спуска, Эйткена-Стеффенсена, Вегстейна, Рыбакова и т.д.) уточнения корней, обладающие высокой скоростью сходимости.
Постановка задачи
Задание 1. Выполните отделение корней с использованием табулирования функции на отрезке и найдите один из корней методами дихотомии и хорд с относительной погрешностью до 0.001. Сравните объем вычислений при использовании указанных методов.
Функция: x^5 +12x^3-6x^2+x-10=0
Задание 2. Выполните отделение корней с использованием графической оценки и найдите один из корней методами Ньютона и простой итерации с относительной погрешностью до 0.001. Сравните объем вычислений при использовании указанных методов.
Функция: 7^x-6x =2
Отделение Корней
| Табулирование функции: x5 +12x3-6x2+x-10=0 | Построение графика функции: 7x-6x =2 | ||
| x | F(x) |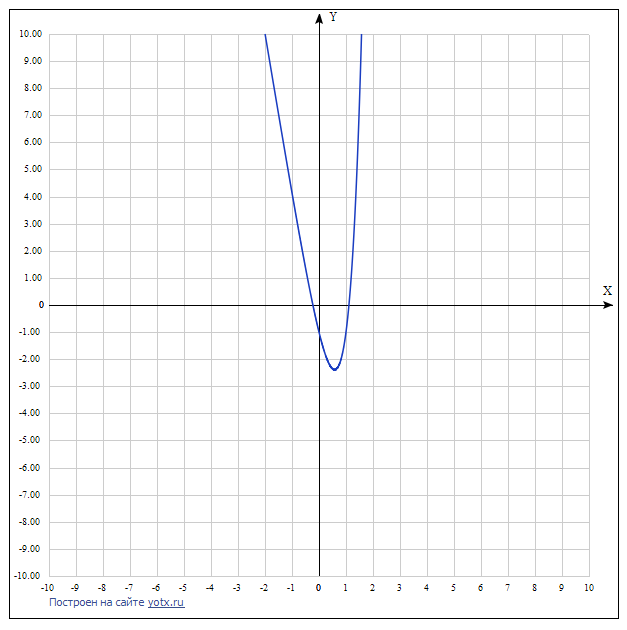 
| |
| -3 | -634 | ||
| -2.5 | -335.16 | ||
| -2 | -164 | ||
| -1.5 | -73.09 | ||
| -1 | -30 | ||
| -0.5 | -13.53 | ||
| -10 | |||
| 0.5 | -9.47 | ||
| -2 | |||
| 1.5 | 26.09 |
|
|
|
|
|
|
