Эксперименты по дифракции микрочастиц

Интегральные и спектральные характеристики теплового излучения

Тепловое излучение - испускание э/м волн нагретыми телами за счет их внутренней энергии (причиной излучения является возбуждение атомов, молекул вещества вследствие их теплового движения);

Тепловое излучение имеет место при любой температуре Т > 0 К; однако при невысоких температурах излучаются практически лишь длинные (инфракрасные λ_m2 ~ 1…10 мкм) э/м волны, а при высоких температурах излучателя доминирует ультрафиолетовая (λ_m1 ~ 0,1 мкм) область в спектре излучения.

Единственным видом э/м излучения, которое может находиться в термодинамическом равновесии с излучающими телами, является тепловое излучение.

Если поместить в замкнутую отвакуумированную полость с идеально отражающими стенками тела с различными температурами, то в такой системе начнется теплообмен путем испускания и поглощения э/м волн между телами и телами и стенками полости. Через некоторое время неизбежно установится термодинамическое равновесие в этой системе, соответствующее определенной температуре Трав. За любой промежуток времени испускаемая телами энергия становится равной поглощаемой энергии. Такое состояние излучения в полости остается неизменным во времени (в отсутствии внешних воздействий).

Способность теплового излучения находиться в равновесии с излучающими телами обусловлена тем, что его интенсивность возрастает при увеличении температуры.

Энергетическая светимость – интегральная характеристика теплового излучения.

Энергетической светимостью R_э называется величина, измеряемая потоком э/м излучения Ф_э, испускаемым единицей поверхности тела (с температурой Т) по всем направлениям (в пределах телесного угла 2 π, т.е. в полусферу): R_э = Ф_э / S, [Вт/м²], где S – площадь излучающей поверхности.

Распределение энергии в спектре излучения описывается спектральной плотностью энергетической светимости или испускательной способностью тела: r_{ω, T} = dR_{ω, T} / dω, [Дж/м^2.рад], где dR_{ω, T} - мощность излучения, испускаемая в узком спектральном интервале dω единицей поверхности при заданной Т.

Испускательная способность зависит от температуры Т и частоты ω (или длины волны λ), т.е. является функцией: r_ω,T = f (ω, T) (или функцией: r_{λ, T} = f’ (λ, T)).

Если известна функция r_ω,T, то энергетическая светимость может быть определена как: R_э = или R_э = , где dω и dλ – принадлежат одному и тому же спектральному интервалу и, соответственно, равны элементарные мощности:

dR_ω,T = dR_{λ, T} или r_ω,T ^. dω = r_λ,T ^. dλ формулы преобразования

 

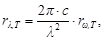Поглощательная способность тела – это отношение поглощённого единицей поверхности тела лучистого потока dΦ”_ω, заключённого в узком спектральном интервале [ω, ω+dω], к потоку излучения dΦ_ω, падающему на 1 поверхности в этом же спектральном интервале, т.е.

Тело, у которого поглощательная способность а_ω,T = 1, называется абсолютно чёрным. Реальные тела, для которых а_ω,T < 1, называются серыми.

Модель абсолютно чёрного тела (АЧТ)

Почти замкнутая полость с малым отверстием, через которое проникает внутрь излучение (тепловой луч). Температура стенок поддерживается постоянной. Попавшее излучение после многократных отражений от внутренних стенок практически полностью поглотится ими. Поэтому само малое отверстие можно принять за АЧТ, так как для него а _{ω, T} = 1 (отверстие полностью поглотило излучение).

Закон Кирхгофа

Формулировка. Отношение испускательной способности к поглощательной способности не зависит от природы тела (вещества) и является для всех тел одной и той же (универсальной) функцией частоты (или длины волны) и температуры.

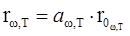Вывод. Зная испускательную способность АЧТ, и определив экспериментально спектральный коэффициент поглощения для рассматриваемого тела, можно определить испускательную способность этого тела (как серого тела):

 

Закон Стефана – Больцмана

Йозеф Стефан анализируя экспериментальные данные по излучению реальных (серых) тел, пришел к выводу, что энергетическая светимость R_э любого тела пропорциональна четвертой степени абсолютной температуры.

Людвиг Больцман получил выражение для энергетической светимости АЧТ:

где σ = 5,67. 10–8 Вт/(м2.К4)– постоянная Стефана – Больцмана. Для серых тел закон излучения должен быть дополнен поправочным коэффициентом ε = RЭсер / RЭ0 < 1, который часто называют степенью черноты. Поэтому закон принимает вид: R _{Э сер} = e ^. σ ^. Т ⁴

Закон смещения Вина

Вильгельм Вин показал, что универсальная функция Кирхгофа должна иметь вид:

f (ω, T) = ω^3. F (ω/ T) (формулой Вина)

где F (ω/ T) – некоторая функция отношения частоты излучения к температуре.

Формулировка. Длина волны в спектре излучения АЧТ, соответст-вующая наибольшей испускательной способности λ_m, обратно пропорциональна абсолютной температуре Т тела

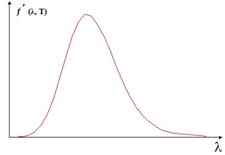
Площадь под кривой есть энергетическая светимость АЧТ: где b = 2,9 ^. 10^–3(м ^. К) – постоянная Вина

Формула Рэлея – Джинса

Джон Рэлей и Джеймс Джинс (предписывая каждому колебанию, связанному с электромагнитной волной излучения, среднюю энергию < E > = k ^. T) получили выражение для универсальной функции Кирхгофа (или испускательной способности АЧТ):

 

где k = 1,38.10–23 Дж/К – постоянная Больцмана

Интегрирование этой функции по λ в пределах [0; ∞] дает бесконечное значение. Этот результат, получил название «ультрафиолетовой катастрофы: р авновесие между излучением и излучающим телом устанавливается при конечных значениях плотности лучистой энергии.

Квантовая гипотеза и формула Планка

излучение испускается телами не непрерывно, а порциями (или квантами) энергии, величина которых пропорциональна частоте излучения:

или

где h = 6,62 ^. 10^–34 Дж ^. с, ħ = h /2π = 1,055 ^. 10^–34 Дж ^. с- постоянная Планка

h часто называют «квантом действия»

Если излучение испускается квантами (порциями), то полная энергия Eп излучения должна быть кратной этой величине, т.е. в общем случае:

где n = 0, 1, 2, 3,…

Выражение для средней энергии излучения с частотой ω:

 

Замечание. Если ħ →0, то формула переходит в классическое выражение

т.о, если бы энергия могла принимать непрерывный ряд значений, то ее среднее значение было бы равным kT.

Для спектрального интервала d ω на единицу объема полости, в которой заключено излучение, приходится dn _ω - элементарное число стоячих электромагнитных волн, равно:

 

Формулы Планка для АЧТ:

спектральную плотность (объемную) энергии равновесного теплового излучения:

Универсальная функция Кирхгофа f (ω, T) (или, иначе, испускательная способность АЧТ r _{0ω, T}) связана с функцией w (ω, T):

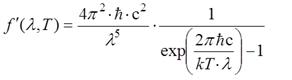
Формулы Планка точно совпадают с экспериментом во всем спектральном диапазоне [0; ∞] и могут быть использованы в расчетах.

 

Фотоэффектом (внешним) называется испускание (эмиссия) электронов веществом под действием света в окружающую среду (вакуум).

Обычно «вырываются» фотоэлектроны с поверхности твердых тел (проводников-металлов и полупроводников) Фотоэффект был открыт Г. Герцем

Внутренний фотоэффект - когда фотоэмиссии не наблюдается, а происходит только высвобождение электронов из атомов в пределах самого облучаемого вещества и наблюдается увеличение электропроводности вещества.

4) фотоэффект практически безынерционное явление – промежуток времени между началом освещения поверхности и появлением фототока не превышает -0,1 …1нс

По Эйнштейну: падающее монохроматическое излучение - поток фотонов с энергией Эйнштейн объяснил внешний фотоэффект как неупругое столкновение фотонов с электронами вещества. При поглощении фотона его энергия целиком передается одному электрону; при этом электрон приобретает кинетическую энергию не постепенно, а мгновенно. Часть энергии () затрачивается на освобождение электрона из металла, т.е. на преодоление потенциального барьера у поверхности тела (металла) - на совершение работы выхода (А), а оставшаяся часть – переходит в кинетическую энергию вылетевшего с облучаемой поверхности фотоэлектрона.

формула Эйнштейна: ħ𝜔 = А + Кmax, где Кmax =

C позиций А. Эйнштейна «красная граница» фотоэффекта получается в виде условия: или .

Эффект Комптона

Комптон исследовал рассеяние жесткого (характеристического) рентгеновского излучения на образцах (мишенях), материал которых состоял из легких атомов, например – графит или парафин. Источником излучения служила рентгеновская трубка с молибденовым антикатодом. Диафрагмы позволяли выделить узкий монохроматический пучок характеристического излучения и направить его на мишень. Спектральный состав рассеянного излучения исследовался с помощью рентгеновского спектрографа, состоящего из системы диафрагм Д, рабочего кристалла Кр и счетчика Сч с ионизационной камерой. Спектрограф допускал поворот в горизонтальной плоскости.

А. Комптон обнаружил, что в рассеянном излучении, наряду с исходной длиной волны λ, содержатся также лучи с большей длиной λ′ > λ; причем разность Δλ = λ′- λ оказалась зависящей только от угла рассеяния θ излучения и не зависила от материала мишени (в случае рассеивании на легких элементах!) и длины волны λ падающего излучения. Было установлено, что с увеличением угла θ интенсивность I смещенной компоненты (λ′) – растет, а исходной (λ) – падает.

Комптон истолковал это явление как упругое столкновение рентгеновского фотона (кванта) со свободным или слабо связанным электроном атома рассеивающего вещества, в результате чего фотон меняет направление распространения (рассеивается под углом θ) и отдает часть своей энергии электрону, который в этом процессе проявляется как «электрон отдачи».

- комптоновская длина волны (при рассеивании на электронах) получаем для разности длин волн фотона (до и после столкновения) - называют комптоновским смещением длины волны фотона. Для электрона: = 0,0243 А°= 2,43 пм.

 

Дуализм волновых и корпускулярных свойств излучения

Л. де Бройль предположил, что соотношения типа и 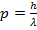, записанные для фотонов, работают и для вещественных микрочастиц, а движение любой частицы представляется волновым процессом, длина волны которого равна: λ Б = , а частота ω = . λ Б - дебройлевская длина волны частицы с импульсом р, равным (mv). Фазовая скорость дебройлевской волны через волновое число: 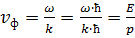(k = )

1. Для случая нерелятивистской свободной частицы имеем:

λБ = , (здесь учтено: и К=Е)

2. Для случая релятивистской частицы имеем:

λБ = (здесь учтено: )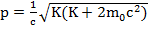

Простейшей волной с частотой ω и волновым вектором является плоская монохроматическая волна, описываемая функцией комплексного вида:

Ψ() = 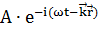, с учетом того, что для микрочастицы выполняется 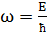и , то можно записать для плоской волны де Бройля, распространяющейся в направлении : Ψ( ) =

Эксперименты по дифракции микрочастиц

1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: