Волновая функция, ее статистическая интерпретация и физический смысл

В соответствии с корпускулярно-волновым дуализмом в квантовой механике состояние частицы задается (описывается) «пси» - функцией Ψ (r, t).

Согласно Максу Борну движение любой микрочастицы в отдельности подчиняется вероятностным законам. Распределение вероятности проявляется в регистрации достаточно большого числа частиц. Это распределение оказывается таким же, как распределение интенсивности волны, а именно: там, где интенсивность больше, регистрируется и бóльшее число частиц. Он записывает: dP = κ ^. A ^2. dV (1) т.е. квадрат амплитуды световой волны в данной точке является мерой вероятности попадания фотонов в эту точку (в объем dV).

Волновая функция Ψ (r, t) должна интерпретироваться – статистически, т.е. она является величиной, которая позволяет находить все вероятности.

Вероятность нахождения частицы в момент времени t с координатами [ x; x + dx ], [ y; y + dy ], [ z; z+ dz ] или, иначе, в объеме dV =dx ^. dy ^. dz можно определить через квадрат «пси»-функции: dP = |Ψ|^2. dV = Ψ ^. Ψ^*. dV, где Ψ^* - комплексно-сопряженная функция (с Ψ). За меру интенсивности волновой функции принимается квадрат ее модуля.

Физический смысл Ψ-функции проявляется через плотность вероятности, т.е. вероятность нахождения частицы в единице объема: dP / dV = |Ψ|² = Ψ ^. Ψ^*

Вероятность нахождения частицы в момент времени t в некотором конечном объеме можно определить, как интеграл: P = ∫ dP = ∫|Ψ|^2. dV

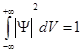Условие нормировки: Волновая функция должна удовлетворять условию нормировки: где Ψ = Ψ(x, y, z, t) – нормированная волновая функция,

 

и предполагается, что Ψ ≠ 0

Волновая функция должна быть:

• конечной (К), потому что вероятность не может быть больше 1;

• однозначной (О), так как вероятность не может быть неоднозначной величиной;

• непрерывной (Н), потому что вероятность не может изменяться скачком.

Дополнительные условия:

• гладкость Ψ-функции, т.е. отсутствие изломов;

• непрерывность производных типа и т.п.

 

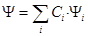Принцип суперпозиции: Если какая-либо квантовомеханическая система (частица или совокупность частиц) может находиться в состояниях, описываемых волновыми функциями Ψ₁, Ψ₂,… Ψ_i, то она может также находиться в состоянии Ψ, описываемом линейной комбинацией этих функций, т.е.

где C_i – некоторые постоянные коэффициенты в виде произвольных (в общем случае комплексных) чисел, квадрат модуля которых |С_i| ² определяет вероятность того, что система, представленная состоянием Ψ, может оказаться в состоянии Ψ_i. Иначе говоря, функция Ψ_i имеет некоторый «вес» С_i в линейной комбинации Ψ.

 

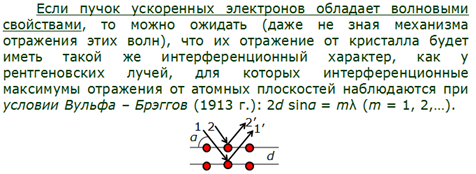
Эксперименты Дэвиссона и Джермера по дифракции микрочастиц

 

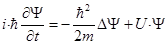Шрёдингер записал фундаментальное уравнение для нерелятивистской частицы во внешнем силовом поле относительно волновой функции. «Нерелятивистское временное (общее) уравнение Шрёдингера»:

(*) где m – масса частицы, U = U (x, y, z, t) – потенциальная функция частицы в силовом поле, i = 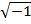– мнимая единица

оператор Лапласа в декартовой системе координат, ħ = h /2π – постоянная Планка.

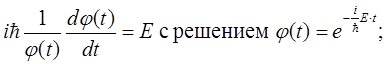Стационарные состояния – это состояния, в которых наблюдаемые физические величины не изменяются во времени. Если силовое поле, в котором движется частица, стационарно, т.е. потенциальная функция U = U (x, y, z) и не зависит от времени, то решение уравнения (*) можно представить в виде произведения двух функций: Ψ(x, y, z;t) = ψ(x, y, z) ^. φ(t)

временное

 

Координатное

с учетом, что ψ(x,y,z) ≠ 0

уравнением Шрёдингера для стационарных состояний:

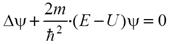
В случае стационарного силового поля состояние частицы будет описываться полной волновой функцией: Ψ(x, y, z;t) = ψ(x, y, z) ^.e ^{– i/ħ ( E t )}

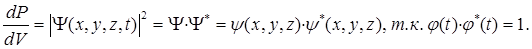В стационарном состоянии плотность вероятности выражается только через координатную часть волновой функции и не зависит от t:

 

 

В стационарное уравнение Шрёдингера в качестве параметра входит полная энергия Е частицы. Такие уравнения имеют бесчисленное множество решений, но из них путем наложения граничных условий отбирают решения, имеющие физический смысл. Условия: условия регулярности волновых функций: волновые функции вместе со своими первыми производными должны быть конечны, однозначны, непрерывны (условия КОН) а также гладкими (не иметь изломов) даже там, где потенциальная энергия U терпит разрыв.

Реальный физический смысл имеют только решения уравнения, выражаемые регулярными пси-функциями. Регулярные решения (ψ) возможны лишь при некотором определенном наборе значений энергии Е, характерном для данной задачи. Эти значения энергии Е₁, Е₂,…, Е_n называют собственными значениями энергии, а сами решения ψ₁, ψ₂,…, ψ_n при этом называют собственными функциями. В существовании собственных значений Е _n и собственных функций ψ_n заключается естественный и общий принцип квантования. Собственные значения Е _n принимаются за возможные значения энергии частицы в соответствующих стационарных состояниях. Эти значения (набор) Е _n могут образовывать: либо сплошной энергетический спектр в случае движения полностью свободной частицы в пространстве;

• либо дискретный энергетический спектр в случае ограниченного силовым внешним полем (U) движения частицы в пространстве.

Частица в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками -первое приближение силового поля, связывающего электроны в атоме, а также атомы в кристаллической решетке.

Рассматриваемая «яма» описывается следующей потенциальной функцией:

где l – ширина ямы.

Предполагается, что изначально микрочастица находится внутри ямы, стенки ямы являются идеально отражающими, и частица не может покинуть яму.

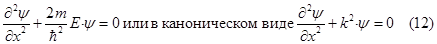В пределах ямы (0 ≤ х ≤ l) волновая функция частицы удовлетворяет стационарному уравнению Шрёдингера:

 

 

где k ²=2 mE/ħ ² (12*) С учетом характеристического уравнения λ²+ k ^2. λ =0 c мнимыми корнями λ_1,2= 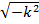имеем общее решение уравнения (12):

ψ(х) = А ^. sin kx + B ^. cos kx. Граничные условия на волновую функцию ψ(0)=ψ(l)=0 диктуют выбор коэффициента В =0, и, следовательно, получаем частное решение уравнения (12): Ψ(х) = A ^. sin kx

Так как пси-функция должна быть непрерывной внутри и вне ямы, то на границах (стенках) ямы должны выполняться условия:

причем последнее условие выполняется, когда kl = ± π n (n = 1, 2, 3,…). Определяя k =± πn / l и подставляя в выражение (12^*) для k ², получаем собственные значения полной энергии частицы: где n = 1, 2, 3,…

 

 

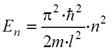
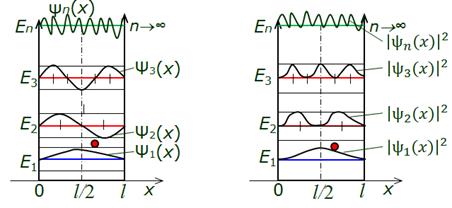
Из рисунка видно, что в состоянии с n = 2 частица не может находиться в центре ямы, но одинаково часто может пребывать в левой и правой половинах ямы. С увеличением энергии (n ­) максимумы функции 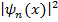располагаются все ближе друг к другу (функция сильно осциллирует), и при очень больших чисел n ® ∞ картина распределения 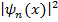практически сливается и становится равномерной, т.е. частица начинает вести себя совсем «по-классически». Выводы по задаче о потенциальной яме:

1. Даже в основном состоянии с n = 1 полная энергия частицы отлична от «0» и равна .
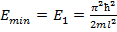2. Энергия микрочастицы – квантуется, т.е. принимает ряд дискретных значений En.
3. Дискретный характер энергии проявляется для сравнительно малых масс (m) и малых областей (l).
4. При n ® ∞ квантовое распределение энергии частицы переходит в классическое (непрерывное).

 

 

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: