Главная | Обратная связь | Поможем написать вашу работу!

Определение вероятностной продолжительности выполнения работ

Наряду с совмещением СМР важнейшей характеристикой календарного плана является продолжительность каждой работы и проекта в целом. При известных трудоемкостях каждой СМР процесс управления продолжительностью заключается в назначении на каждую из них определенного количества рабочих. Однако следует отметить, что на протяжении всего периода строительства численность рабочих на каждой СМР может варьироваться в некоторых пределах. Это связано с влиянием на строительный процесс ряда случайных факторов, которые трудно поддаются формализации: болезни рабочих, забастовки, перебои с поставками строительных материалов, отсутствие средств и заказчика и т.д. Следовательно, продолжительность любой СМР можно рассматривать как случайную величину, подчиняющуюся определенному закону.

В большинстве случаев не удается однозначно определить продолжительность выполнения каждой работы. Тогда используются оценки следующего вида:

· минимальная продолжительность выполнения работы (t_min);

· максимальная продолжительность (t_max);

· наиболее вероятная (плановая) продолжительность.

При оценке продолжительности работы у экспертов возникает трудность в определении наиболее вероятной продолжительности выполнения работ. Поэтому на практике часто ограничиваются двумя первыми оценками. Поскольку продолжительность работы – величина вероятностная, то необходимо выбрать закон распределения для ее моделирования. В случае двух оценок продолжительности работы принято использовать бета-распределение следующего вида:

. (21)

Оценка надежности календарного плана

Лист ГОУ – ВПО – ВГАСУ 10-8-20673

Под надежностью календарного плана понимается вероятность выполнения работ календарного плана в плановый срок. Иными словами, нужно спрогнозировать, какова будет действительная продолжительность выполнения работ.

Такой прогноз называется точечным. И вполне естественно, что истинное значение продолжительности выполнения работ будет отличаться от предсказанного. Поэтому на практике определяют не точечный прогноз, а доверительный интервал случайной величины, т.е. интервал, в который с заданной вероятностью попадает случайная величина. Вероятность попадания случайной величины в интервал определяется по формуле:

, (22)

где - задаваемая вероятность (в курсовом проекте принимается ); m_t – математическое ожидание, которое определяется по формуле

где t_i – статистические данные о продолжительности выполнения работ; N – объем статистических данных; -среднеквадратичное отклонение,которое определяется по формуле:

. (23)

Анализируя формулу (22), можно прийти к заключению, что для определения доверительного интервала необходимо знание закона распределения случайной величины и статистических данных, с помощью которых можно определить математическое ожидание m_t и среднеквадратичное отклонение . Законом распределения случайной величины (продолжительности выполнения работ) в курсовом проекте принимается бета-распределение. Для определения m_t и необходимы статистические данные. Если они отсутствуют, то можно воспользоваться алгоритмом статистического моделирования. Вводим следующую информацию:

· шифр работы (i=1,…,N);

· название работы;

· трудоемкость i -ой работы (Q_i);

· минимальное и максимальное число рабочих для выполнения i -ой работы (N_min; и N_maxi);

· количество работ, которые должны предшествовать данной;

Лист ГОУ – ВПО – ВГАСУ 10-8-2073

коэффициенты технологического совмещения смежных работ по началу и по концу рассчитываются по известным зависимостям из базы данных коэффициентов.

Продолжительность работ при реализации N=10 проектов T=561 день; T_min=0,8*t=449 день; T_max=1,3*t=729 день. Необходимо смоделировать продолжительности выполнения работ.

Используя формулу (21), определим

Используем алгоритм моделирования продолжительности работ.

Лист ГОУ – ВПО – ВГАСУ 10-8-2073

Лист ГОУ – ВПО – ВГАСУ 10-8-2073

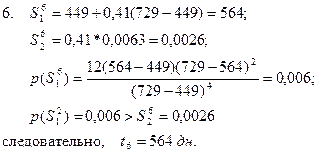
Математическое ожидание:

Среднеквадратичное отклонение:

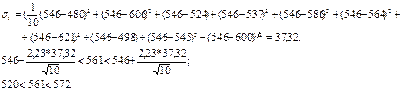
Таким образом, надежность календарного плана составляет 95%.

Лист ГОУ – ВПО – ВГАСУ 08-8-2457

Лист ГОУ – ВПО – ВГАСУ 10-8-2073

СЕТЕВОЙ ГРАФИК

Сетевые модели позволяют лучше всего отобразить порядок возведения сложного объекта, осуществлять научно – обоснованные методы строительства, определять и разрешать многие проблемные ситуации, возникающие в процессе производства строительных работ.

Сетевой график является документом, позволяющим оперативно руководить строительством и перераспределять ресурсы в зависимости от фактического состояния строительства.

Сетевые графики наиболее целесообразны для сооружения сложных промышленных и других комплексов, где участвуют многие организации, причем сетевые графики учитывают все работы, от которых зависит успешный ход строительства, в т.ч. проектирование, внешние поставки материалов, технологического оборудования и др.

Условные обозначения сетевого графика

Работа

Событие

Фиктивная работа

Расчет сетевого графика начинается с определения ранних сроков. Ранние начала и окончания вычисляются последовательно от исходной до завершающей работы. Раннее начало исходной работы равно 0, раннее окончание – сумме раннего начала и продолжительности работы:

Раннее начало последующей работы равно раннему окончанию предыдущей работы. Если данной работе непосредственно предшествуют несколько работ, то её раннее начало будет равно максимальному из ранних окончаний предшествующих работ.

Расчет поздних сроков ведется в обратном порядке от завершающей до исходной работы. Позднее окончание завершающей работы равно ее раннему окончанию, т.е. продолжительности критического пути.

Лист ГОУ – ВПО – ВГАСУ 10-8-2073

Позднее окончание определяется как разность позднего окончания и продолжительности:

Полный резерв времени равен разности поздних и ранних сроков

Свободный резерв времени равен разности между минимальным ранним началом последующих работ и ранним окончанием данной работы.

Лист ГОУ – ВПО – ВГАСУ 10-8-2073

СПИСОК ЛИТЕРАТУРЫ

1. Баркалов С. А., Курочка П. Н., Мищенко В. Я. Моделирование и автоматизация организационно-технологического проектирования строительного производства – Воронеж, 1997 – 120 с.

2. Баркалов С. А., Косачев С. Ю. Имитационное моделирование календарного плана строительства объектов // Изд. ВУЗов. Строительство – 1998 - %11 – 12, с.68 – 72.

3. Бурков В. М., Новиков Д. А. Как управлять проектом – М.: Синтег – Гео, с.1997 – 188.

4. Бусленко В. Н. Автоматизация имитационного моделирования сложных систем – М.: Наука, 1997 – 240с.

5. Гусаков А. А. Выбор проектных решений в строительстве – М.: Стройиздат, 1982 – 372с.

6. Дикман Л. Г. Организация строительного производства – М.: Издательство АВС, 2002 – 512с.

7. СНиП 3.01.01-85. Организация строительного производства / Госстрой СССР. – М.: ЦИТП Госстроя СССР, 1985 – 56с.

Лист ГОУ – ВПО – ВГАСУ 10-8-2073

⇐ Предыдущая 1 2 3 45

Воспользуйтесь поиском по сайту: