Поголовье коров и удой молока

Практическое занятие 2

РАСЧЕТ СРЕДНИХ ВЕЛИЧИН

 

1. Средняя арифметическая. 1

2. Средняя гармоническая. 6

3. Средняя геометрическая. 8

4. Средняя квадратическая. 11

5. Мода и медиана. 18

Средняя арифметическая

 

Средняя арифметическая является наиболее распростра­ненной среди средних величин. Ее применяют в тех случаях, когда даны отдельные объекты с индивидуальными значения­ми признаков, выраженными абсолютными показателями. Среднюю арифметическую определяют как отношение сум­мы индивидуальных значений признаков к их количеству.

Различают среднюю арифметическую простую и взвешен­ную. Среднюю арифметическую простую применяют в слу­чае, если индивидуальные значения признака в совокупности встречаются по одному разу, а взвешенную - если индиви­дуальные значения признака представлены несколькими объ­ектами.

Среднюю арифметическую простую определяют по фор­муле:

,

где 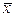-средняя;

х -варианты;

n -число вариант.

Формула средней арифметической взвешенной имеет вид:

,

где f -частота вариант.

Рассмотрим методику расчета средней арифметической.

Пример 1. Имеются данные по 8 коровам об их удое за год (табл. 2.1).

 

Т а б л и ц а 2.1

Удой коровы

№ коровы	Удой коровы за год, кг
х
Итого

Требуется определить средний удой на одну корову за год.

Так как даны индивидуальные значения удоя молока по каждой корове, то средний удой определяется по формуле средней арифметической простой:

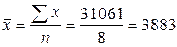кг.

Таким образом, среднегодовой удой от коровы за год составляет 3883 кг.

Технология решения задачи втабличном процессоре Microsoft Excel следующая.

1. Введите исходные данные в соответствии с рис. 2.1.

 

 

Р и с. 2.1

 

2. Рассчитайте средний удой на корову за год как среднюю арифметическую простую.

2.1. Выделите ячейку С11.

2.2. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Вставка функции> или выполните команду Вставка, f_x Функция, щелкнув поочередно левой кнопкой мыши.

2.3. В диалоговом окне Мастер функций - шаг 1 из 2 с помощью левой кнопки мыши установите: Категория ® <Статистические>, Выберете функцию ® <СРЗНАЧ> (рис. 2.2).

 

 

Р и с. 2.2

 

2.4. Щелкните левой кнопкой мыши на кнопке <ОК>.

2.5. На вкладке СРЗНАЧ установите параметры в соответствии с рис. 2.3.

 

 

Р и с. 2.3

 

2.6. Щелкните левой кнопкой мыши на кнопке <ОК>.

Результаты решения выводятся на экран дисплея в следующем виде (рис. 2.4).

 

 

Р и с. 2.4

 

Пример 2. Имеются данные по сельскохозяйственному предприятию о поголовье коров на фермах и среднегодовом удое коровы по каждой ферме (табл. 2.2).

 

Т а б л и ц а 2.2

Поголовье коров и удой молока

Ферма	Поголовье коров, гол.	Среднегодовой удой коровы, кг	Валовой надой молока, кг
f	х	xf
Итого		´

 

Требуется определить среднегодовой удой коро­вы за год по хозяйству.

Поскольку индивидуальные значения признака в совокуп­ности встречаются несколько раз (например, на ферме 1 − 230 раз), средняя определяется по формуле средней арифметической взвешенной. Для этого общий валовой надой молока по сельскохозяйственному пред­приятию необходимо разделить на все поголовье коров:

кг.

Среднегодовой удой молока коровы в целом по сельскохозяйственному предприятию составляет 4058 кг.

Технология решения задачи втабличном процессоре Microsoft Excel следующая.

1. Введите исходные данные в соответствии с рис. 2.5.

 

Р и с. 2.5

 

2. Рассчитайте общее поголовье.

2.1. Выделите ячейку D8.

2.2. Щелкните левой кнопкой мыши на панели инструментов на букве S кнопки <Автосумма > .

2.3. Выделите ячейки В2:В6.

2.4. Нажмите клавишу <Enter>.

3. Рассчитайте валовой надой молока за год.

3.1. Выделите ячейку D9.

3.2. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Вставка функции> или выполните команду Вставка, f_x Функция, щелкнув поочередно левой кнопкой мыши.

3.3. В диалоговом окне Мастер функций - шаг 1 из 2 с помощью левой кнопки мыши установите: Категория ® <Математические>, Выберете функцию ® <СУММПРОИЗВ> (рис. 2.6).

Р и с. 2.6

3.4. Щелкните левой кнопкой мыши на кнопке <ОК>.

3.5. На вкладке СУММПРОИЗВ установите параметры в соответствии с рис. 2.7.

 

 

Р и с. 2.7

 

3.6. Щелкните левой кнопкой мыши на кнопке <ОК>.

4. Рассчитайте среднегодовой удой молока от коровы по сельскохозяйственному предприятию как среднюю арифметическую взвешенную.Для этого введите в ячейку D10 формулу =D9/D8.

Результаты решения выводятся на экран дисплея в следующем виде (рис. 2.8).

 

 

Р и с. 2.8

Средняя гармоническая

 

Средняя гармоническая является обратной величиной средней арифметической, рассчитанной из обратных значе­ний признака. В качестве частот в этом случае используют­ся не единицы совокупности, а произведения этих единиц на значения признака.

Среднюю гармоническую применяют в тех случаях, когда известны индивидуальные значения и объемы признака, а частоты неизвестны.

Формула средней гармонической имеет вид:

,

где 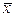-средняя;

х -варианты;

w - объемы явления.

Рассмотрим методику расчета средней гармонической.

Пример. Имеются данные по сельскохозяйственным предприятиям об общих затратах на производство молока и себестоимости 1 ц (табл. 2.3).

 

Т а б л и ц а 2.3

123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: