 |
Затраты на производство молока
|
|
|
|
| Предприятие | Затраты на производство молока, руб. | Себестоимость 1 ц молока, руб. | Производство молока, ц |
| w | x |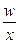 
| |
| Итого |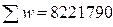 
| ´ | 
|
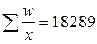
Требуется определить среднюю себестоимость 1 ц молока по всем предприятиям.
Для расчета средней необходимо определить общее производство молока по всем предприятиям и затраты на его производство. Средняя себестоимость 1 ц молока будет рассчитываться по формуле средней гармонической:
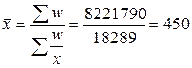руб.
Средняя себестоимость 1 ц молока по всем сельскохозяйственным предприятиям составляет 450 руб.
Технология решения задачи втабличном процессоре Microsoft Excel следующая.
1. Введите исходные данные в соответствии с рис. 2.9.
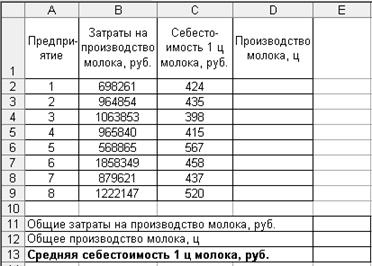
Р и с. 2.9
2. Рассчитайте производство молока по предприятиям.
2.1.Введите в ячейку D2 формулу =В2/С2.
2.2. Скопируйте ячейку D2 в ячейки D3:D9.
3. Рассчитайте общие затраты на производство молока.
3.1. Выделите ячейку Е11.
3.2. Щелкните левой кнопкой мыши на панели инструментов на букве S кнопки <Автосумма > 
.
3.3. Выделите ячейки В2:В9.
3.4. Нажмите клавишу <Enter>.
4. Рассчитайте общее производство молока. Для этого вставьте в ячейку Е12 математическую функцию =СУММ(D2:D9). Порядок расчетов изложен в пункте 3.
5. Рассчитайте среднюю себестоимость 1 ц молока как среднюю гармоническую. Для этого введите в ячейку Е13 формулу =E11/E12.
Результаты решения выводятся на экран дисплея в следующем виде (рис. 2.10).
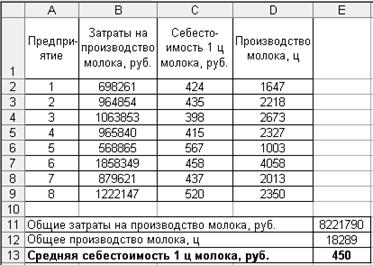
Р и с. 2.10
Средняя геометрическая
Средняя геометрическая — это средняя, в которой общий объем явления представляет произведение индивидуальных значений признака. Такую среднюю применяют в основном для расчета среднего темпа изменения какого-либо показателя за определенный промежуток времени.
|
|
|
Формула расчета средней геометрической имеет вид:
,
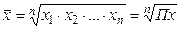где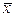 
-средняя;
х -варианты;
n -число вариант;
П — произведение.
Рассмотрим методику расчета средней геометрической.
Пример. Имеются данные об ежегодных темпах изменения поголовья крупного рогатого скота на сельскохозяйственном предприятии (табл. 2.4).
Т а б л и ц а 2.4
Коэффициенты роста поголовья крупного рогатого скота
| Год | Коэффициент роста поголовья |
| 0,942 1,021 0,995 1,084 1,152 |
Требуется определить средний коэффициент изменения поголовья крупного рогатого скота.
Так как общий объем прироста поголовья определяется как произведение коэффициентов роста, для определения среднего коэффициента роста необходимо применить среднюю геометрическую:
Средний рост поголовья крупного рогатого скота за 5 лет составил 1,036, то есть в среднем ежегодно поголовье увеличивалось в 1,036 раза или на 3,6%.
Технология решения задачи втабличном процессоре Microsoft Excel следующая.
1. Введите исходные данные в соответствии с рис. 2.11.
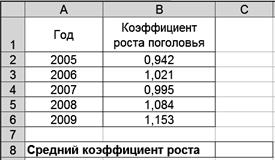
Р и с. 2.11
2. Рассчитайте средний коэффициент роста поголовья крупного рогатого скота как среднюю геометрическую.
2.1. Выделите ячейку С8.
2.2. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Вставка функции> 
или выполните команду Вставка, fx Функция, щелкнув поочередно левой кнопкой мыши.
2.3. В диалоговом окне Мастер функций - шаг 1 из 2 с помощью левой кнопки мыши установите: Категория ® <Статистические>, Выберете функцию ® <СРГЕОМ> (рис. 2.12).
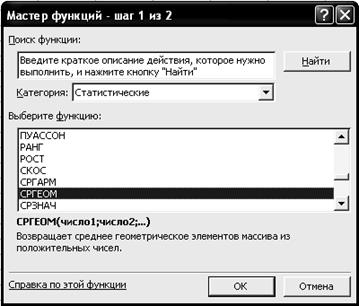
Р и с. 2.12
2.4. Щелкните левой кнопкой мыши на кнопке <ОК>.
2.5. На вкладке СРГЕОМ установите параметры в соответствии с рис. 2.13.
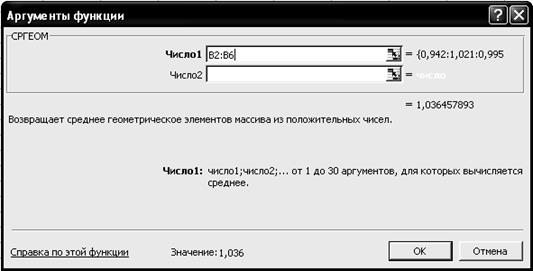
Р и с. 2.13
2.6. Щелкните левой кнопкой мыши на кнопке <ОК>.
|
|
|
Результаты решения выводятся на экран дисплея в следующем виде (рис. 2.14).
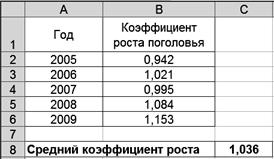
Р и с. 2.14
Средняя квадратическая
Среднюю квадратическую используют для признаков, выраженных линейными мерами площади. Например, для определения среднего диаметра корзинок подсолнечника, величины листьев, размера колоний микроорганизмов и др. Также как и средняя арифметическая, средняя квадратическая бывает простая и взвешенная.
Среднюю квадратическую простую определяют по формуле:
,
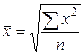где 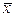-средняя;
х -варианты;
n -число вариант.
Формула средней квадратической взвешенной имеет вид:
,
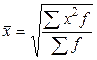где f -частота вариант.
Рассмотрим методику расчета средней квадратической.
Пример 1. Имеются данные о длине 10 шкурок кролика (табл. 2.5).
Т а б л и ц а 2.5
Длина шкурок кролика
| Шкурки | Длина шкурок, дм | Квадрат длины шкурок |
| х | х 2 | |
| 4,85 4,96 4,58 4,67 4,68 4,81 4,79 4,63 4,90 4,53 | 23,5225 24,6016 20,9764 21,8089 21,9024 23,1361 22,9441 21,4369 24,010 20,5209 | |
| Итого | ´ | 
|
Требуется определить среднюю длину шкурок.
Поскольку длина шкурок является линейной мерой их площади и признаки встречаются по одному разу, средняя длина определяется по формуле средней квадратической простой:
дм.
Средняя длина шкурок кролика составляет 4,74 дм.
Технология решения задачи втабличном процессоре Microsoft Excel следующая.
1. Введите исходные данные в соответствии с рис. 2.15.
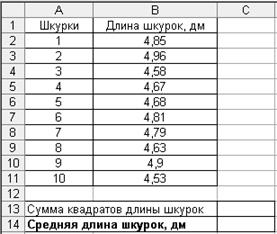
Р и с. 2.15
2. Рассчитайте сумму квадратов длины шкурок.
2.1. Выделите ячейку С13.
2.2. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Вставка функции> или выполните команду Вставка, fx Функция, щелкнув поочередно левой кнопкой мыши.
2.3. В диалоговом окне Мастер функций - шаг 1 из 2 с помощью левой кнопки мыши установите: Категория ® <Математические>, Выберете функцию ® <СУММКВ> (рис. 2.16).
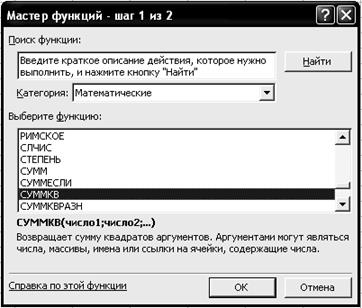
Р и с. 2.16
2.4. Щелкните левой кнопкой мыши на кнопке <ОК>.
2.5. На вкладке СУММКВ установите параметры в соответствии с рис. 2.17.
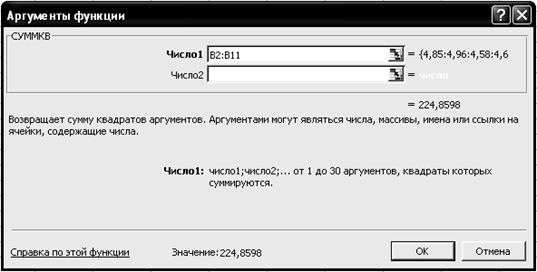
Р и с. 2.17
2.6. Щелкните левой кнопкой мыши на кнопке <ОК>.
3. Рассчитайте среднюю длину шкурок как среднюю квадратическую простую.
3.1. Выделите ячейку С14.
3.2. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Вставка функции> или выполните команду Вставка, fx Функция, щелкнув поочередно левой кнопкой мыши.
|
|
|
3.3. В диалоговом окне Мастер функций - шаг 1 из 2 с помощью левой кнопки мыши установите: Категория ® <Математические>, Выберете функцию ® <КОРЕНЬ> (рис. 2.18).
Р и с. 2.18
3.4. Щелкните левой кнопкой мыши на кнопке <ОК>.
3.5. На вкладке КОРЕНЬ установите параметры в соответствии с рис. 2.19.
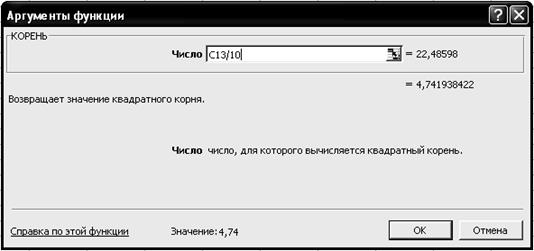
Р и с. 2.19
3.6. Щелкните левой кнопкой мыши на кнопке <ОК>.
Результаты решения выводятся на экран дисплея в следующем виде (рис. 2.20).
Р и с. 2.20
Пример 2. Имеются данные о диаметре сосков вымени у коровы (табл. 2.6).
Т а б л и ц а 2.6
|
|
|
