 |
Расчет ожидаемого срока службы
|
|
|
|
нелинейных ограничителей перенапряжений 110 ÷ 750 кВ
3. 1. Исходные положения
Расчет ожидаемого срока службы ОПН состоит в проверке надежности его работы при ограничении коммутационных перенапряжений в условиях конкретной электропередачи. Надежность ОПН является достаточной, если ожидаемый с доверительной вероятностью Рдов срок службы ОПН Nсл (ожидаемое число лет безаварийной работы) будет не менее нормируемого [4]. Нормированные значения срока службы ОПН приведены в табл. 3.1.
Таблица 3.1. Нормируемый срок службы ОПН при доверительной вероятности Рдов=0,98
| Uном, кВ | |||||
| Nсл, лет |
Методика расчета состоит из следующих этапов:
· расчет статистического распределения амплитуд неограниченных перенапряжений в точке установки ОПН;
· расчет статистического распределения ресурса, расходуемого резистором ограничителя в течение года;
· определение ожидаемого срока службы ОПН.
Оценка надежности ограничителей, установленных на питающем и на разомкнутом концах электропередачи (см. рис. 2.1), должна производиться раздельно, так как токовые нагрузки на них существенно отличаются.
В симметричном режиме амплитуда неограниченных перенапряжений К в относительных единицах (о.е.) определяется по формуле
К = КудU,
где Куд _ ударный коэффициент; U _ амплитуда вынужденной составляющей перенапряжений.
Ударный коэффициент характеризует вид коммутации и интенсивность переходного процесса, а вынужденная составляющая – схему и режим электропередачи.
Для каждого вида коммутации как в симметричном, так и в несимметричном режимах математическое ожидание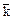 
, среднеквадратичное отклонение σк амплитуды неограниченных перенапряжений определяются по формулам:
|
|
|
; 
,
где 
и σу _ математическое ожидание и среднеквадратичное отклонение ударного коэффициента для соответствующей коммутации; 
и σu _ то же самое для вынужденной составляющей перенапряжений.
Если наименьшая из частот собственных колебаний коммутируемой электропередачи ωc ≥ 1,6ω, что характерно для большинства электропередач, то ударный коэффициент перенапряжений, возникающих на разомкнутом конце, Кудр статистически инвариантен относительно структуры и параметров этой передачи. В этом случае закон статистических распределений Кудр определяется только видом коммутации, а параметры этого закона 
и σур одинаковы для любой электропередачи независимо от ее сложности и класса номинального напряжения.
Ударный коэффициент перенапряжений, возникающих на питающем конце электропередачи, Кудп подчиняется тому же закону, что и ударный коэффициент перенапряжений на разомкнутом конце, однако значения его другие, т. е. Кудп ≠ Кудр и σуп ≠ σур.
На рис. 3.1 представлены зависимости 
и σуп/σур от безразмерного параметра d, значение которого зависит от параметров электропередачи и определяется по формуле
,
где Хп = Х1 _ для схемы электропередачи без шунтирующих реакторов
(см. рис. 2.1,а),
– для схемы с реакторами
(см. рис. 2.1,б);
(Х1 _ сопротивление предвключенной индуктивности на промышленной частоте; Z _ волновое сопротивление линии);
λ – волновая длина линии.
 |
Рис. 3.1. Зависимости отношений:
1 – 
; 2 – σуп/σур=f(d)
Для расчетов в системе относительных единиц применяются в качестве базисных значения параметров электропередачи, приведенные в
табл. 3.2.
Таблица 3.2. Базисные значения параметров электропередачи
| Uном, кВ | |||||
| Uбаз, кВ | |||||
| Zбаз, Ом | |||||
| Lбаз, Гн | 1,82 | 1,69 | 1,43 | 1,16 | 1,05 |
| Сбаз, мкФ | 5,6 | 6,0 | 7,1 | 8,7 | 9,7 |
| Iбаз, А | |||||
| Абаз∙10–3 | |||||
| А/Абаз | 1,71 | 1,75 | 1,76 | 1,77 | 1,75 |
|
|
|
Вольтамперная характеристика ОПН при коммутационных перенапряжениях
U = А∙Iα = A∙I0,04.
Статистические распределения неограниченных
|
|
|
