 |
Расходуемого ОПН в течение года
|
|
|
|
Ресурс, расходуемый ОПН в течение года
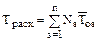 ,
,
где Ns _ ожидаемое число воздействий на ОПН в коммутации S_типа в течение одного года эксплуатации (табл. 3.3); 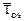 _ математическое ожидание ресурса, расходуемого в одной коммутации S_типа; n – количество видов коммутаций.
_ математическое ожидание ресурса, расходуемого в одной коммутации S_типа; n – количество видов коммутаций.
Математическое ожидание ресурса  определяется с помощью графического построения, показанного на рис. 3.6.
определяется с помощью графического построения, показанного на рис. 3.6.
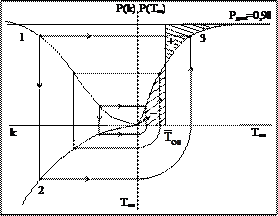 |
Рис. 3.6. Графическое определение математического ожидания ресурса
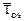 ,
,
отвечающего заданной доверительной вероятности Рдов :
1 – Р(k); 2 – k = f(Tos); 3 – P(Tos)
В третьем квадранте строится функция k = f(Tos), вычисляемая по формуле
 ,
,
где k – неограниченные перенапряжения в коммутации S_типа; A – коэффициент, значения которого приведены в табл. 3.2; bs – вспомогательный параметр.
Для электропередач 110÷330 кВ bs=1. Для электропередач 500, 750 кВ, если в точке установки ОПН включен шунтирующий реактор, коэффициент bs зависит от амплитуды неограниченных перенапряжений и равен bs = 1 + as/Xp. Усредненные значения коэффициента as приведены в табл. 3.5.
Таблица 3.5. Усредненные значения коэффициента as
| Uном, кВ | Значения k | |||||
| 1,9 | 2,1 | 2,3 | 2,5 | 2,7 | 2,9 | |
| 0,25 | 0,29 | 0,32 | 0,34 | 0,36 | 0,38 | |
| 0,27 | 0,31 | 0,34 | 0,38 | 0,38 | 0,4 |
Во втором квадранте (рис. 3.6) размещается функция статистического распределения амплитуд неограниченных перенапряжений, рассчитанная по методике разд. 3.2. Затем графическим путем, ход которого показан стрелками на рис. 3.6, строится функция статистического распределения ресурса, расходуемого ОПН в одной коммутации S_типа – P(Tos).
Математическое ожидание 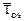 , отвечающее заданной доверительной вероятности, определяется графически следующим образом. Из точки на оси Р(Тоs), соответствующей значению Рдов, проводится прямая, параллельная оси Тоs (рис. 3.6). Затем проводится вертикальная линия, пересекающая функцию P(Tos), таким образом, чтобы заштрихованные площади, обозначенные на рис. 3.6 знаками «+» и «–», были равны. Точка пересечения этой прямой с осью Тоs дает искомое значение
, отвечающее заданной доверительной вероятности, определяется графически следующим образом. Из точки на оси Р(Тоs), соответствующей значению Рдов, проводится прямая, параллельная оси Тоs (рис. 3.6). Затем проводится вертикальная линия, пересекающая функцию P(Tos), таким образом, чтобы заштрихованные площади, обозначенные на рис. 3.6 знаками «+» и «–», были равны. Точка пересечения этой прямой с осью Тоs дает искомое значение 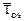 .
.
|
|
|
Количество расчетов P(Tos) должно соответствовать количеству расчетных коммутаций для заданной электропередачи.
Определение ожидаемого срока службы ОПН
Математическое ожидание срока службы ОПН определяется по формуле
 ,
,
где Тисх– исходный ресурс, которым обладает вновь изготовленный ОПН;  – математическое ожидание ресурса, расходуемого ОПН в процессе n коммутаций; Ns – ожидаемое число воздействий на ОПН (табл. 3.3);
– математическое ожидание ресурса, расходуемого ОПН в процессе n коммутаций; Ns – ожидаемое число воздействий на ОПН (табл. 3.3);  – математическое ожидание расходуемого ресурса при коммутации S _типа для заданного значения Рдов.
– математическое ожидание расходуемого ресурса при коммутации S _типа для заданного значения Рдов.
Значения исходного ресурса задаются техническими условиями на ОПН. Для ограничителей, изготавливаемых НПО «Электрокерамика»,
значения исходного ресурса [6] приведены в табл. 3.6.
Таблица 3.6. Исходный ресурс ОПН
| Uном, кВ | |||||
| Тисх, отн. ед. |
Пример расчета ожидаемого срока службы ОПН
Исходные данные
Требуется рассчитать ожидаемый срок службы ОПН, установленного в конце электропередачи 220 кВ, расчетная схема которой представлена на рис. 3.7.
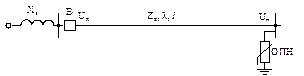 |
Параметры электропередачи: номинальное напряжение Uном= 220 кВ; длина линии l =80 км; волновое сопротивление линии по прямой последовательности Zл=405 Ом; волновое сопротивление линии по нулевой последовательности
 Ом; коэффициенты изменения фазы по прямой последовательности β=1,0704∙10–3 рад/км, по нулевой последовательности β(0)=1,6336∙10–3 рад/км. Реактивность питающей системы изменяется в течение года по прямой последовательности Х1макс=22 Ом, Х1мин=17, по нулевой последовательности
Ом; коэффициенты изменения фазы по прямой последовательности β=1,0704∙10–3 рад/км, по нулевой последовательности β(0)=1,6336∙10–3 рад/км. Реактивность питающей системы изменяется в течение года по прямой последовательности Х1макс=22 Ом, Х1мин=17, по нулевой последовательности  Ом,
Ом,  Ом. Длительность бестоковой паузы для успешного и неуспешного ТАПВ tапв=0,2 с.
Ом. Длительность бестоковой паузы для успешного и неуспешного ТАПВ tапв=0,2 с.|
|
|
Рис. 3.7. Расчетная схема электропередачи
Для заданной схемы электропередачи расчетными являются следующие виды коммутации с соответствующими максимальными значениями ЭДС питающей системы (табл. 2.1):
S1 – плановое включение ненагруженной линии, Емакс=1;
S2 – успешное ТАПВ, Емакс=1,15;
S4 – трехфазный разрыв электропередачи вследствие ликвидации несимметричного КЗ, Емакс=1,2;
S5 – неуспешное ТАПВ, Емакс=1,15.
Минимальное значение ЭДС системы для всех видов коммутации Емин=1.
3.5.2. Расчет вынужденных напряжений переходных процессов
В симметричном режиме
Расчет ведется по методике, изложенной в разд. 2.1.
• Плановое включение ненагруженной линии, S1.
Волновая длина линии по прямой последовательности l = b l =0,086 рад.
Волновая длина эквивалентной линии, замещающей Х1,
для Х1макс  рад;
рад;
для Х1мин  рад.
рад.
Вынужденное напряжение на разомкнутом конце линии
 ;
;
 .
.
Вынужденное напряжение на питающем конце линии
Uпмакс1 = Upмакс1cosλ = 1,0084соs0,086 = 1,005;
Uпмин1 = Upмин1cosλ = 1,0073соs0,086 = 1,0036.
Поскольку Uпмакс1 < 1,15, то учитывать насыщение магнитопроводов не нужно.
Математическое ожидание вынужденного напряжения на разомкнутом конце линии
 .
.
• Успешное ТАПВ, S2.
Поскольку значение Емин принято одинаковым для всех коммутаций, то Uрмин2=Uрмин1=1,0073 и Uпмин2=Uпмин1=1,0036.
Для данной коммутации Емакс=1,15, поэтому
Uпмакс2 = ЕмаксUпмакс1 = 1,15∙1,005 = 1,155, что больше 1,15.
Следовательно, необходим учет насыщения магнитопроводов.
Характеристики питающих трансформаторов неизвестны, поэтому примем Zбаз=10000 Ом, тогда
 рад;
рад;
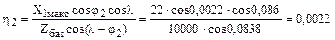 .
.
По кривым Uнас = f(η2,Uп) (см. рис. 2.2) для Uпмакс2=1,155 находим значение напряжения с учетом насыщения Uпнмакс2=1,15, тогда
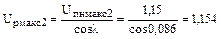 .
.
Математическое ожидание вынужденного напряжения на разомкнутом конце линии
 .
.
3.5.3. Расчет вынужденных напряжений переходных процессов
В несимметричном режиме
Определим коэффициенты несимметрии h при КЗ в начале линии и в конце линии при максимальных и минимальных реактивностях питающей системы. Расчет выполняется по методике, изложенной в разд. 2.2.
Примем равными реактивности системы при прямой и обратной последовательностях, тогда ν1=ν2=1 и  . Волновая длина линии по нулевой последовательности l(0) = b(0) l =0,131 рад.
. Волновая длина линии по нулевой последовательности l(0) = b(0) l =0,131 рад.
|
|
|
КЗ в конце линии при Х1макс=22 Ом и  Ом:
Ом:
 ;
;
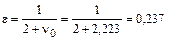 ;
;
 КЗ в начале линии при Х1макс=22 Ом и
КЗ в начале линии при Х1макс=22 Ом и  Ом:
Ом:
 ;
;  ;
;
 КЗ в конце линии при Х1мин=17 Ом и
КЗ в конце линии при Х1мин=17 Ом и  Ом:
Ом:
 ;
;
 ;
;
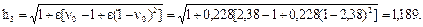 КЗ в начале линии при Х1мин=17 Ом и
КЗ в начале линии при Х1мин=17 Ом и  Ом:
Ом:
 ;
; 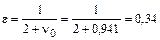 ;
;
 .
.
Для расчета минимальных значений вынужденных напряжений при несимметричных режимах примем hмин=0,99, а для максимальных значений – hмакс=1,172.
• Трехфазный разрыв электропередачи вследствие ликвидации несимметричного КЗ, S4.
Uпмин4=Uпмин1hмин=1,0036∙0,99=0,994;
Uрмин4=Uрмин1hмин=1,0073∙0,99=0,997.
Для данной коммутации Емакс=1,2, поэтому
Uпмакс4=ЕмаксUпмакс1hмакс=1,2∙1,005∙1,172=1,413, что больше1,15.
Следовательно, необходим учет насыщения магнитопроводов.
По кривым Uнас=f(η2,Uп) (рис. 2.2) для Uпмакс4=1,413 и η2=0,0022 находим значение напряжения с учетом насыщения Uпнмакс4=1,39, тогда
 .
.
Математическое ожидание вынужденного напряжения на разомкнутом конце линии
 .
.
• Неуспешное ТАПВ, S5.
Uпмин5=Uпмин4=0,994; Uрмин5=Uрмин4=0,997.
Для данной коммутации Емакс=1,15, поэтому
Uпмакс5=ЕмаксUпмакс1hмакс=1,15∙1,005∙1,172=1,354, что больше1,15.
Следовательно, необходим учет насыщения магнитопроводов.
По кривым Uнас = f(η2,Uп) (см. рис. 2.2) для Uпмакс5=1,354 и η2=0,0022 находим значение напряжения с учетом насыщения Uпнмакс5=1,335, тогда
 .
.
Математическое ожидание вынужденного напряжения на разомкнутом конце линии
 .
.
|
|
|


