 |
Глава 2. Задача о кулоновском искажении энергетического спектра СКЛ в солнечной короне
|
|
|
|
Основное уравнение, описывающее поведение функции распределения частиц по координатам и скоростям – это газокинетическое уравнение Больцмана. Однако в общем виде такое уравнение аналитического решения пока не имеет. Поэтому, как правило, вместо него используют различные приближения, основным из которых является уравнение Фоккера-Планка. В поставленной в данной работе задаче кулоновские силы, возникающие при столкновениях ионов СКЛ с частицами корональной плазмы, являются дальнодействующими, то есть основную роль играют всё же дальние взаимодействия, меняющие направление скорости ионов СКЛ на незначительный угол, нежели ближние столкновения, меняющие скорости ионов скачком. В этом случае с достаточно высокой точностью уравнение Больцмана можно заменить на уравнение Фоккера-Планка. Наверное, один из наиболее интересных выводов данного уравнения представлен в работе [15].
В данной работе предлагается ввести функцию распределения f частиц (в нашем случае ионов СКЛ), которая зависит от их радиус-вектора в фазовом пространстве Xi (xi, yi, zi, Vxi, Vyi, Vzi), где xi, yi, zi - координаты i -той частицы (иона СКЛ)), а Vxi, Vyi, Vzi - компоненты её скорости в момент времени t. Далее вводится вероятность перехода w (X, X ¢, D t) системы частиц из состояния X ¢ в состояние X за время D t. Тогда функция распределения удовлетворяет следующему интегральному уравнению Смолуховского [15]:
f (X, t + D t) = 
f (X ¢, t) w (X, X ¢, D t) d X ¢.
Перейдём в правой части от переменных X, X ¢ к переменным X ¢, D X = X ¢ − X:
f (X, t + D t) = f (X ¢, t) w (X ¢, D X, D t) d D X ¢, (2.1)
где интеграл в правой части берётся при фиксированном значении X.
Далее разложим подынтегральную функцию f в ряд Тейлора по величине D X, входящей через X ¢:
|
|
|
f (X ¢, t) w (X ¢, D X, D t) = f (X, t) w (X, D X, D t) + + 
+…
Подстановка полученного ряда в (2.1) даёт
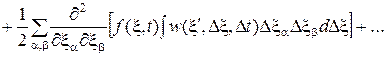(2.2)
Полученные ряды будут хорошо сходиться, если вероятность w достаточно быстро спадает с возрастанием Dξ, что и отвечает приближению непрерывного взаимодействия [3]. Это позволяет ограничиться в разложении (2.2) первыми тремя слагаемыми. Если разложить левую часть в (2.2) по степеням D t и ограничиться первым членом разложения, то получится первая форма уравнения Фоккера-Планка [15]:
, (2.3)
где
(2.4)
Уравнение (2.3) также записывают в виде:
, (2.5)
где
. (2.6)
Такая запись называется второй формой уравнения Фоккера-Планка. Коэффициенты А α образуют в такой записи вектор скорости переноса в шестимерном фазовом пространстве с координатами ξ (и называются коэффициентами динамического трения), а В αβ – тензор обобщённых коэффициентов диффузии, учитывающий как диффузию в обычном координатном пространстве, так и диффузию в пространстве скоростей. В изотропном случае тензор вырождается в скалярный коэффициент диффузии.
Уравнение (2.5), записанное в векторной форме, имеет вид:
, (2.7)
Тогда, согласно теореме Остроградского-Гаусса, величина в круглых скобках характеризует обобщённый поток в фазовом пространстве ξ. Этот факт будет в дальнейшем использован при моделировании функции распределения ионов солнечных космических лучей (метод диффузионных потоков).
Применим уравнение Фоккера-Планка (2.3) к задаче расчёта искажения энергетического спектра СКЛ под действием кулоновского взаимодействия на частицах плазмы.
Если пренебречь вторым слагаемым в (2.6), уравнение (2.7) будет записано в виде
, (2.8)
Уравнение (2.8) удобно переписать в виде
. (2.9)
Здесь
, (2.10)
- поток частиц в координатном пространстве, V -вектор скорости ионов СКЛ, c - коэффициент диффузии в координатном пространстве, а D - в скоростном, 
- ускорение ионов, возникающее за счёт кулоновского трения на частицах фоновой плазмы. В системе СИ сила кулоновского трения F имеет следующий вид [6, 7]:
|
|
|
, (2.11)
где q, m, V - заряд, масса и скорость ионов СКЛ; q b, m b, u b и n b - заряд, масса, концентрация и тепловая скорость частиц уже самой плазмы (состоящей из электронной и протонной компонент); 
– коэффициент пропорциональности из закона Кулона; l - уже упомянутый в 1 главе кулоновский логарифм (формула (1.2)).
Если считать что поток j меняется только вдоль оси Ох уравнение (2.9) примет вид
. (2.12)
При этом ось Ox мы направили вдоль основного направления движения ионов СКЛ.
Рассмотрим стационарный случай. Тогда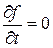 
и уравнение (2.12) примет вид
, (2.13)
Если в этом уравнении ускорение а, а также 
имеют ненулевую только х- вую компоненту, то уравнение (2.13) можно записать в виде:
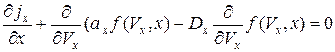, (2.14)
При этом f (Vx, x) - функция распределения частиц по Vx компоненте скорости.
В сферической системе координат в пространстве скоростей уравнение (2.10) будет выглядеть уже по-другому:
, (2.15)
В некоторых случаях велика вероятность того, что упускают из виду факт 
, то есть модуль ускорения не равен среднему темпу потери скорости ионами СКЛ. Что связано с тем, что сила кулоновского торможения не только уменьшает скорость ионов СКЛ, но и отклоняет их, при этом само отклонение может быть не связано с потерей ионами СКЛ их энергии движения. Особенно это будет заметно, если масса частиц фоновой плазмы много больше массы ионов СКЛ. При этом однозначно существует связь между потерей скорости ионов СКЛ и потерей их энергии:
, (2.16)
где 
- кулоновские потери энергии СКЛ из формулы (1.1).
Если обозначить 
, то в сферической системе координат в пространстве скоростей уравнение (2.7) примет вид
.
Данное уравнение очень часто встречается в литературе по исследованию механизмов формирования и искажения энергетического спектра ионов СКЛ. Однако в настоящей работе будет использовано уравнение Фоккера-Планка в виде соотношения (2.14) или (2.15), так как нас будет зависимость функции распределения от координаты, а не от времени.
Кроме диффузионного уравнения Фоккера-Планка в 3 главе мы также рассмотрим решение более общего, газокинетического уравнения Больцмана применительно к нашей задаче. Но для начала приведём вывод данного уравнения.
|
|
|
|
|
|
