Глава 3. Решение задачи кулоновского искажения спектра ионов СКЛ методом локального интегрирования

Если пренебречь коэффициентом диффузии как в скоростном пространстве D, так и в координатном c (то есть считаем, что распространение потока ионов СКЛ j_x сквозь корональную плазму носит конвективный характер), то уравнение (2.14) приобретёт вид

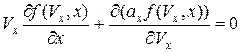. (3.1)

Сразу оговоримся, что слабость такого предположения не только в том, что не учитывается коэффициент диффузии в скоростном пространстве D, но ещё и в том, что вместо среднего темпа потери скорости (или энергии ) ионов СКЛ используется проекция их ускорения а_х на основное направление их движения. Однако на околоземной орбите регистрируются спектры именно энергий СКЛ, а не их проекций скорости. Но если считать, что распространение потока СКЛ сквозь корональную плазму, в основном, конвективное, то допущение замены на a_x оправданно. Так как в таком случае проекция и модуль скорости ионов СКЛ практически совпадают. Также нужно иметь в виду, что конвективный поток j_x = V_x f выражается через проекцию, а не модуль скорости ионов СКЛ.

В отдельных случаях это предположение оказывается наиболее сильным, например, для высокоэнергичных ионов СКЛ, которые почти наверняка имеют конвективный, а не диффузионный тип распространения. Другой возможный случай, где данное предположение может быть уместно - присутствие сильных магнитных полей. В этом случае ионы СКЛ могут распространяться на большие расстояния только вдоль силовых линий магнитного поля. И однозначно можно утверждать, что такое движение будет конвективным.

Вопрос о том, так ли на самом деле, ещё требует своего решения. Здесь стоит хотя бы упомянуть кардинальную разницу в подходах к характеру распространения (диффузионному либо конвективному) ионов СКЛ сквозь корональную плазму у разных авторов, например в работах [3] и [13].

Вернёмся однако к уравнению (3.1). Опуская индексы, перепишем его в виде

. (3.2)

Делая замену , перепишем (3.2) в виде

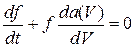
Откуда имеем

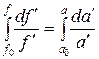
или

.

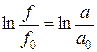Тогда решение уравнения будет иметь вид [9, 13]:

,

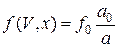где а = а (V), 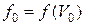‑ начальное распределение ионов СКЛ по скоростям, причём V ₀ – скорость данных частиц в начальный момент времени (то есть при x = 0), а их ускорение 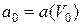. При этом V ₀ = V ₀ (V, x) находится из условия

,

Уравнение (3.2) можно решить также и стандартным способом. Введём обозначение

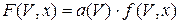, (3.3)

Тогда уравнение (3.2) запишется в виде

. (3.4)

Ищем интеграл уравнения в виде

или

. (3.5)

Тогда решение уравнения (3.4) будет иметь вид

,

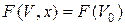или, с учётом обозначения (3.3)

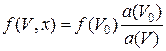, (3.6)

где V ₀ определяется из соотношения (3.5).

Если начальное распределение имеет степенной вид

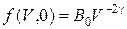[3], (3.7)

где В ₀– полученная из экспериментальных данных аппроксимирующая константа, а g ‑ экспериментально подсчитываемый показатель спектра, то решение уравнения (3.1) примет вид

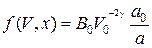, (3.8)

Основная трудность использования решения уравнения (3.2) в виде соотношения (3.8) - неберущийся интеграл (3.5), через который можно было бы выразить параметр V ₀. Поэтому воспользуемся для решения данной задачи методом локального (численного) интегрирования.

Для начала, как и в методе сеток, разделим координату х на достаточно малые интервалы Δ x = x_{i +1} − x_i, i = 1, 2… n.

Дальнейшая суть метода заключается в том, что при малом шаге интегрирования Δ x соотношение (3.5) без существенной потери точности можно записать в алгебраическом виде. Так, для х ₁ имеем

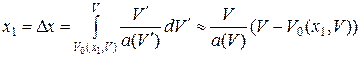, (3.9)

откуда выражаем V ₀ как

. (3.10)

И тогда согласно соотношению (3.7) имеем

.

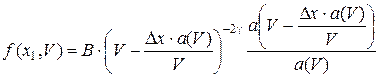По аналогии с формулой (3.9) для x ₂ имеем

,

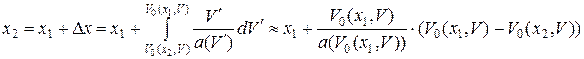Откуда для V ₀(x ₂, V) получаем (при этом имея в виду Δ x = x ₂ − x ₁):

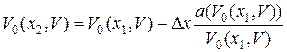. (3.11)

Обобщение формулы (3.11) даёт

.

И тогда окончательное решение уравнения (3.2) с начальным условием 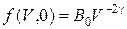, как следует из соотношения (3.8), будет иметь вид

. (3.12)

Графики для неискажённого (x = 0) и искажённого спектра, рассчитанного по соотношению (3.12) при прохождении ионами СКЛ (гелий) некоторого расстояния x = L (6,5∙10⁸ см)представлены на рис. 1 (в двойном логарифмическом масштабе).

 

	f (V, x) отн ед

Рис. 1. - График зависимости f (V, x) от скорости V для начального(неискажённого) спектра (верхний график) и искажённого спектра f (V, L) при прохождении некоторой толщи корональной плазмы L (нижний график), рассчитанный методом локального интегрирования. ue − тепловая скорость электронов.

10−9

V/ue

 

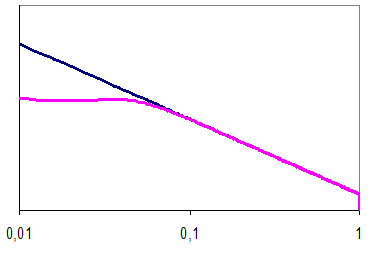
Обобщение метода

Используя результаты предыдущей задачи, попробуем теперь уже подойти к решению уравнения (2.14), более сложного и с учётом кулоновского коэффициента диффузии D в пространстве скоростей. Перепишем его ещё раз:

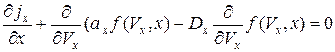, (3.13)

Считая пролёт ионами СКЛ сквозь плазму прямым, полагаем плотность потока частиц 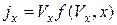. Далее, введём обозначение

.

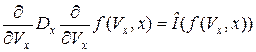И тогда, опуская индексы, уравнение (3.13) можно записать в виде

.

Вводя обозначение (3.3), перепишем его ещё раз:

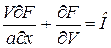. (3.14)

Считая вклад 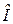в решение достаточно малым, попытаемся продвинуться в поисках данного решения, записав интеграл уравнения (3.14) как

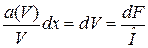. (3.15)

Вообще говоря, формула (3.15) уместна, только если 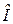положить равной константе. Однако хитрость метода численно-локального интегрирования позволяет на малом шаге интегрирования 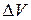действительно считать 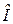примерно постоянным.

Интегрируя (3.15), получаем

,

где V₀ находится из условия (3.5).

Итак, наша задача заключается в том, чтобы найти все 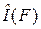и F (V, x). И, зная все F (V, x), автоматически находим f (V, x) = F (V, x)/ a (V). При этом полагаем F (V, 0) = f (V, 0) a (V) известным из начального условия (3.7).

Поделим ось Ох на достаточно малые интервалы . Тогда для F (V, x ₁) имеем

,

где V ₀ (V, x ₁) находится из соотношения (3.10).

Зная F (V, x ₁), мы автоматически знаем 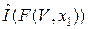. А отсюда по цепочке находим F (V, x ₂) и т.д. методом численно-локального интегрирования:

.

И таким образом находим все интересующие нас F (V, x), а значит, и f (V, x).

ВЫВОДЫ

По проделанной работе можно сделать следующие выводы:

1) Влияние силы кулоновского торможения на ионы СКЛ действительно сказывается на специфике наблюдаемой формы спектра данных ионов. А именно наблюдаются так называемые «выедания» (депрессии) в этих спектрах. При этом данные депрессии находятся примерно на одном интервале энергий для разных ионов.

2) Степень влияния силы кулоновского торможения на спектры ионов СКЛ пропорционально квадрату заряда и обратно пропорционально массе этих ионов. Также сильно зависит от пройденной толщи корональной плазмы.

3) Протонная компонента корональной плазмы вносит основной вклад в искажение энергетического спектра ионов СКЛ. Электронная компонента в торможении ионов участвует слабо.

4) Несовершенство рассмотренных моделей кулоновского искажения спектра СКЛ заключается в том, что не был учтён кулоновский коэффициент диффузии в пространстве скоростей. Учёт данного коэффициента был бы интересен в дальнейших исследованиях кулоновского искажения спектров ионов СКЛ. Другое несовершенство заключается в том, что при выводе выражения для кулоновских потерь энергий ионов СКЛ учитывались только парные столкновения, тройные столкновения и столкновения более высокого порядка не учитывались

5) В дальнейшем планируется изучить влияние других видов потерь на искажение спектра ионов СКЛ, кроме как кулоновского.

6) В задачах на кулоновское искажение спектра, как было уже продемонстрировано, одним из наиболее удобных методов расчёта оказался вышеизложенный метод локального интегрирования.

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ

1. Лытова М.Ф., Остряков В.М. Физика космической плазмы. Ускорение тяжёлых ионов: учеб. пособие; СПб. Гос. Политехн. Ун-т. - Спб.: Изд-во Политехн. Ун-та, 2006. - 108 с.

2. Кочаров Л.Г., Дворянчиков Я.В. Ускорение ионов в солнечных вспышках, богатых гелием-3. - С. 64-87.

3. Орищенко А.В., Авдонин В.В. Обогащение солнечных космических лучей изотопами и ядрами тяжёлых элементов, ДИТИ нияу мифи. ‒ М.: НИЯУ МИФИ, 2014. ‒ 131 с.

4. Кочаров Л.Г., Орищенко А.В. Механизм обогащения солнечных космических лучей тяжёлыми ионами // Известия АН СССР, сер.физ., 1984. – № 2 - С. 2162-2161.

5. Bulter S.T., M.J. Buckingham. Energy Loss of a Fast Ion in a Plasma // Physical Review, 1962. - V. 126, is. 1. – P. 1-4.

6. Трубников Б.А. Столкновения частиц в полностью ионизованной плазме. // Вопросы теории плазмы: - под ред. М.А. Леонтовича, М.: Атомиздат, 1963. - Вып.1. – С. 98-192.

7. Сивухин Д.В. Кулоновские столкновения в полностью ионизованной плазме // Вопросы теории плазмы: - под ред. М.А. Леонтовича, М.: Атомиздат, 1964. - Вып.4. - С. 81-187.

8. Korchak A.A., Coulomb Losses and the Nuclear Composition of the Solar Flare Accelerated Particles // Solar Physics: Kluwer Academic Publishers, 1972. - P. 149-281.

9. Стовпюк М.Ф. Ускорение тяжёлых ионов в солнечных вспышках и гелиосфере в рамках зарядово-согласованной модели: дис. на соискание уч. степени к-та ф.-м. наук: 01.04.02: защищена 2000. - Санкт-Петербург, 2000. - 128 с.

10. Орищенко А.В. Обогащение солнечных космических лучей тяжёлыми ионами: дис. на соискание уч. степени к-та ф.-м. наук: 01.03.02: защищена 1984. - Ленинград, 1984. - 155 с.

11. Möbius E., Scholer M., Hovestadt D., Klecker В., Gloeckler G.). Comparison of helium and heavy ion spectra in He-rich solar flares with model calculations based on stochastic Fermi acceleration in Alfven turbulence // Astrophys. J., 1982. – V.259. – P.397-410.

12. Steinacker J., Jaekel U., Schückeiser R. Ion acceleration in impulsive solar flares // Astrophys. J., 1993. – V.425. – P.342-353.

13. Картавых Ю.Ю. Стохастическое ускорение тяжёлых ионов в солнечных вспышках: кулоновские потери и изменение заряда: дис. на соискание уч. степени к-та ф.-м. наук: 01.03.02: защищена 1999. - Санкт-Петербург, 1999. - 123 с.

14. Остряков В.М., Картавых Ю.Ю., Ковальцов Г.А. Формирование энергетических спектров СКЛ при стохастическом ускорении с учётом кулоновских потерь // Письма в Астрон. Журнал, 2000. – Т. 26.

15. Франк-Каменецкий Д.А. Лекции по физике плазмы. / Д.А. Франк-Каменецкий. – М.: Атомиздат, 1968. - 287 с.

⇐ Предыдущая123

Поделиться:

Воспользуйтесь поиском по сайту: