 |
Часть III. Электричество и магнетизм
|
|
|
|
УЧЕБНО-МЕТОДИЧЕСКОЕ И ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
| Основная литература | Наличие в библиотеке университета |
| 1. Т.И.Трофимова. Курс физики. М.: Высшая школа. М. 2003-2010 | |
| 2. Т.И. Трофимова. Сборник задач по курсу физики. М. 2003-2010 | |
| Яворский и Детлаф. Курс физики | |
| Дополнительная литература | |
| 3. И.В.Савельев. Курс общей физики.Т.I. М.: Наука. 1977-1989 | |
| 4. И.В.Савельев. Курс общей физики.Т.II. М.: Наука. 1973-1988 | |
| 5. И.В.Савельев. Курс общей физики.Т.III. М: Наука. 1971-1987 |
ЧАСТЬ III. ЭЛЕКТРИЧЕСТВО и МАГНЕТИЗМ
ЭЛЕКТРОСТАТИКА
Тема 1. Теорема Остроградского-Гаусса для электростатического поля
Многие физические явления, наблюдаемые в природе и окружающей нас жизни, не могут быть объяснены только на основе законов механики, молекулярно-кинетической теории и термодинамики. В этих явлениях проявляются силы, действующие между телами на расстоянии, причем эти силы не зависят от масс взаимодействующих тел и, следовательно, не являются гравитационными. Эти силы называют электромагнитными силами.
О существовании электромагнитных сил знали еще древние греки. Но систематическое, количественное изучение физических явлений, в которых проявляется электромагнитное взаимодействие тел, началось только в конце XVIII века. Трудами многих ученых в XIX веке завершилось создание стройной науки, изучающей электрические и магнитные явления. Эта наука, которая является одним из важнейших разделов физики, получила название электродинамики.
Основными объектами изучения в электродинамике являются электрические и магнитные поля, создаваемые электрическими зарядами и токами.
Электростатическое поле – это особый вид материи, с помощью которой происходит взаимодействие заряженных тел.
|
|
|
Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.
Одним из фундаментальных законов природы является экспериментально установленный закон сохранения электрического заряда.
В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной:
|
Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака.
С современной точки зрения, носителями зарядов являются элементарные частицы. Все обычные тела состоят из атомов, в состав которых входят положительно заряженные протоны, отрицательно заряженные электроны и нейтральные частицы – нейтроны. Протоны и нейтроны входят в состав атомных ядер, электроны образуют электронную оболочку атомов. Электрические заряды протона и электрона по модулю в точности одинаковы и равны элементарному заряду e.
В нейтральном атоме число протонов в ядре равно числу электронов в оболочке. Это число называется атомным номером. Атом данного вещества может потерять один или несколько электронов или приобрести лишний электрон. В этих случаях нейтральный атом превращается в положительно или отрицательно заряженный ион.
В системе СИ элементарный заряд e равен:
| e ≈ 1,6·10–19 Кл. |
Заряд может передаваться от одного тела к другому только порциями, содержащими целое число элементарных зарядов. Таким образом, электрический заряд тела – дискретная величина:
|
Физические величины, которые могут принимать только дискретный ряд значений, называются квантованными. Элементарный заряд e является квантом (наименьшей порцией) электрического заряда. Следует отметить, что в современной физике элементарных частиц предполагается существование так называемых кварков – частиц с дробным зарядом Однако, в свободном состоянии кварки до сих пор наблюдать не удалось.
|
|
|
Точечным называется заряд, сосредоточенный на теле, размерами которого можно пренебречь по сравнению с расстоянием до других заряженных тел, с которыми он взаимодействует.
Закон Кулона:сила взаимодействия F между двумя неподвижными точечными зарядами q 1 и q 2 прямопропорциональна величинам этих зарядов и обратно пропорциональна квадрату расстояния r между ними:
,
где 
(e 0 – электрическая постоянная);
e – диэлектрическая проницаемость среды, показывающая во сколько раз сила взаимодействия зарядов в данной среде меньше, чем в вакууме.
Кулоновская сила 
направлена по прямой, соединяющей взаимодействующие точечные заряды, соответствует притяжению в случае разноименных зарядов и отталкиванию в случае одноименных зарядов.
Электрические поля, которые создаются неподвижными электрическими зарядами, называются электростатическими.
Для обнаружения и опытного исследования электростатического поля можно использовать пробный точечный заряд q 0 . Если этот заряд поместить в какую- либо точкуэлектростатического поля,то на него будетдействовать сила , величина и направление которой определяет силовую характеристику электростатического поля, носящую название напряженности электростатического поля.
Напряженность электростатического поля в данной точке есть физическая величина 
, определяемая силой, действующей на пробный точечный положительный заряд q 0 , помещенный в эту точку поля, то есть:
.
Напряжённость электростатического поля, создаваемого точечным зарядом q в любой точке поля, находящейся на расстоянии r от этого заряда:
.
Электростатическое поле может быть изображено графически с помощью силовых линий.
Силовая линия — это такая линия, касательная в каждой точке к которой совпадает по направлению с вектором напряженности электростатическго поля в данной точке (рис. 1, 2).
Рис. 1 Рис. 2
Если поле создается точечным зарядом, то силовые линии – это радиальные прямые, выходящие из положительного заряда (рис. 2, а), и входящие в отрицательный заряд (рис. 2, б).
|
|
|
С помощью силовых линий можно характеризовать не только направление, но и величину напряженности электростатического поля, связывая её с густотой силовых линий. Большей густоте силовых линий соответствует большая величина напряженности (рис. 1, 2). Количественно числу силовых линий, пронизывающих единичную площадку, расположенную перпендикулярно силовым линиям, ставится в соответствие величина напряженности электростатического поля. В этом случае определенному заряду q, создающему поле, соответствует определенное число N силовых линий, выходящих (для 
) из заряда или входящих (для 
) в заряд, а именно: 
.
Поток вектора напряженности электростатического поля через произвольную площадку S характеризуется числом силовых линий, пронизывающих данную площадку S.
Если площадка S перпендикулярна силовым линиям (рис. 3), то поток ФЕ вектора напряженности через данную площадку S: 
.
| α |
|
| S |
|
|
| S |
Рис. 3 Рис. 4
| Рис. 3 |
через данную площадку S:
,
где α – угол между векторами напряженности и нормали 
к площадке S.
| dS |
|
|
|
| α |
| S |
|
| Рис. 5 |
через произвольную поверхность S, необходиморазбить эту поверхность на элементарные площадки dS (рис. 5),определить элементарный поток dФЕ через каждую элементарную площадку dS по формуле: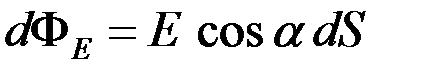 
,
а затем все эти элементарные потоки dФЕ сложить, что приводит к интегрированию:
,
| Рис. 7 |
и нормали к данной элементарной площадке dS.
Если ввести вектор 
(рис. 5) как вектор, равный по величине площади площадки dS и направленный по вектору нормали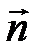 
к площадке dS, то величина 
, где a – угол между векторами и может быть записана в виде скалярного произведения векторов и , то есть, как 
, а полученное соотношение для потока вектора примет вид:
.
|
|
|
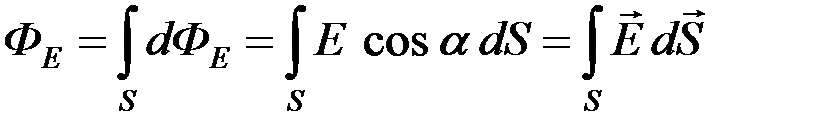Теорема Остроградского - Гаусса для электростатического поля. Теорема Остроградского - Гаусса для электростатического поля связывает между собой величину потока ФЕ вектора напряженности электростатического поля в вакууме через произвольную замкнутую поверхность S с величинойзаряда q, заключенного внутри данной замкнутой поверхности S (рис. 6).
| Рис. 6 |
| q |
| S |
|
|
) или входящие в заряд (для 
), пронизываютпроизвольную замкнутую поверхность S, охватывающую этот заряд (рис. 6), то величина потока ФЕ вектора напряженности электростатического поля через эту произвольную замкнутую поверхность S будет определяться числом N силовых линий, выходящих из заряда (для ) или входящих в заряд (для ):
.
Это соотношение есть теорема Остроградского-Гаусса дляэлектростатического поля.
Таккак поток считается положительным, если силовые линии выходят из поверхности S, и отрицательным для линий, входящих в поверхность S, то в случае, если внутри произвольной замкнутой поверхности S находится не один, а несколько (n) разноименных зарялов, то теорема Остроградского - Гаусса для электростатического поля формулируется следующим образом:
поток вектора напряженности электростатического поля в вакууме через произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на e0:
.
В общем случае электрические заряды могут быть распределены внутри объёма, ограниченного замкнутой поверхностью S, с некоторой объемной плотностью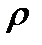 
(
), различной в разных местах пространства. Тогда суммарный заряд, заключенный внутри этой замкнутой поверхности S, охватывающей объем V,равен: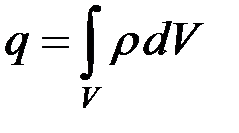 
.
В таком случае теорема Остроградского - Гаусса приобретает вид:
.
Напряженность электростатического поля зависит от диэлектрических свойств среды. В диэлектрике напряженность поля меньше, чем напряженностьвнешнего электростатического поля в вакууме, в котором находится диэлектрик, в e раз (e – диэлектрическая проницаемость среды), а модуль вектора , переходя через границу диэлектриков, скачкообразно изменяется. Поэтому для характеристики электростатического поля, кроме вектора напряженности , введен вектор электрического смещения 
, модуль которого не изменяется при переходе из одной диэлектрической среды в другую.
Вектор электрического смещения 
по определению: 
.
Используя то, что в вакууме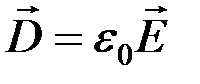 
, теорема Остроградского-Гаусса для электростатического поля может быть переформулирована следующим образом:
,
то есть поток вектора смещения электростатического поля через произвольную замкнутую поверхность S равен алгебраической сумме заключенных внутри этой поверхности зарядов.
|
|
|
В случае, если электрические заряды распределены внутри объёма V, ограни-ченного замкнутой поверхностью S, с некоторой объемной плотностью 
, теорема Остроградского-Гаусса для электростатическогополяможет быть переформулирована сдедующим образом:
.
Тема 2. Работа сил электростатического поля. Потенциал
Если в электростатическом поле, создаваемом точечным зарядом q, перемещается другой пробный заряд q 0из точки 1 в точку 2 вдоль произвольной траектории (рис. 7), то при этом совершается работа сил электростатического поля.
Элементарная работа dA силы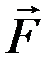 
на элементарном перемещении 
равна:
.
Из рисунка 7 видно, что 
.
Тогда 
().
| Рис. 7 |
,
то есть работа при перемещении заряда из точки 1 в точку 2 в электростатическом поле не зависит от траектории перемещения, а определяется только положениями начальной (1) и конечной (2) точек, то есть электростатическое поле точечного заряда является потенциальным.
Работа, совершаемая силами электростатического поля при перемещении заряда q 0из точки 1 в точку 2, выражается следующим образом:
,
где φ1 и φ2 – потенциалы электростатического поля в точках 1 и 2.
Потенциал электростатического поля определяется с точностью до произвольной аддитивной постоянной С, то есть для поля точечного заряда q:
.
Тогда 
, 
.
Разность потенциалов двух точек 1 и 2 в электростатическом поле определяется работой 
, совершаемой силами поля, при перемещении пробного точечного положительного заряда q 0из точки 1 в точку 2:
.
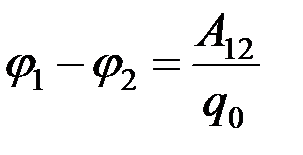Если считать, что при удалении на бесконечность потенциал электростатического поля обращается в нуль (φ∞ =0), то потенциал φ1 в данной точке поля можно определить следующим образом:
,
то есть потенциал j в данной точке поля равен работе сил электростатического поля при перемещении точечного положительного единичного заряда из данной точки поляна бесконечность.
Циркуляцией вектора напряженности электростатического поля по произвольному замкнутому контуру L называется интеграл
.
Для того, чтобы найти циркуляцию вектора напряженности по произвольному замкнутому контуру L, необходимо выбрать направление обхода контура, разбить этот контур L на элементы , для каждого элемента рассчитать величину 
(a – угол между векторами и ), а затем все эти величины сложить, что приводит к искомому интегралу.
Однако для электростатического поля циркуляция вектора напряженности по произвольному замкнутому контуру L может быть легко получена из формулы работы, совершаемой силами электростатического поля при перемещении пробного заряда q 0по произвольному замкнутому контуру L.
С одной стороны, эта работа равна:
,
а с учетом того, что 
эта работа равна:
.
С другой стороны, эта работа может быть определена с помощью формулы:
,
из которой следует, что для произвольного замкнутого контура эта работа равна нулю, так как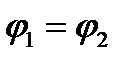 
. Тогда и циркуляция вектора по произвольному замкнутому контуру L тоже равна нулю, то есть:
.
Величина 
, где a – угол между векторами и может быть записана в виде скалярного произведения векторов и , то есть, как 
, а полученное соотношение для циркуляции вектора примет вид:
.
Полученное соотношение является признаком потенциального силового поля. Обращение в нуль циркуляции вектора означает, что силовые линии электростатического поля не являются замкнутыми, они начинаются и заканчиваются на зарядах (соответственно на положительных или отрицательных) или же уходят в бесконечность, что также является свойством потенциального силового поля.
Связь между напряженностью и потенциалом электростатического поля
Напряженность и потенциал φ электростатического поля связаны между собой следующим образом:
= – grad φ или 
, где
– единичные векторы координатных осей Ох, Оy, Оz, соответственно.
Знак минус в приведенной формуле означает, что вектор напряженности электростатического поля направлен в сторону максимального убывания потенциала j.
Для графического изображения распределения потенциала электростатического поля используются эквипотенциальные поверхности, то естьповерхности, во всех точках которых потенциал j имеет одно и то же значение.
| Рис. 8 |
Например, для поля, созданного точечным зарядом q, потенциал j определяется выражением: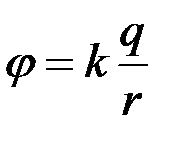 
, а эквипотенциальными поверхностями являются концентрические сферы (рис. 8). Из этого рисунка видно, что в случае точечного заряда силовые линии поля (штриховые линии) нормальны к эквипотенциальным поверхностям.
Это свойство нормального взаимного расположения силовых линий и эквипотенциальных поверхностей поля является общим для любых случаев электростатического поля. То есть, зная расположение силовый линий электростатического поля, можно построить эквипотенциальные поверхности и, наоборот, по известному расположению эквипотенциальных поверхностей можно построить силовые линии электростатического поля.
|
|
|
