 |
Уравнение свободных незатухающих гармонических колебаний.
|
|
|
|
Для возбуждения в контуре колебаний предварительно заряжают конденсатор, сообщая его обкладкам заряд ±q. Тогда в начальный момент времени t= 0 (рис. 19, а) между обкладками конденсатора возникнет электрическое поле. Если замкнуть конденсатор на катушку индуктивности, конденсатор начнет разряжаться, и в контуре потечет возрастающий со временем ток I. Когда конденсатор полностью разрядится, энергия электрического поля конденсатора полностью перейдет в энергию магнитного поля катушки (рис. 19, б). Начиная с этого момента ток в контуре будет убывать, и, следовательно, начнет ослабевать магнитное поле катушки, тогда в ней согласно закону Фарадея индуцируется ток, который течет в соответствии с правилом Ленца в том же направлении, что и ток разрядки конденсатора. Конденсатор начнет перезаряжаться, возникнет электрическое поле, стремящееся ослабить ток, который, в конце концов, обратится в нуль, а заряд на обкладках конденсатора достигнет максимума (рис. 19, в). Далее те же процессы начнут протекать в обратном направлении (рис. 19, г), и система к моменту времени t=Т (Т – период колебаний) придет в первоначальное состояние (рис. 19, а). После этого начнется повторение рассмотренного цикла разрядки и зарядки конденсатора, то есть начнутся периодические незатухающие колебания величины заряда q на обкладках конденсатора, напряжения UC на конденсаторе и силы тока I, текущего через катушку индуктивности. Согласно закону Фарадея напряжение UC на конденсаторе определяется скоростью изменения силы тока в катушке индуктивности идеального контура, то есть:
.
Исходя из того, что UC=q/C, а I=dq/dt, получаем дифференциальное уравнение свободных незатухающих гармонических колебаний величины заряда q на обкладках конденсатора:
|
|
|
или 
.
Решением этого дифференциального уравнения является функция q (t), то есть уравнение свободных незатухающих гармонических колебаний величины заряда q на обкладках конденсатора:
,
где q (t) – величина заряда на обкладках конденсатора в момент времени t;
q 0 – амплитуда колебаний заряда на обкладках конденсатора;
– круговая (или циклическая) частота колебаний (
);
=2 
/ T (T – период колебаний, 
– формула Томсона);
– фаза колебаний в момент времени t;
– начальная фаза колебаний, то есть фаза колебаний в момент времени t =0.
Уравнение свободных затухающих гармонических колебаний. В реальном колебательном контуре учитывается, что кроме катушки индуктивностью L, конденсатора емкостью С, в цепи также имеется резистор сопротивлением R,отличным от нуля, что является причиной затухания колебаний в реальном колебательном контуре. Свободные затухающие колебания – колебания, амплитуда которых из-за потерь энергии реальной колебательной системой с течением времени уменьшается.
Для цепи реального колебательного контура напряжения на последовательно включенных конденсаторе емкостью С и резисторе сопротивлением R складываются. Тогда с учетом закона Фарадея для цепи реального колебательного контура можно записать:
,
где 
– электродвижущая сила самоиндукции в катушке;
UC – напряжение на конденсаторе (UC =q/C);
IR – напряжения на резисторе.
Исходя из того, что I=dq/dt, получаем дифференциальное уравнение свободных затухающих гармонических колебаний величины заряда q на обкладках конденсатора:
или 
,
где 
– коэффициент затухания колебаний (
), 
.
Решением полученного дифференциального уравнения является функция q (t), то есть уравнение свободных затухающих гармонических колебаний величины заряда q на обкладках конденсатора:
,
где q (t) – величина заряда на обкладках конденсатора в момент времени t;
|
|
|
– амплитуда затухающих колебаний заряда в момент времени t;
q 0 – начальная амплитуда затухающих колебаний заряда;
– круговая (или циклическая) частота колебаний (
);
– фаза затухающих колебаний в момент времени t;
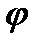– начальная фаза затухающих колебаний.
Период свободных затухающих колебаний в реальном колебательном контуре:
.
Вынужденные электромагнитные колебания. Чтобы в реальной колебательной системе получить незатухающие колебания, необходимо в процессе колебаний компенсировать потери энергии. Такая компенсация в реальном колебательном контуре возможна с помощью внешнего периодически изменяющегося по гармоническому закону переменного напряжения U (t):
.
В этом случае дифференциальное уравнение вынужденных электромагнитных колебаний примет вид:
или 
.
Решением полученного дифференциального уравнения является функция q (t):
.
В установившемся режиме вынужденные колебания происходят с частотой w и являются гармоническими, а амплитуда 
и фаза колебаний 
определяются следующими выражениями:
; 
.
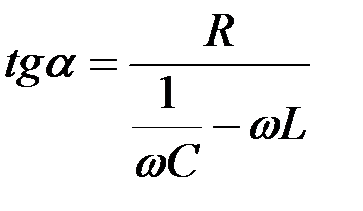Отсюда следует, что амплитуда колебаний величины заряда имеет максимум при резонансной частоте внешнего источника 
:
.
Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающего переменного напряжения к частоте, близкой частоте 
, называется резонансом.
Тема 10. Электромагнитные волны
Согласно теории Максвелла электромагнитные поля могут существовать в виде электромагнитных волн, фазовая скорость 
распространения которых определяется выражением:
,
где 
и 
– соответственно электрическая и магнитная постоянные,
e и m – соответственно электрическая и магнитная проницаемости среды,
с – скорость света в вакууме (
).
В вакууме (e = 1, m = l) скорость распространения электромагнитных волн совпадает со скоростью света(с), что согласуется с теорией Максвелла о том,
что свет представляет собой электромагнитные волны.
По теории Максвелла электромагнитные волны являются поперечными, то есть векторы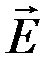 
и 
напряженностей электрического и магнитного полей взаимно перпендикулярны и лежат в плоскости, перпендикулярной вектору 
|
|
|
скорости распространения волны, причем векторы 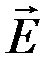, и образуют правовинтовую систему (рис. 20).
|
|
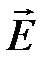
| x |
| у |
| z |
|
| Рис. 20 |
Из теории Максвелла следует также, что в электромагнитной волне векторы 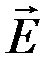и колеблются в одинаковых фазах (рис. 20), то есть значения напряженностей Е и Н электрического и магнитного полей одновременно достигают максимума и одновременно обращаются в нуль, причем мгновенные значения Е и Н связаны соотношением: 
.
Уравнение плоской монохроматической электромагнитной волны (индексы у и z при Е и Н подчеркивают лишь то, что векторы 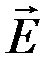и направлены вдоль взаимно перпендикулярных осей в соответствии с рис. 20):
,
,
где E 0 и Н 0– соответственно амплитуды напряженностей электрического и магнитного полей,
w – круговая частота волны, 
(T – период колебаний),
k – волновое число, 
(
– длина волны),
j – начальная фаза колебаний (начальная фаза колебаний j имеет одинаковое значение как для колебания электрического, так и магнитного векторов, так как в электромагнитной волне эти колебания происходят в одинаковых фазах).
Энергия электромагнитных волн. Электромагнитные волны переносят энергию. Объемная плотность w энергии электромагнитной волны складывается из объемных плотностей wэл электрического и wм магнитного полей:
.
Учитывая выражение связи между величинами Е и Н, можно получить, что суммарная плотность энергии электрического и магнитного полей:
.
Умножив плотность энергии w на скорость 
распространения волны в среде, получим модуль плотности потока энергии:
.
Tax как векторы 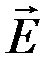и взаимно перпендикулярны, то произведение EH совпадает с модулем вектора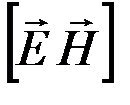 
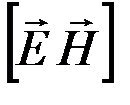( – векторное произведение векторов 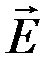и 
). Кроме того, направление вектора 
совпадает с направлением распространения волны, то есть с направлением переноса энергии, что позволило ввести в ектор 
, равныйвекторному произведению , как вектор плотности потока электромагнитной энергии, называемый вектором Умова – Пойнтинга:
.
Итак, вектор 
направлен в сторону распространения электромагнитной волны, а его модуль равен энергии, переносимой электромагнитной волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны.
|
|
|
|
|
|
