Соответственно мощность, выделяемая в цепи, определяется по формуле

. (7.14)

Энергия, выделяемая в цепи постоянного тока, может расходоваться:

– на выделение теплоты (например, спираль электроплиты при пропускании тока нагревается);

– совершение механической работы (например, ротор электродвигателя при протекании по нему тока вращается);

– совершение химических превращений (например, при зарядке аккумулятора);

– свечение (например, лампы дневного света при подаче на них напряжения);

– генерацию акустических волн (например, в электродинамиках) и т. д.

В случае, когда проводник неподвижен и химических превращений в нем не совершается, работа тока [формула (7.13)] затрачивается на увеличение внутренней энергии проводника, в результате чего проводник нагревается. При протекании тока в проводнике выделяется теплота

.

Заменив в (7.13) в соответствии с законом Ома , получим формулу

. (7.15)

Соотношение (7.15) было установлено экспериментально в 1841 г. английским физиком Д. Джоулем и независимо от него в 1842 г. русским ученым Э. Х. Ленцем и

носит название закона Джоуля–Ленца: количество теплоты, выделяющейся в единицу времени на участке цепи, при протекании по нему постоянного тока, равно произведению сопротивления участка цепи на квадрат силы тока.

 

Поскольку величины, фигурирующие в формуле (7.15), являются интегральными (характеризующими проводник конечных размеров), то можно сказать, что выражение (7.15) описывает закон Джоуля–Ленца в интегральной форме.

От формулы (7.15), определяющей теплоту, выделяющуюся во всем проводнике, можно перейти к выражению, характеризующему выделение теплоты в различных местах проводника. Выделим в проводнике таким же образом, как это было сделано при выводе формулы (7.9), элементарный объем в виде цилиндра (см. рис. 7.1). Согласно закону Джоуля–Ленца за время в этом объеме выделится теплота

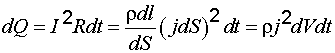, (7.16)

где – элементарный объем.

Разделив выражение (7.16) на и , найдем количество теплоты, выделяющееся в единице объема в единицу времени, – удельную тепловую мощность тока:

. (7.17)

Используя дифференциальную форму закона Ома [формула (7.9)] и соотношение , получим

. (7.18)

Формула (7.18) представляет собой дифференциальную форму закона Джоуля–Ленца.

Отметим, что Джоуль и Ленц установили свой закон для однородного участка цепи. Однако, как следует из выкладок, приведенных в данном параграфе, формулы (7.15) и (7.18) справедливы и для неоднородного участка при условии, что действующие в нем сторонние силы имеют нехимическое происхождение.

§ 5. Разветвленные цепи. Правила Кирхгофа

Расчет разветвленных электрических цепей значительно упрощается, если пользоваться правилами, сформулированными Кирхгофом. Этих правил два. Первое из них относится к узлам цепи. Узлом называется точка, в которой сходятся более чем два проводника (рис. 7.3). При этом ток, входящий в узел, считается положительным, а ток, выходящий из узла – отрицательным. Первое правило Кирхгофа гласит, что алгебраическая сумма токов, сходящихся в узле, равна нулю: .(7.19)

Например (рис. 7.3), первое правило Кирхгофа запишется так:

.

Первое правило вытекает из закона сохранения электрического заряда.

В случае установившегося постоянного тока ни в одной точке проводника не должны накапливаться электрические заряды. В противном случае токи не могли бы оставаться постоянными.

Уравнение (7.19) можно написать для каждого из N узлов цепи. Однако независимыми являются только N – 1 уравнений, N-e будет следствием из них.

Второе правило относится к любому выделенному в разветвленной цепи замкнутому контуру (например, контур АВС на рис. 7.4). Зададим направление обхода (например, по часовой стрелке, на ри­с. 7.4). Если направление совпадает с направлением обхода контура, то ток считается положительным, а если не совпадает, – отрицательным. Применим к каждому из неразветвленных участков контура закон Ома:

При сложении этих выражений потенциалы взаимно уничтожаются и получается уравнение

,

которое выражает второе правило Кирхгофа: в любом замкнутом контуре, произвольно выбранном в разветвленной цепи, алгебраическая сумма произведений сил токов на сопротивления соответствующих участков этого контура равна алгебраической сумме эдс , встречающихся в этом контуре:

. (7.20)

Уравнение (7.20) может быть составлено для всех замкнутых контуров, которые можно выделить мысленно в данной разветвленной цепи. Однако независимыми будут только уравнения для тех контуров, которые нельзя получить наложением других контуров один на другой.

При составлении уравнений второго правила Кирхгофа токам и эдс нужно приписывать знаки в соответствии с выбранным направлением обхода. Эдс также нужно приписать знак минус, так как она действует в направлении, противоположном направлению обхода. Направления обхода в каждом из контуров можно выбирать совершенно произвольно и независимо от выбора направлений в других контурах. При этом может случиться, что один и тот же ток либо одна и та же эдс войдет в разные уравнения с различными знаками. Это, однако, не имеет никакого значения, потому что изменение направления обхода вызывает лишь изменение всех знаков в уравнении (7.20) на обратные.

Число независимых уравнений, составленных в соответствии с первым и вторым правилами Кирхгофа, оказывается равным числу различных токов, текущих в разветвленной цепи. Поэтому, если заданы эдс и сопротивления для всех неразветвленных участков, то могут быть вычислены все токи.

 

 

Магнитное поле

Тема 3. Магнитное поле. Закон Био-Савара-Лапласа

Электрический ток создает поле, действующее на магнитную стрелку. Стрелка ориентируется по касательной к окружности, лежащей в плоскости, перпендикуляной к проводнику с током (рис. 9).

Основной характеристикой магнитного поля является вектор индукция . Принято, что вектор индукция магнитного поля направлен в сторону север-ного полюса магнитной стрелки, помещенной в данную точку поля (рис. 9).

По аналогии с электрическим полем, магнитное поле также может быть изображено графически с помощью силовых линий (линий индукции магнитного поля).

Силовая линия – это такая линия, касательная к которой в каждой точке совпадает по направлению с вектором индукции магнитного поля. Силовые линии магнитного поля, в отличие от силовых линий электростатического поля, являются замкнутыми и охватывают проводники с током. Направление силовых линий задается правилом правого винта (правилом буравчика): головка винта, ввинчиваемого по направлению тока, враща­ется в направлении линий магнитной индукции (рис. 9).

I

N

S

 

 

Рис. 9

Для нескольких источников магнитного поля согласно принципу суперпозиции магнитных полей индукция результирующего магнитного поля равна векторной сумме индукций всех отдельных магнитных полей:

.

Вектор индукции магнитного поля, создаваемого проводником с током , можно определить с помощью закона Био-Савара-Лапласа. При этомнеобходимо учесть то, что закон Био-Савара-Лапласа позволяет найти модуль и направление лишьвектора индукции магнитного поля, создаваемого элементом проводника с током . Поэтому, для определения вектора индукции магнитного поля, создаваемого проводником с током , необходимо первоначально разбить этот проводник на элементы проводника , для каждого элемента с помощью закона Био-Савара-Лапласа найти вектор индукции , а затем, используя принцип суперпозиции магнитных полей, сложить векторно все найденные вектора индукции .

Закон Био-Савара-Лапласа в векторной форме:

I

М

Рис. 10

α

,

где – индукция магнитного поля в точке M, заданной радиусом-вектором , проведенным от начала вектора 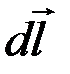до этой точки;

– векторное произведение векторов и ;

– магнитная постоянная,

– магнитная проницаемость среды.

Направление вектора 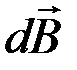определяется по правилу правого винта: направление враще­ния головки винта дает направление вектора 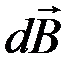, если поступательное движение винта совпадает с направлением тока в элементе проводника (рис. 10).

В скалярном виде закон Био-Савара-Лапласа:

, где – угол между векторами 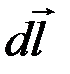и .

Магнитное поле линейного тока. Для нахождения индукции магнитного поля, созданного прямым проводником с током (рис. 11), необходимо разбить весь проводник на элементы 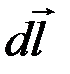, для каждого элемента проводника 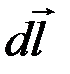с током I найти вектор индукции , а затем векторно сложить все найденные .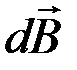

В произвольной точке М, удаленной от оси проводника на расстояние b (рис. 11), векторы 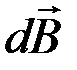от всех элементов проводника 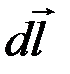с током I имеют одинаковое направление, перпендикулярное плоскости чертежа («к нам»). Поэтому сложение векторов 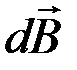можно заменить сложением их модулей.

I

α

D

а

b

М

С

О

Рис. 11

 

 

По закону Био-Савара-Лапласа модуль вектора магнитной индукции 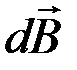в точке М поля, созданного элементом проводника 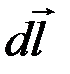с током I:

.

В качестве переменной интегрирования выберем угол , выразив через этот угол все остальные величины.

Из рисунка 11 следует, что , а с другой стороны, .

Тогда , а модуль вектора магнитной индукции 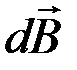в точке М:

.

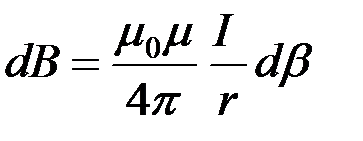Из прямоугольного треугольника DOM:

, откуда .

Следовательно, индукция dB, создаваемая элементом проводника dl с током I:

.

Теперь можно перейти к интегрированию:

.

Так как угол для прямого тока изменяется в пределах от до , то магнитная индукция поля прямого тока:

.

Следовательно,

.

Магнитное поле в центре кругового проводника с током. Для нахождения индукции магнитного поля в центре кругового проводника с током необходимо разбить этот проводник на элементы 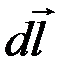, причем все элементы проводника с током создают в центре кругового тока магнитные поля одинакового направления – вдоль нормали к плоскости витка (рис. 12). Поэтому сложение век­торов 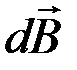можно заменить сложением их модулей dB.

По закону Био-Савара-Лапласа модуль вектора :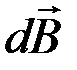

.

Так как все элементы 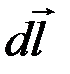проводника перпендикулярны соответствующим радиусам-векторам (рис. 12), то sin a = 1 для всех элементов 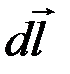. Расстояния r для всех элементов проводника 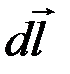также одинаковые (r = R).

Тогда выражение для модуля вектора 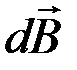примет вид:

.

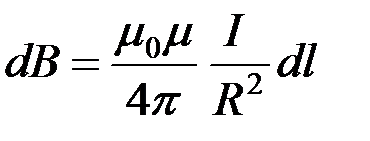Теперь для нахождения модуля вектора 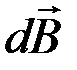можно перейти к интегрированию:

.

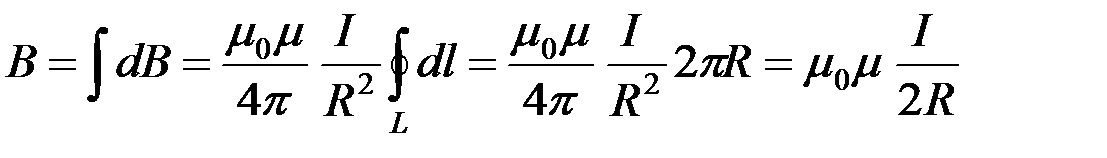Следовательно, индукция магнитного поля B в центре кругового проводника радиусом R с током I:

.

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: