 |
Дирекционные углы и осевые румбы
|
|
|
|
Осевой (средний) истинный меридиан зоны часто принимают за основное направление. В этом случае положение линии местности относительно осевого меридиана определяет угол ориентирования, называемый дирекционным (рис. 16).
Дирекционный угол измеряется от северного направления осевого меридиана в направлении движения часовой стрелки через восток, юг и запад. Следовательно, градусная величина дирекционного угла может иметь любое значение от 0° до 360°.
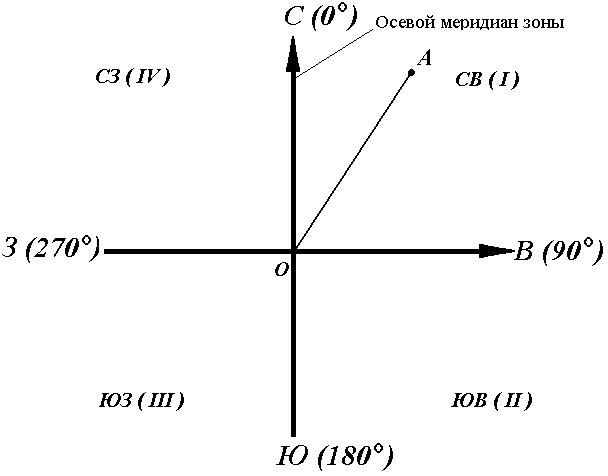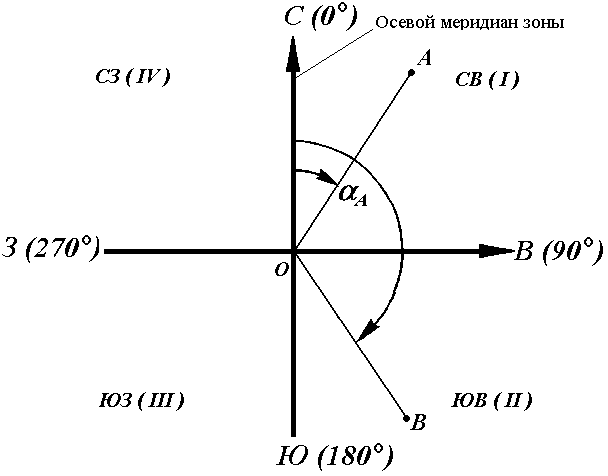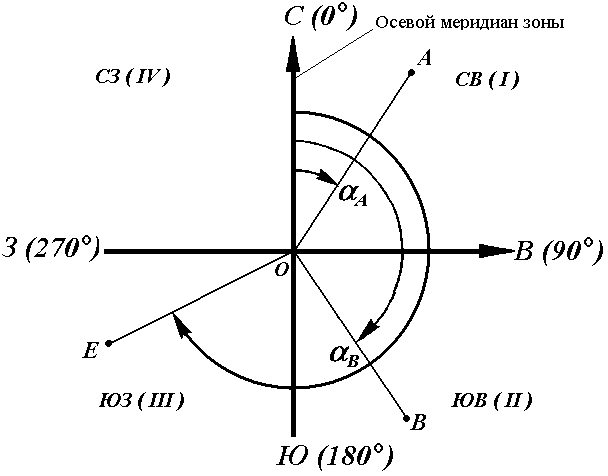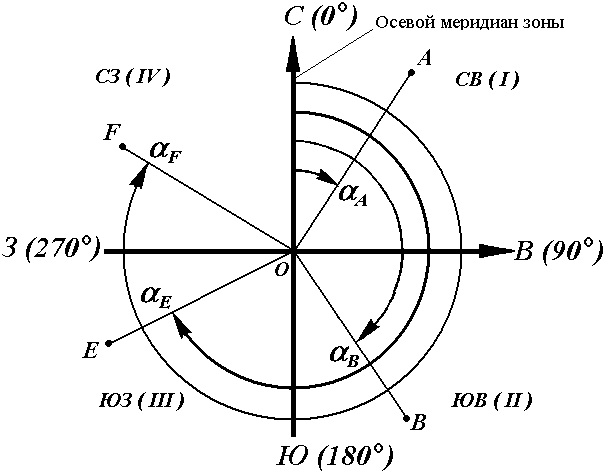
Рис. 16. Дирекционные углы
Для линии ОА её дирекционным углом в точке О является горизонтальный угол αОA между северным направлением осевого меридиана и направлением линии. Для линий ОВ, ОЕ и ОF – αОВ, αОE, αОF.
Таким образом, дирекционным углом является угол в горизонтальной плоскости, отсчитываемый от северного направления осевого меридиана по ходу часовой стрелки до данной линии.
В геодезии принято различать прямое и обратное направление линии (рис. 17). Так, если ВС считать прямым направлением линии, то СВ будет обратным направлением той же линии. В соответствии с этим αBC является прямым дирекционным углом линии ВС в точке М, а угол αCB – обратным дирекционным углом этой же линии в той же точке.

Рис. 17. Прямое и обратное направление линии
Из рисунка видно, что αCB = αBC + 180°, т.е. прямой и обратный дирекционные углы отличаются друг от друга на 180°.
Иногда для ориентирования линии местности пользуются не дирекционными углами, а румбами (рис. 18).
Осевым румбом называется острый горизонтальный угол, отсчитываемый от ближайшего направления осевого меридиана (северного или южного) до данной линии. Румбы обозначают буквой r с индексом, указывающим четверть, в которой находится румб.
|
|
|
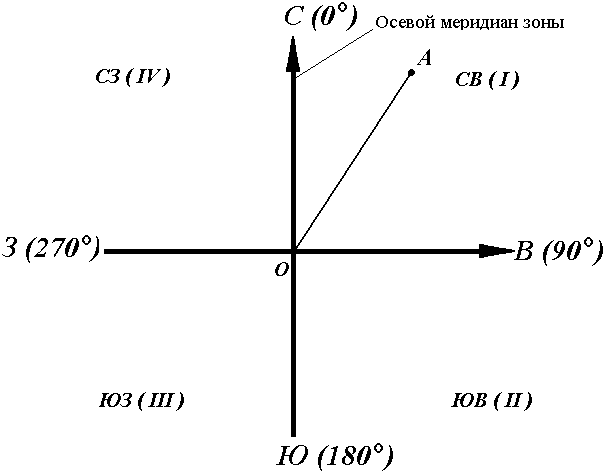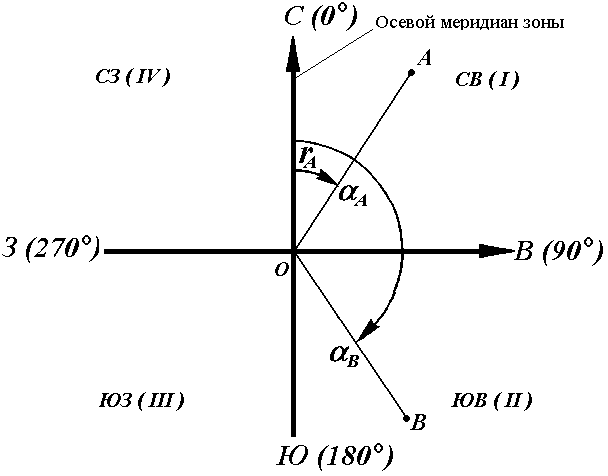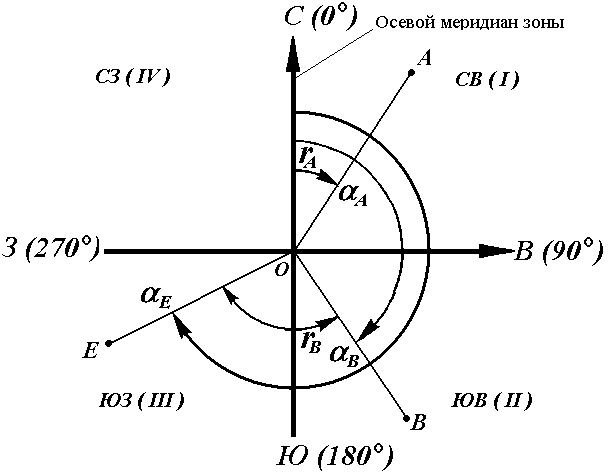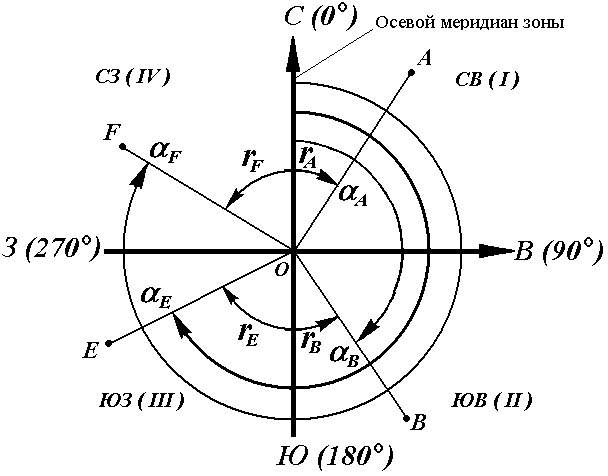
Рис. 18. Румбы и дирекционные углы
Название четвертей составлены из соответствующих обозначений главных точек горизонта: север (С), юг (Ю), восток (В), запад (З).
Зависимость между дирекционными углами и румбами определяется для четвертей по следующим формулам:
I четверть (СВ) r = α
II четверть (ЮВ) r = 180° – α
III четверть (ЮЗ) r = α – 180°
IV четверть (СЗ) r = 360° – α
Румб в точке М направления ВС называется прямым, а противоположного направления СВ – обратным. Прямой и обратный румб в одной и той же точке данной линии равны по численному значению, но имеют индексы противоположных четвертей.
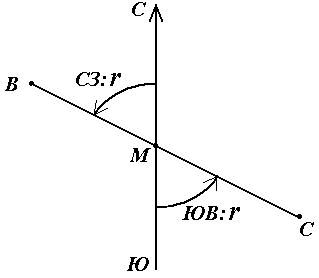
Рис. 19. Прямой и обратный румбы
Истинные азимуты и румбы
Кроме осевого меридиана зоны при ориентировании линий местности за основное направление может приниматься направление истинного (географического) меридиана.
Истинный меридиан – линия пересечения земной поверхности с плоскостью, проходящей через отвесную линию и ось вращения Земли.
Положение линии местности относительно истинного меридиана определяется истинным азимутом или истинным румбом.
Истинный азимут линии – угол в горизонтальной плоскости, отсчитываемый от северного направления истинного меридиана по ходу часовой стрелки до данной линии (рис. 20).
Истинный румб линии – острый горизонтальный угол, отсчитываемый от ближайшего направления истинного меридиана (северного или южного) до данной линии.

Рис. 20. Истинные азимутыы
Истинный азимут A измеряется от 0° до 360°. Зависимость между истинными азимутами и румбами такая же, как и между дирекционными углами и осевыми румбами.
Истинные меридианы, проходящие через точки Земли с разной долготой, не параллельны между собой и сходятся на полюсах. Поэтому азимуты одной и той же прямой линии, определяемые относительно разных истинных меридианов, отличаются на величину γ (рис. 21), которую называют углом сближения меридианов. Его приближенное значение можно рассчитать по формулам:
|
|
|
γ = 0,54 · l · tg φ или γ = sin φ · Δλ,
где l – длина прямой линии между точками (км); φ – средняя широта линии; Δλ – разность долгот. При l = 1 км и широте Хабаровска φ = 48°28' угол сближения меридианов γ = 0,6' = 36".

Рис. 21. Зависимость между истинным азимутом и дирекционным углом
Для перехода от дирекционного угла к истинному азимуту и наоборот необходимо знать угол сближения γ между осевым и истинным меридианом (рис. 21). Зависимость между истинным азимутом и дирекционным углом следующая
А = α + γ.
Если точка расположена к западу от осевого меридиана, то величину угла сближения γ между осевым и истинным меридианом принято считать отрицательной, если к востоку – положительной (рис. 21). Например, истинные азимуты линии при дирекционном угле α = 70° и углах сближения γ = – 0°50' для западной точки М1, γ = 0°50' для восточной – М2 соответственно равны
А1 = 70° – 0°50' = 69°50',
А2 = 70° + 0°50' = 70°50'.
Магнитные азимуты и румбы
При ориентировании линий местности за основное направление может также приниматься направление магнитного меридиана.
Магнитная стрелка на концах имеет точки, в которых сосредоточены магнитные массы. Соединяющая их линия называется магнитной осью стрелки.
Вертикальная плоскость, проходящая через магнитную ось стрелки, является плоскостью магнитного меридиана.
Линия пересечения плоскости магнитного меридиана с горизонтальной плоскостью дает направление магнитного меридиана.
Горизонтальный угол, отсчитываемый от северного направления магнитного меридиана по ходу часовой стрелки до данной линии, называется магнитным азимутом Ам (рис. 22).

Рис. 22. Магнитный азимут и склонение магнитной стрелки: а) западное; б) восточное
В каждой точке на поверхности Земли магнитный и истинный меридианы образуют между собой угол, называемый склонением магнитной стрелки δ (рис. 22). Северный конец магнитной стрелки может отклоняться от истинного меридиана к западу или востоку. В зависимости от этого различают западное и восточное склонения. Восточное склонение принято считать положительным, западное – отрицательным:
|
|
|
Аи = Ам + δвост,
Аи = Ам – δзап.
Магнитное склонение в разных пунктах Земли различно и непостоянно. Различают вековые, годовые и суточные изменения склонения. В связи с этим магнитная стрелка указывает направление магнитного меридиана приблизительно и ориентировать линию по нему можно только тогда, когда не требуется большая точность ориентирования.
|
|
|


