 |
Рельеф. Основные формы рельефа
|
|
|
|
Рельеф – форма физической поверхности Земли, рассматриваемая по отношению к её уровенной поверхности.
Рельефом называется совокупность неровностей суши, дна океанов и морей, разнообразных по очертаниям, размерам, происхождению, возрасту и истории развития. При проектировании и строительстве железных, автомобильных и других сетей необходимо учитывать характер рельефа – горный, холмистый, равнинный и др.
Рельеф земной поверхности весьма разнообразен, но все многообразие форм рельефа для упрощения его анализа типизировано на небольшое количество основных форм (рис. 29).

Рис. 29. Формы рельефа:
1 — лощина; 2 — хребет; 3, 7, 11 — гора; 4 — водораздел; 5, 9 — седловина; 6 — тальвег; 8 — река; 10 — обрыв; 12 — терраса
К основным формам рельефа относятся:
Гора – это возвышающаяся над окружающей местностью конусообразная форма рельефа. Наивысшая точка её называется вершиной. Вершина может быть острой – пик, или в виде площадки – плато. Боковая поверхность состоит из скатов. Линия слияния скатов с окружающей местностью называется подошвой или основанием горы.
Котловина – форма рельефа, противоположная горе, представляющая собой замкнутое углубление. Самая низкая точка её – дно. Боковая поверхность состоит из скатов; линия их слияния с окружающей местностью называется бровкой.
Хребет – это возвышенность, вытянутая и постоянно понижающаяся в каком – либо направлении. У хребта два склона; в верхней части хребта они сливаются, образуя водораздельную линию, или водораздел.
Лощина – форма рельефа, противоположная хребту и представляющая вытянутое в каком – либо направлении и открытое с одного конца постоянно понижающееся углубление. Два ската лощины; сливаясь между собой в самой низкой части её образуют водосливную линию или тальвег, по которой стекает вода, попадающая на скаты. Разновидностями лощины являются долина и овраг: первая является широкой лощиной с пологими задернованными скатами, вторая – узкая лощина с крутыми обнаженными скатами. Долина часто бывает ложем реки или ручья.
|
|
|
Седловина – это место, которое образуется при слиянии скатов двух соседних гор. Иногда седловина является местом слияния водоразделов двух хребтов. От седловины берут начало две лощины, распространяющиеся в противоположных направлениях. В горной местности через седловины обычно пролегают дороги или пешеходные тропы; поэтому седловины в горах называют перевалами.
3.3. Изображение рельефа на планах и картах
Для решения инженерных задач изображение рельефа должно обеспечивать: во-первых, быстрое определение с требуемой точностью высот точек местности, направления крутизны скатов и уклонов линий; во-вторых, наглядное отображение действительного ландшафта местности.
Рельеф местности на планах и картах изображают различными способами (штриховкой, пунктиром, цветной пластикой), но чаще всего с помощью горизонталей (изогипсов), числовых отметок и условных знаков.
Горизонталь на местности можно представить как след, образованный пересечением уровенной поверхности с физической поверхностью Земли. Например, если представить холм, окружённый неподвижной водой, то береговая линия воды и есть горизонталь (рис. 30). Лежащие на ней точки имеют одинаковую высоту.
Допустим, что высота уровня воды относительно уровенной поверхности 110 м (рис. 30). Предположим теперь, что уровень воды упал на 5 м и часть холма обнажилась. Кривая линия пересечения поверхностей воды и холма будет соответствовать горизонтали с высотой 105 м. Если последовательно снижать уровень воды по 5 м и проектировать кривые линии, образованные пересечением поверхности воды с земной поверхностью, на горизонтальную плоскость в уменьшенном виде, то получим изображение рельефа местности горизонталями на плоскости.
|
|
|
Таким образом кривая линия, соединяющая все точки местности с равными отметками, называется горизонталью.

Рис. 30. Способ изображения рельефа горизонталями
При решении ряда инженерных задач необходимо знать свойства горизонталей:
1. Все точки местности, лежащие на горизонтали, имеют равные отметки.
2. Горизонтали не могут пересекаться на плане, поскольку они лежат на разных высотах. Исключения возможны в горных районах, когда горизонталями изображают нависший утес.
3. Горизонтали являются непрерывными линиями. Горизонтали, прерванные у рамки плана, замыкаются за пределами плана.
4. Разность высот смежных горизонталей называется высотой сечения рельефа и обозначается буквой h.
Высота сечения рельефа в пределах плана или карты строго постоянна. Её выбор зависит от характера рельефа, масштаба и назначения карты или плана. Для определения высоты сечения рельефа иногда пользуются формулой
h = 0,2 мм · М,
где М – знаменатель масштаба.
Такая высота сечения рельефа называется нормальной.
5. Расстояние между соседними горизонталями на плане или карте называется заложением ската или склона. Заложение есть любое расстояние между соседними горизонталями (см. рис. 30), оно характеризует крутизну ската местности и обозначается d.
Вертикальный угол, образованный направлением ската с плоскостью горизонта и выраженный в угловой мере, называется углом наклона ската ν (рис. 31). Чем больше угол наклона, тем круче скат.
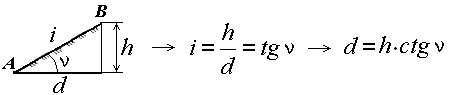
Рис. 31. Определение уклона и угла наклона ската
Другой характеристикой крутизны служит уклон i. Уклоном линии местности называют отношение превышения к горизонтальному проложению. Из формулы следует (рис. 31), что уклон безразмерная величина. Его выражают в сотых долях (%) или тысячных долях – промиллях (‰).
Если угол наклона ската до 45°, то он изображается горизонталями, если его крутизна более 45°, то рельеф обозначают специальными знаками. Например, обрыв показывается на планах и картах соответствующим условным знаком (рис. 32).
|
|
|
Изображение основных форм рельефа горизонталями приведено на рис. 32.

Рис. 32. Изображение форм рельефа горизонталями
Для изображения рельефа горизонталями выполняют топографическую съемку участка местности. По результатам съемки определяют координаты (две плановые и высоту) для характерных точек рельефа и наносят их на план (рис. 33). В зависимости от характера рельефа, масштаба и назначения плана выбирают высоту сечения рельефа h.

Рис. 33. Изображение рельефа горизонталями
Для инженерного проектирования обычно h = 1 м. Отметки горизонталей в этом случае будут кратны одному метру.
Положение горизонталей на плане или карте определяется с помощью интерполирования. На рис. 33 приведено построение горизонталей с отметками 51, 52, 53, 54, 55, 56, 57 м. Горизонтали кратные 5 или 10 м проводят на чертеже утолщенными и подписывают. Подписи наносят таким образом, чтобы верх цифр указывал сторону повышения рельефа. На рис. 33 подписана горизонталь с отметкой 55 м.
Там, где заложения больше, наносят штриховые линии (полугоризонтали). Иногда, чтобы сделать чертеж более наглядным, горизонтали сопровождают небольшими черточками, которые ставятся перпендикулярно горизонталям, по направлению ската (в сторону стока воды). Эти черточки называются бергштрихи.
Цифровые модели местности
В настоящее время в связи с повсеместным использованием в инженерной практике методов автоматизированного проектирования, а также с внедрением геоинформационных систем в различные отрасли жизнедеятельности человека всё более широкое применение находят цифровые модели местности.
Цифровая модель местности (ЦММ) – множество, элементами которого является топографо-геодезическая информация о местности. Она включает в себя:
- метрическую информацию – геодезические пространственные координаты характерных точек рельефа и ситуации;
- синтаксическую информацию для описания связей между точками – границы зданий, лесов, пашен, водоемов, дороги, водораздельные и водосливные линии, направления скатов между характерными точками на склонах и т.п.;
- семантическую информацию, характеризующая свойства объектов – технические параметры инженерных сооружений, геологическая характеристика грунтов, данные о деревьях в лесных массивах и т.п.;
- структурная информация, описывающая связи между различными объектами – отношения объектов к какому-либо множеству: раздельные пункты железнодорожной линии, здания и сооружения населенного пункта, строения и конструкции соответствующих производств и т.п.;
- общую информацию – название участка, система координат и высот, номенклатура.
Топографическая ЦММ характеризует ситуацию и рельеф местности. Она состоит из цифровой модели рельефа местности (ЦМРМ) и цифровой модели контуров (ситуации) местности (ЦМКМ). Кроме этого ЦММ может дополняться моделью специального инженерного назначения (ЦМИН). В инженерной практике часто используют сочетание цифровых моделей, характеризующих ситуацию, рельеф, гидрологические, инженерно-геологические, технико-экономические и другие показатели.
|
|
|
ЦММ создаются с помощью таких современных программных комплексов как «AutoCad Land Development Desktop», «Autodesk Civil 3D», «Autodesk Map 3D» «MapInfo», «Pythagoras», «Credo», «GeoniCS» и др.
Цифровая модель местности, записанная на машинном носителе в определенных структурах и кодах представляет собой электронную карту.
При решении инженерно-геодезических задач на ЭВМ применяют математическую интерпретацию цифровых моделей, ее называют математической моделью местности (МММ). Автоматизированное проектирование на основе ЦММ и МММ сокращает затраты труда и времени в десятки раз по сравнению с использованием для этих целей бумажных топографических карт и планов.
Исходными данными для создания цифровых моделей местности являются результаты топографической съемки, данные о геологии и гидрографии местности.
По способу размещения исходной информации и правил ее обработки на ЭВМ цифровые модели местности делятся на регулярные, нерегулярные, структурные (рис. 34).
а) 
| б) 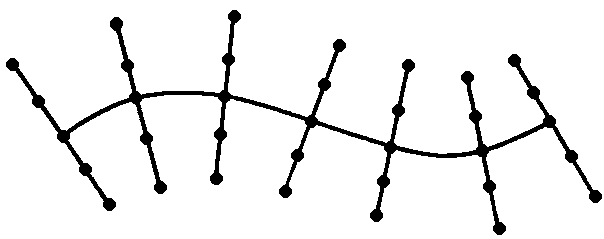 в)
в) 
| ||
г) 
| д) 
| е) 
| |
Рис. 34. Схемы цифровых моделей местности
Цифровая модель местности, в которой опорные точки с известными координатами располагаются в узлах геометрических сеток различной формы, например, в виде сети квадратов или равносторонних треугольников (рис. 34, а), называется регулярной. Используют также регулярные ЦММ на поперечниках к магистральному ходу (рис. 34, б).
Если на участок местности имеются крупномасштабные карты и планы, то создают ЦММ в виде массива точек, расположенных через определенные интервалы на горизонталях, путем перемещения визира дигитайзера по горизонтали (рис. 34, в).
|
|
|
В регулярных ЦММ геоморфология местности не учитывается, поэтому их предпочтительно использовать для равнинной местности.
Цифровая модель местности, в которой точки располагаются произвольно в пределах однородных по рельефу, геологии, гидрологии участков местности без какой-либо определенной системы, но с заданной густотой и плотностью называется нерегулярной.
Цифровая модель местности, которая состоит из точек с известными координатами, расставленных в вершинах переломов структурных (орографических) линий рельефа называется структурной.
Структурные ЦММ используют в основном для пересеченной местности. Точки структурных цифровых моделей рельефа могут располагаться:
- на основных перегибах всех структурных линий (рис. 34, г);
- в местах изменения кривизны склонов (рис. 34, д);
- вдоль скатов по линиям наибольшей крутизны в местах характерных переломов с указанием крутизны и направлений линий (рис. 34, е).
· 3.5. Задачи, решаемые на планах и картах
· 3.5.1. Определение отметок точек местности по горизонталям
· а) Точка лежит на горизонтали.
В этом случае отметка точки равна отметке горизонтали (см. рис. 35): HА = 75 м; НС = 55 м.
· б) Точка лежит на скате между горизонталями.
Если точка лежит между горизонталями, то через нее проводят кратчайшее заложение, масштабной линейкой измеряют длину отрезков а и b (см. рис. 35, точка В) и подставляют в выражение
· 
· где h – высота сечения рельефа. Если точка лежит между горизонталью и полугоризонталью, то вместо h в формулу подставляют 0,5h.
· 
· Рис. 35. Решение задач на карте с горизонталями
· 3.5.2. Определение крутизны ската
· Крутизна ската по направлению заложения определяется двумя показателями – уклоном и углом наклона по формуле
· 
· Следовательно, тангенс угла наклона линии к горизонту называется её уклоном. Уклон выражают в тысячных – промиллях (‰) или в процентах (%). Например: i = 0,020 = 20‰ = 2%.
· Для графического определения углов наклона по заданному значению заложения d, масштабу М и высоте сечения рельефа h строят график заложений (см. рис. 36).
· Вдоль прямой линии основания графика намечают точки, соответствующие значениям углов наклона. От этих точек перпендикулярно к основанию графика откладывают в масштабе карты отрезки, равные соответствующим заложениям, а именно
· 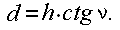
· Концы этих отрезков соединяют плавной кривой (см. рис. 36).
· Заложение линии, угол наклона которой надо определить, снимают с карты при помощи измерителя, а затем, укладывая на графике между основанием и кривой измеренный отрезок, находят соответствующее ему значение угла наклона.
· 
· Рис. 36. График заложений для углов наклона
· Аналогично строят и пользуются графиком заложений для уклонов (рис. 37).
· 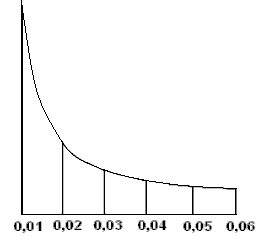
· Рис. 37. График заложений для уклонов
|
|
|


