 |
Связь между дирекционными углами предыдущей и последующей линий
|
|
|
|
На рис. 25 представлена схема определения дирекционных углов сторон теодолитного хода AB. Известен дирекционный угол исходной стороны α0 и измерены геодезическим прибором теодолитом углы β1, β2, β3, лежащие справа по ходу от А к В.
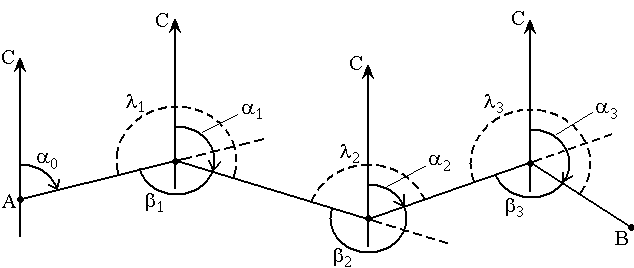
Рис. 25. Схема определения дирекционных углов сторон теодолитного хода
Найдём дирекционные углы α1, α2, α3 остальных сторон хода.
На основании зависимости между прямыми и обратными дирекционными углами можем написать:
α1 + β1 = α0 + 180° из данного выражения следует, что α1 = α0 + 180° – β1 (1).
Аналогично вычисляются дирекционные углы последующих сторон теодолитного хода:
α2 + β2 = α1 + 180° → α2 = α1 + 180° – β2 (2)
α3 + β3 = α2 + 180° → α3 = α2 + 180° – β3 (3)
...............................................................................
αn + βn = αn-1 + 180° → αn = αn-1 + 180° – βn (n)
То есть, дирекционный угол последующей стороны равен дирекционному углу предыдущей стороны плюс 180° и минус угол, лежащий справа по ходу.
Для получения контрольной формулы в выражение (2) подставим значение α1, из выражения (1)
α2 = α0 + 2 ∙ 180° – (β1 + β2).
Если продолжить аналогичные действия для последующих сторон теодолитного хода, то получим
αn = α0 + n ∙ 180° – (β1 + β2 + β3 +... + βn).
или
αn – α0 = n ∙ 180° – ∑β.
или
α0 – αn = ∑β – n ∙ 180°.
Эта формула может служить контрольной при вычислении дирекционных углов по увязанным углам β.
Если же вместо суммы исправленных углов подставить сумму измеренных углов ∑β, то та же формула позволит определить невязку fβ измеренных углов теодолитного хода, если дирекционные углы α0 и αn начальной и конечной сторон хода известны
|
|
|
fβ = ∑β – n ∙ 180° – (α0 – αn).
Иногда дирекционные углы вычисляют по углам, лежащим слева по ходу от А до В (λ1, λ2, …, λn).
β1 = 360° – λ1
β2 = 360° – λ2
........................
βn = 360° – λn
Подставим эти значения в выражения (1), (2),..., (n) получим
α1 = α0 – 180° + λ1
α2 = α1 – 180° + λ2
.................................
αn = αn-1 – 180° + λn.
Для проверки правильности вычисления дирекционных углов по углам λ, лежащим слева по ходу, используют выражения
αn – α0 = ∑λ – n ∙ 180°
или
αn – α0 = ∑λ + n ∙ 180°.
Тогда невязка fβ определяется по формуле
fβ = ∑λ + n ∙ 180° – (αn – α0).
Вопросы для самоконтроля
1. Что называется ориентированием на местности?
2. Что называется дирекционным углом линии, и в каких пределах он измеряется?
3. Что такое румб линии, и в каких пределах он измеряется?
4. Что называется истинным и магнитным азимутами?
5. Какова зависимость между дирекционным углом и истинным азимутом и между истинным азимутом и магнитным азимутом?
6. Что называется сближением меридианов?
7. Что называется склонением магнитной стрелки?
Лекция 3. Геодезическая съемка. Рельеф, его изображение на картах и планах.
Цифровые модели местности
3.1. Геодезическая съемка. План, карта, профиль
3.2. Рельеф. Основные формы рельефа
3.3. Изображение рельефа на планах и картах
3.4. Цифровые модели местности
3.5. Задачи, решаемые на планах и картах
3.6. Вопросы для самоконтроля
Геодезическая съемка. План, карта, профиль
Чтобы спроектировать линию местности на горизонтальную плоскость, нужно определить её горизонтальное проложение (проекцию линии на горизонтальную плоскость) и уменьшить его до определенного масштаба. Для проектирования на горизонтальную плоскость какого-либо многоугольника (рис. 26) измеряют расстояния между его вершинами и горизонтальные проекции его углов.
Совокупность линейных и угловых измерений на земной поверхности называется геодезической съемкой. По результатам геодезической съемки составляют план или карту.
|
|
|
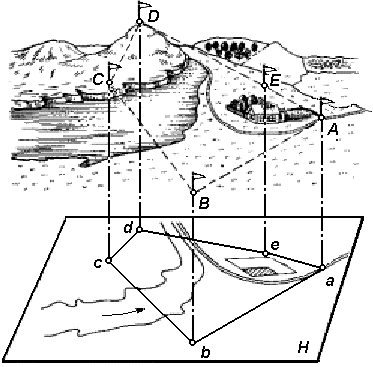
Рис. 26. Проектирование участка земной поверхности на горизонтальную плоскость
План – чертеж, на котором в уменьшенном и подобном виде изображается горизонтальная проекция небольшого участка местности.
Карта – уменьшенное и искаженное, вследствие влияния кривизны Земли, изображение горизонтальной проекции значительной части или всей земной поверхности, построенное по определенным математическим законам.
Таким образом, и план, и карта – это уменьшенные изображения земной поверхности на плоскости. Различие между ними состоит в том, что при составлении карты проектирование производят с искажениями поверхности за счет влияния кривизны Земли, на плане изображение получают практически без искажений.
В зависимости от назначения планы и карты могут быть контурные и топографические. На контурных планах и картах условными знаками изображают ситуацию, т.е. только контуры (очертания) горизонтальных проекций местных предметов (дорог, строений, пашен, лугов, лесов и т.п.).
На топографических картах и планах кроме ситуации изображают ещё рельеф местности.
Для проектирования железных, шоссейных дорог, каналов, трасс, водопроводов и других сооружений необходимо иметь вертикальный разрез или профиль местности.
Профилем местности называется чертеж, на котором изображается в уменьшенном виде сечение вертикальной плоскостью поверхности Земли по заданному направлению.
Как правило, разрез местности (рис. 27, а) представляет собой кривую линию ABC...G. На профиле (рис. 27, б) она строится в виде ломаной линии abc...g. Уровенную поверхность изображают прямой линией. Для большей наглядности вертикальные отрезки (высоты, превышения) делают крупнее, чем горизонтальные (расстояния между точками).

Рис. 27. Вертикальный разрез (а) и профиль (б) местности
|
|
|


